要は
ガウス過程を下記とかで勉強したので、そのついでにJavaScriptで実装を試みました.
誤りがあるかもしれませんので、ご指摘いただければ助かります.
(参考)下記のYoutube/Webサイト/PDF資料を参考にしています.
Youtube 【数分解説】ガウス過程(による回帰) : データのばらつきやノイズを考慮した非線形もいける回帰がしたい Gaussian Process
ガウス過程概要
ガウス過程でできること
詳しい説明は参考記事を確認ください.
簡単にいえば、ガウス過程はすでにデータが取れている複数の点と推定したい位置を使ってその点の値の範囲を分散含めて推定することができる手法と捉えています.
例えば、$y=3x$のような関係があるときに、ノイズもあったため、
$$(x,y) = (-1,-3.5), (2,6), (3, 10), (5,14)$$
なデータが取れたとします.
このとき、xが3.5や2.5、1のときにどんな値になるかを推定します.
そのとき2.5は参考になりそうなデータとしてx=2がy=6でx=3がy=10にあるため、大体$y=3x$ぐらいな関係になっていそうです.
しかし、1では、前後が-1や2で少し間があいているため、$y=3x$になっているかやや心許ないです.
その場合は、分散が大きめになっていたら良さそうです.
つまり、
- 2.5のときは、7.5±0.5ぐらい
- 1のときは、3±1ぐらい
でしょうという感じです
ガウス過程の実際の計算
実際の計算は下記のものを使用しています.データとして与えられる値を$(x_1,y_1)\dots (x_n,y_n)$として, あらかじめカーネル関数$kernel(a,b)$も決めておきます.
K = \left(
\begin{array}{cccc}
kernel(x_1, x_1) & kernel(x_1, x_2) & \ldots & kernel(x_1, x_n) \\
kernel(x_2, x_1) & kernel(x_2, x_2) & \ldots & kernel(x_2, x_n) \\
\vdots & \vdots & \ddots & \vdots \\
kernel(x_n, x_1) & kernel(x_n, x_2) & \ldots & kernel(x_n, x_n)
\end{array}
\right)
と新しい点$x_{new}$との計算.
\boldsymbol{k} = \begin{pmatrix}
kernel(x_1, x_{new})\\
kernel(x_2, x_{new})\\
\vdots\\
kernel(x_n, x_{new})
\end{pmatrix}
が用意できたら、
$$\mu = \boldsymbol{k}^T K^{-1} \boldsymbol{y}$$
によって平均が
$$\sigma = k - \boldsymbol{k}^TK^{-1}\boldsymbol{k}$$
によって分散が求まります.
これを細かく各xの座標で計算します.
やってみた
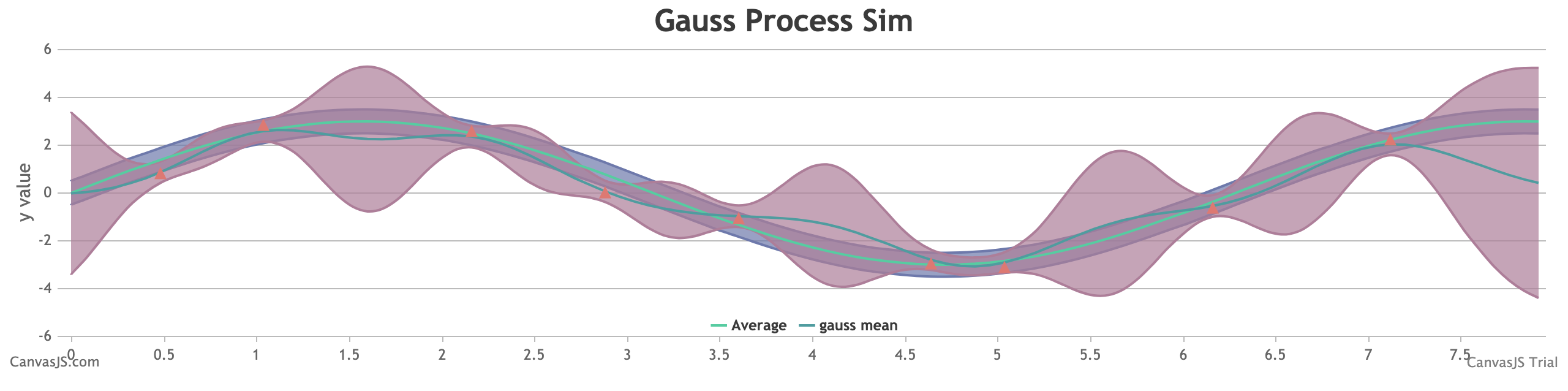
$y=sin(x)$のもとで分布を作ってみました.
こんな感じになりました.
- 使ったライブラリ
- mathjs
- 行列計算(逆行列や行列の積)のため
- canvasjs
- グラフ表示のため
全部で100点ほど計算して分布を書いていますが、データ点は、5~15ずつランダムに飛ばしながらデータをガウス分布で散らせて決めています.
コード
canvaJSのサンプルから手を入れて変えていっているので、やや汚いのは、ご了承ください.
$$y=3sin(x)$$
が実際の関数としています. これにノイズを加えたデータを取得します.
ガウス過程の計算部分
function addGaussResults(realdatas) {
let realdatasY = realdatas.map(({y})=>y);
//Calc Kernel Matrix K | カーネルKを求めます
let K = realdatas.map((data) =>
realdatas.map((data2) =>
kernel(data.x, data2.x) + NOISE_SIZE * (data.x == data2.x)
)
);
//Calc k values with new_x and Xs | ベクトル kを求めます
let ks = datas.map((data) =>
realdatas.map((realdata) =>
kernel(data.x, realdata.x)
)
);
//calc mean | 平均μを求めます. 先ほどのμを求める式より
let means = datas.map( function(data, index){
return {
x:data.x ,
y:math.multiply(math.multiply(ks[index], math.inv(K)), realdatasY)
};
});
//calc sigma | 分散σを求めます.先ほどのσを求める式より
let sigmas = datas.map( function(data, index){
return kernel(data.x, data.x) - math.multiply(math.multiply(ks[index], math.inv(K)), ks[index])
});
}
さきほどの式をそれぞれ実装下までなので、特別変わったことはありません. この式を計算するために逆行列の計算が必要で、mathjsを導入しました.
計算自体はそこまで難しくありません. 最もポピュラーなRBFカーネルに揃えたものです.
コード全体
<!DOCTYPE HTML>
<html>
<head>
<script src="https://cdnjs.cloudflare.com/ajax/libs/mathjs/9.3.2/math.min.js" integrity="sha512-vI5FJgd8TB/jorqozFDviYmt4s4j3rLDrGvGnvUh+SXql7YF+MjndWDLd/3q1Ez6Pu8exLyi2AFYerrOHqey0A==" crossorigin="anonymous"></script>
<script>
const DATA_NUM = 100;
const X_VALUE_STEP = 0.08;
const NOISE_SIZE = 0.5;
//正規分布でノイズを決める関数
function rnorm(){
return Math.sqrt(-2 * Math.log(1 - Math.random())) * Math.cos(2 * Math.PI * Math.random());
}
//ランダムなx座標のサンプルをするためだけの関数
function indexDecide(){
const MIN_STEP = 5;
const MAX_STEP_INTERVAL = 10;
return MIN_STEP + Math.floor(Math.random() * MAX_STEP_INTERVAL);
}
//カーネル関数はRBFカーネルとして、パラメータは調整して決めました.
function kernel(x1, x2){
let theta0 = 5;
let theta1 = 5;
let theta2 = 0;
return theta0 * (Math.exp(-theta1 * (x1-x2)**2 /2)) + theta2;
}
function drawLine(chart, linepoints){
chart.options.data.push(
{
type: "line",
name: "gauss mean",
showInLegend: true,
markerType: "triangle",
markerSize: 0,
dataPoints: linepoints
}
);
}
function drawArea(chart, ranges){
chart.options.data.push(
{
type: "rangeSplineArea",
markerSize: 0,
name: "gauss range",
dataPoints: ranges
}
);
}
window.onload = function () {
let datas = [];
let averages = [];
//正解の(x,y)列を求めておきます.
for(let i = 0; i < DATA_NUM; i++){
let xPos = i * X_VALUE_STEP;
let yPos = 3 * Math.sin(xPos);
let sigma = NOISE_SIZE;
datas.push({x:xPos, y:[yPos-sigma, yPos+sigma]});
averages.push({x:xPos, y:yPos});
}
var chart = new CanvasJS.Chart("chartContainer", {
theme: "light2",
title: {
text: "Gauss Process Sim"
},
axisY: {
title: "y value",
},
toolTip: {
shared: true
},
legend: {
dockInsidePlotArea: true,
cursor: "pointer",
},
data: [
{
type: "rangeSplineArea",
markerSize: 0,
name: "Sigma Range",
dataPoints: datas
},
{
type: "line",
name: "Average",
showInLegend: true,
markerType: "triangle",
markerSize: 0,
dataPoints: averages
}]
});
chart.render();
let realdatas = [];
let prevIndex = 0;
let nextIndex = indexDecide();
function addScatters() {
//データ点を決めて、realdatasに入れていきます.
//次の点は、indexDecideランダムに決めた先の値になるようにします.
for(var i = 0; i < chart.options.data[0].dataPoints.length; i++) {
if(i <= nextIndex){
continue;
}
nextIndex = indexDecide() + nextIndex;
realdatas.push({
x: chart.options.data[0].dataPoints[i].x,
y: (chart.options.data[0].dataPoints[i].y[0] + chart.options.data[0].dataPoints[i].y[1]) / 2 + rnorm() * NOISE_SIZE
});
}
chart.options.data.push({
type: "scatter",
name: "realdatas",
markerType: "triangle",
markerSize: 10,
dataPoints: realdatas
});
chart.render();
}
addScatters();
addGaussResults(realdatas);
function addGaussResults(realdatas) {
let realdatasY = realdatas.map(({y})=>y);
//Calc Kernel Matrix K
let K = realdatas.map((data) =>
realdatas.map((data2) =>
kernel(data.x, data2.x) + NOISE_SIZE * (data.x == data2.x)
)
);
//Calc k values with new_x and Xs
let ks = datas.map((data) =>
realdatas.map((realdata) =>
kernel(data.x, realdata.x)
)
);
//calc mean
let means = datas.map( function(data, index){
return {
x:data.x ,
y:math.multiply(math.multiply(ks[index], math.inv(K)), realdatasY)
};
});
//calc sigma and ranges
let sigmas = datas.map( function(data, index){
return kernel(data.x, data.x) - math.multiply(math.multiply(ks[index], math.inv(K)), ks[index])
});
let ranges = datas.map( function(data, index){
return {
x:data.x,
y:[means[index].y - sigmas[index],
means[index].y + sigmas[index]]
}
});
drawLine(chart, means);
drawArea(chart, ranges);
chart.render();
}
}
</script>
</head>
<body>
<div id="chartContainer" style="height: 300px; width: 100%;"></div>
<script src="https://canvasjs.com/assets/script/canvasjs.min.js"></script>
</body>
</html>
こちらは描画までしてみています. canvasJSでもとのsinの関数や、推定した関数、データ点などをプロットしています.
おわりに
至らぬ点、間違い等あればご指摘いただければ幸いです.