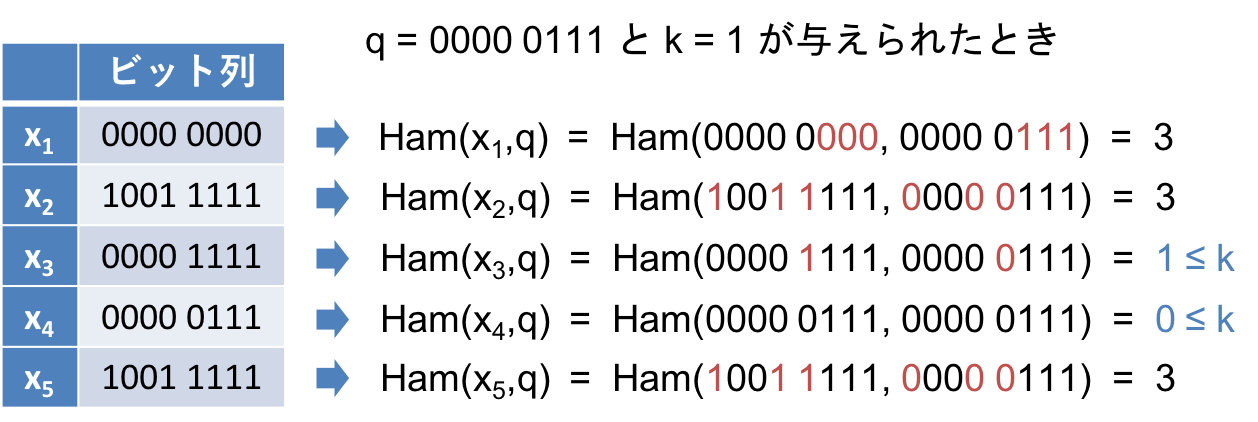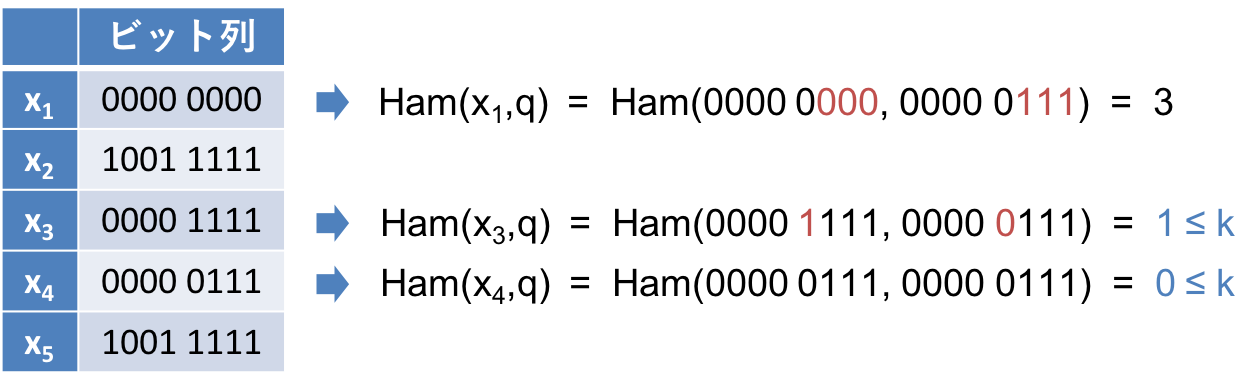お疲れ様です。真の文字列初心者、@kampersandaです。今年も恐縮ながら記事を書かせていただきます。

タイトルにあるハミング距離とは文字列間の類似度の一つで、２つの文字列間のハミング距離が小さいとき、それらの文字列は似ているとされます。実際に、たくさんある文字列の中からクエリの文字列に似た（すなわち、ハミング距離が小さい）文字列を取得したいという問題はたくさんあります。例えば、Googleは大量のWebページをSimHashとよばれるアルゴリズムを用いて長さ64のビット列に写像し、ハミング距離を用いて内容が重複するWebページを高速に検出しています。¹

本記事では、このような問題を高速に解くために広く用いられるマルチインデックスと呼ばれる手法について解説します。また、マルチインデックスを説明する上では欠かせない鳩ノ巣原理について説明します。

あと、せっかくなので最後にState-of-the-Artな内容として、今年のICDEで提案された一般鳩ノ巣原理についても簡単に紹介させてもらってます。

ハミング距離

Googleの例で示したように、よくビット列間のハミング距離を利用したいケースに遭遇します。なので、本記事でも対象をビット列に限定し、長さ $m$ のビット列 $x, y$ 間のハミング距離を以下のように定義します。

Ham(x,y)=\sum^{m}_{i=1} \left\{
\begin{array}{ll}
1 & (x[i] \neq y[i]) \\
0 & (x[i] = y[i])
\end{array}
\right.

すなわち、ビット列 $x$ と $y$ を比較して、それぞれの位置で違うビットが現れた回数が $x$ と $y$ のハミング距離です。これは、$x \oplus y$ を $x$ と $y$ に対するビット単位XOR演算、$popcnt(x)$ をビット列 $x$ に含まれる 1 の数を返す関数²だとすると、

Ham(x,y) = popcnt( x \oplus y )

により求めることができます。例えば、$x = 0101$、$y = 0110$ とすると、$0101 \oplus 0110 = 0011$ で $popcnt(0011) = 2$ なので、$x,y$ 間のハミング距離は 2 です。これは自明ですね。$x \oplus y$ の結果、$x$ と $y$ 間の異なるビットに 1 が立ちます。$popcnt$ でそれを数え上げるので、それがハミング距離になりますね。

XOR演算も $popcnt$ もビット列長 $m$ がワードサイズ（例えば 64 ビット）に線形の場合、定数時間で実行できるので、ハミング距離も定数時間で求めることが出来ます。本記事では簡単のために、ハミング距離は常に定数時間で求められるものとします。

問題設定

$n$ 個のビット列 $x_1,x_2,...,x_n$ を持っています。それぞれの長さは $m$ です。我々の目的は、クエリとして長さ $m$ のビット列 $q$ と閾値 $k$ が与えられたときに、$Ham(x_i,q) \leq k$ を満たす全ての識別子 $i$ を返すことです。

例えば、以下の例では $x_3$ と $x_4$ の $q$ とのハミング距離が $k$ 以下となるので、3 と 4 が解になります。

上の問題をどう効率的に解くかというのが本記事のテーマです。最も単純な解法は、上の例で示したように各 $x_i$ について、そのハミング距離が条件を満たすか確認していく方法です。いわゆる線形探索というやつで、この解法は $O(n)$ 時間です。残念ながら、大きなデータセットに対して適用するのは難しそうですね。

転置インデックスを用いた解法

別の解法としてよく知られる？のが、転置インデックスを用いた解法です。転置インデックスを簡単に説明すると、上の例で示したような $x_1,...,x_n$ のテーブルが識別子 $i$ によってビット列 $x_i$ にアクセスできるデータ構造だとします。これに対して転置インデックスは、ビット列 $q$ が与えられたとき $x_i = q$ となる全ての識別子 $i$ を取得できるデータ構造です。

例えば、上の例のデータセットから転置インデックスを作ると以下のようになります。このデータ構造は、例えばクエリとして $q = 1001~1111$ が与えられると、そのビット列に対応する識別子 2 と 5 を得ることができます。転置インデックスはハッシュ表などで実装すれば定数時間で検索できます。

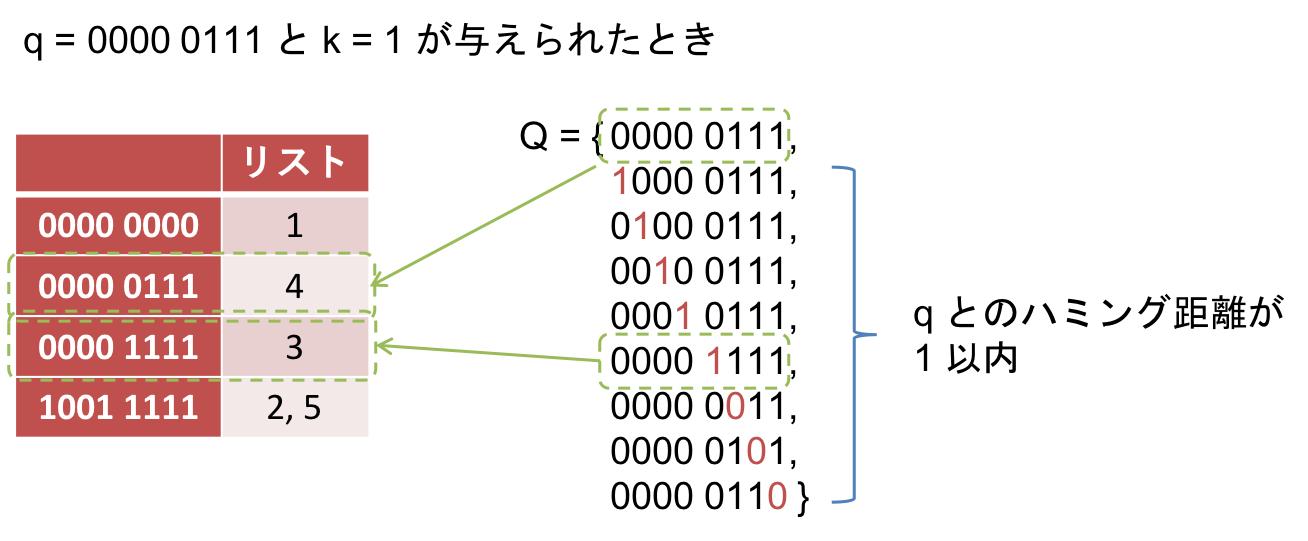
さて、この転置インデックスを使ってどのように問題を解くかというと、ビット列 $q$ と比べてハミング距離が閾値 $k$ 以下になるあらゆるビット列を生成し、それら全てに対して検索するだけです。もう少しちゃんと書くと、以下のようなビット列集合 $Q$ を生成し、各 $q \in Q$ をクエリとして検索することで、得られた識別子の集合が解になります。

Q = \left\{ q' \in \{0,1\}^m ; Ham(q,q') \leq k \right\}

例えば、上で作った転置インデックスに対し、クエリ $q = 0000~0111$、$k=1$ を解くと以下のようになります。このとき、$0000~0111$ と $0000~1111$ が検索に掛かり、得られた識別子 3 と 4 が解になります。最初に示した線形探索の例と同じ解が得られていることがわかります。

問題点

多くの方が、上の例でクエリとして 9 個ビット列が生成されたことに嫌な予感がしたと思います。そうです。この解法の問題点は、ビット列長 $m$ や閾値 $k$ が大きい場合に生成されるクエリ集合 $Q$ が膨大になることです。実は、$Q$ のサイズは以下の式で求められます。

\sum^{k}_{r=0}\binom{m}{r}

二項係数が出てきたということは、結構なでかさになり得るということです。イメージが湧きづらい人のために、$m = 64$ のときに $k$ を大きくすると $Q$ のサイズが実際にどれくらいになるのかを（Pythonが）頑張って調べたので列挙します。

$k$	$Q$ のサイズ
0	1
1	64
2	2,079
3	43,742
4	679,117
5	8,303,629
6	83,277,996
7	704,494,187
8	5,130,659,554
9	32,671,244,065
10	184,144,458,880
11	927,740,240,703
12	4,211,954,943,758
13	17,348,813,755,981
14	65,204,513,714,796
15	224,723,513,577,515
16	713,250,450,657,094
17	2,092,620,625,940,610
18	5,694,309,416,958,690
19	14,414,187,542,581,400
20	34,033,913,325,232,500
21	75,141,910,203,168,200
22	155,489,358,646,406,000
23	302,210,786,238,405,000
24	552,859,891,708,071,000
25	953,898,460,459,537,000
26	1,555,456,313,586,730,000
27	2,402,093,292,062,050,000
28	3,520,863,585,047,290,000
29	4,909,681,879,787,590,000
30	6,529,969,890,317,930,000

見ての通り地獄です。$k = 30$ で六百五十二京九千九百六十九兆八千九百三億千七百九十三万（ろっぴゃくごじゅうにけいきゅうせんきゅうひゃくろくじゅうきゅうちょうはっせんきゅうひゃくさんおくせんななひゃくきゅうじゅうさんまん）になります。³ ⁴

そもそも、線形探索より高速に検索することが目的でしたので、$Q$ のサイズがデータの個数 $n$ を上回っては元も子もないのです。例えば $n$ が10億でも、$k = 8$ で $Q$ のサイズは $n$ をあっけなく上回ります。

でもまぁ安心してください。「だから皆さん線形探索を使いましょう！」なんてオチではないですし、まだ鳩も出てきてないです。以下では、この転置インデックスを用いた解法を上手く活用し、高速に問題を解くマルチインデックスという手法を紹介します。

マルチインデックス

ここからは、転置インデックスによる解法を大きいパラメータに対しても有効に使うために用いられるマルチインデックスという手法を紹介していきます。マルチインデックスは、その名の通り複数のインデックスを作る手法です。構築段階と検索段階に分けて、具体的にそのアプローチを見ていきましょう。

構築

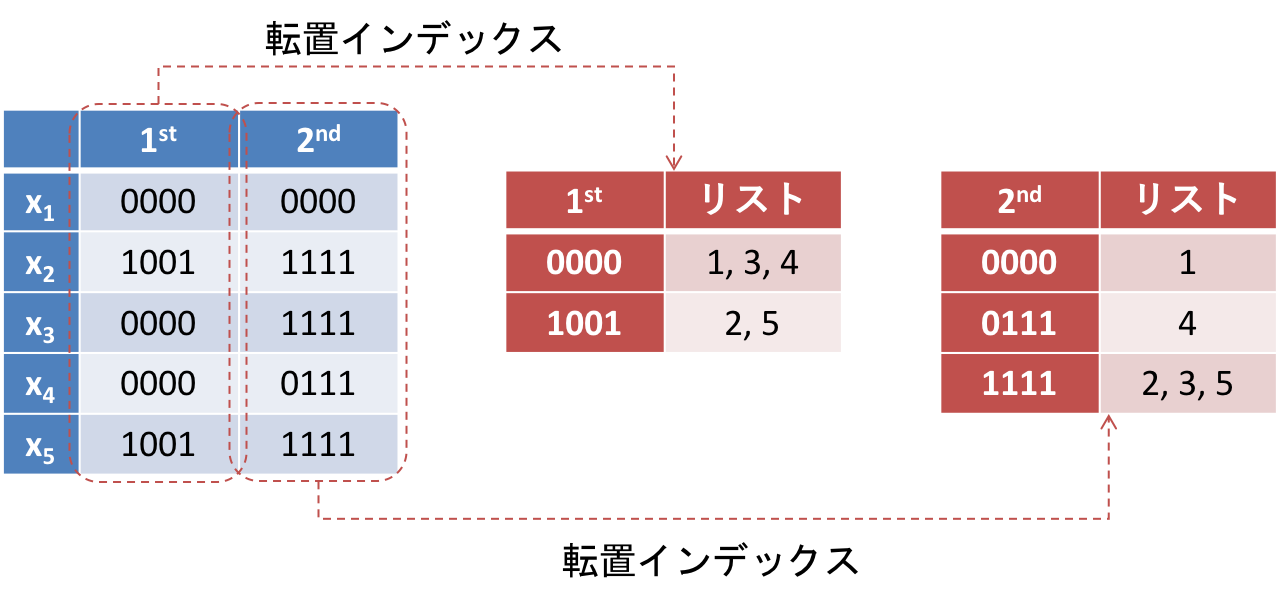
マルチインデックスでは、まず各ビット列 $x_i$ を $b$ 個の互いに疎なブロックに分割します。本記事では、$j$ 番目のブロックを $x_i^j$ と記述します。例えば、$x_2 = 1001~1111$ を $b = 2$ 個のブロックに分割する場合、真ん中で $x_2^1 = 1001$ と $x_2^2 = 1111$ に分割できます。このとき、互いに疎であればどのように分割してもいいのですが、今回は簡単のために各ブロックのサイズが均等になるように真ん中で分割します。$x_2$ を真ん中で分けたのと同じように、他のビット列も分割すると、下の図のように１つ目のブロックと２つ目のブロックからそれぞれ構成されるビット列の系列が得られます。

後は、それぞれのブロックに対して、同じように転置インデックスを構築するだけです。今回の例では、図のように２つの転置インデックスが構築されます。

検索

マルチインデックスでは、これらの複数の転置インデックスに対し検索を実行します。このとき、Filter-and-Verification戦略⁵というものに基づいて解を求めます。この戦略は、FilterステップとVerificationステップの二段階に分かれます。

Filterステップ

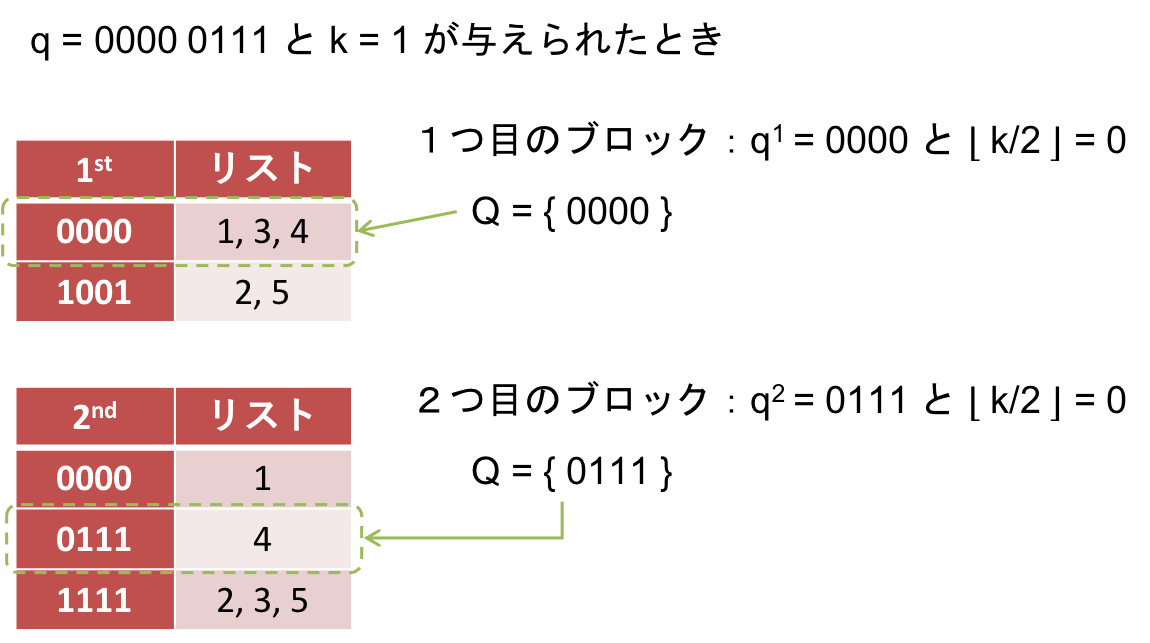
クエリとしてビット列 $q$ と閾値 $k$ が与えられたときに、Filterステップではビット列 $x_i$ を分割したのと同じように $q$ も $b$ 個のブロック $q^1,...,q^b$ に分割します。そして各 $j = 1, ..., b$ に対し、ビット列 $q^j$ と閾値 $\lfloor k/b \rfloor$ を用いて、$j$ 番目の転置インデックスを検索し解候補を得ます。この段階では、あくまで解候補であり解ではないことに注意してください。また、閾値として $\lfloor k/b \rfloor$ を用いることに謎が残りますが、これは後で説明します。ここでは、小さい閾値で検索できて嬉しいな程度に思っててください。

例えば、これまでと同じようにビット列 $q = 0000~0111$、閾値 $k=1$ を解くと、以下の図ように $q$ を $q^1 = 0000$ と $q^2 = 0111$ に分けます。また、各ブロックに割り当てる閾値は $\lfloor k/2 \rfloor = 0$ になります。これらを用いて各インデックスに対し検索すると、閾値が 0 なので各 $Q$ のサイズは 1 になります。分割しなかった場合と比べて、検索しなければならないビット列の数が 9 から 2 に削減されているのがわかります。結果として、１つ目のインデックスからは {1,3,4}、２つ目のインデックスからは {4} が解候補として得られます。これらを結合した結果、解候補として {1,3,4} が得られたことになります。

Verificationステップ

Verificationステップは読んで字のごとくです。先程得られた解候補に対して実際にクエリとのハミング距離を計算し検証することで真の解を見つけます。

上の例では解候補として {1,3,4} が得られたので、クエリビット列 $q = 0000~0111$ と $x_1,x_3,x_4$ とのハミング距離が実際に閾値 $k=1$ 以下かを調べます。すると、以下の図のように $x_1$ は解ではないことがわかり、3 と 4 が解として得られます。これは今までの例で得られた結果とめでたく一致します。

閾値の設定条件

マルチインデックス。聞いてみればえらくあっさりとした内容だったと思います。でもまだ棚上げしてることが一つ残ってますよね。そうです。各ブロックに対する閾値として割り当てられた $\lfloor k/b \rfloor$ です。果たして解候補を得るために $\lfloor k/b \rfloor$ は適した値だったのでしょうか。

ここで改めて各ブロックに割り当てる閾値に求められる要件を考えてみると、以下の２つになります。

この閾値を用いて得られる解候補が真の解を全て含んでいること。
高速に検索するためや解候補を少なくするために小さな閾値であること。

とりわけ１つ目の要件は重要です。例えば、上の例で得られた解候補が {1,3} で 4 が含まれてなかったとすれば、Verificationステップでいくら頑張ろうとも真の解を得ることができません。このように真の解を見逃すことを、False Negativeといいます。一方で、1 のような解ではないものが含まれてる分には、Verificationステップで検出できるので（最終的に真の解が得られるという点では）問題ありません。このような誤検出をFalse Positiveといいます。

改めて、閾値の設定条件はFalse Negativeを許してはいけないということです。$\lfloor k/b \rfloor$ は小さな閾値を用いるという点では良さそうですが、False Negativeは本当に起こらないのでしょうか？実はこれは鳩ノ巣原理により簡単に証明することができます。

鳩ノ巣原理（Pigeonhole Principle）

てことでようやく鳩ノ巣原理について解説します。といっても簡単な原理ですし、調べればいろんな応用が出てくると思います。

鳩ノ巣原理はいろんな説明の仕方があると思いますが、今回のシナリオに沿って説明すると以下のような原理になります。

【鳩ノ巣原理】
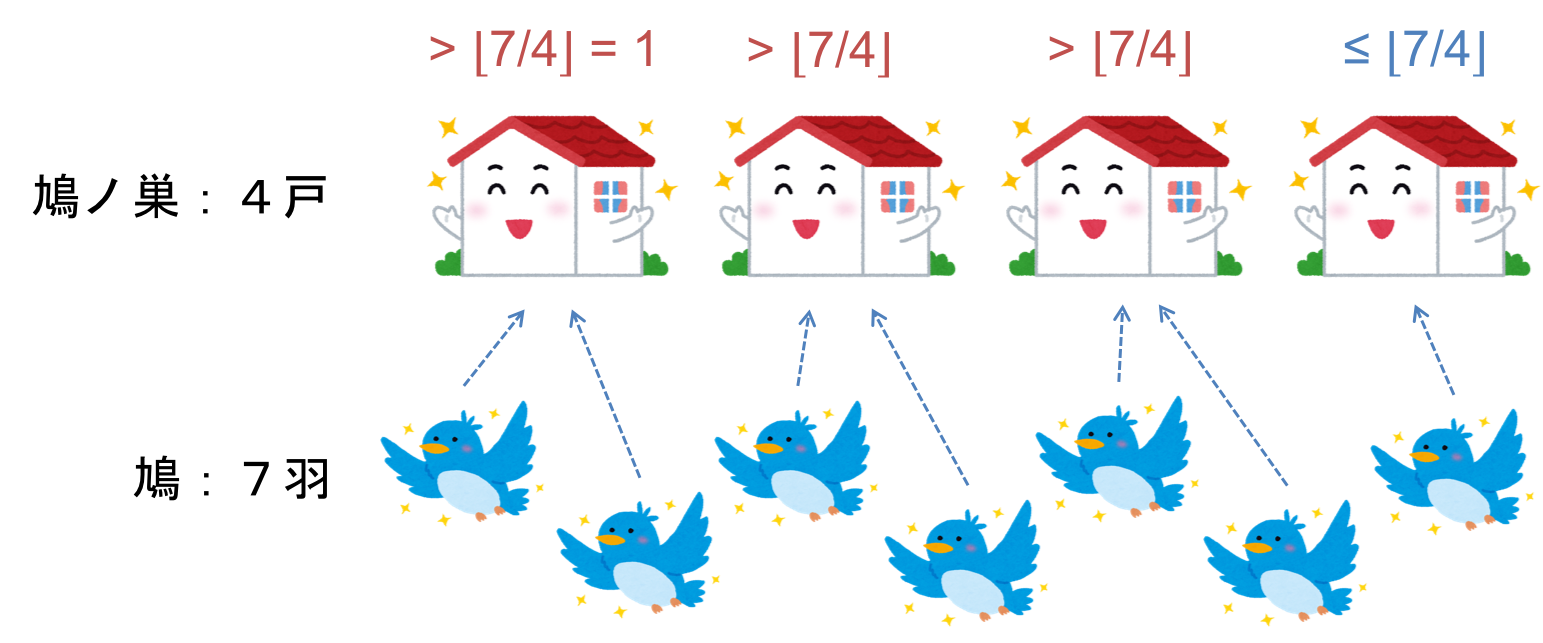
$M$羽の鳩が$N$個の鳩ノ巣に割り振られているとき、$\lfloor M / N \rfloor $羽以下の鳩を含む巣が少なくとも１つ存在する。

例えば、$M=7$、$N=4$ の場合を考えてみます。以下の図のように７羽の鳩をとりあえず均等に割り振ってみます。すると、一番右の巣に割り振られた鳩が１羽となり、$\lfloor 7 / 4 \rfloor = 1$ 以下となります。他の割り振り方を考えてみても、必ず一つの巣は $\lfloor 7 / 4 \rfloor$ 羽以下になるはずです。

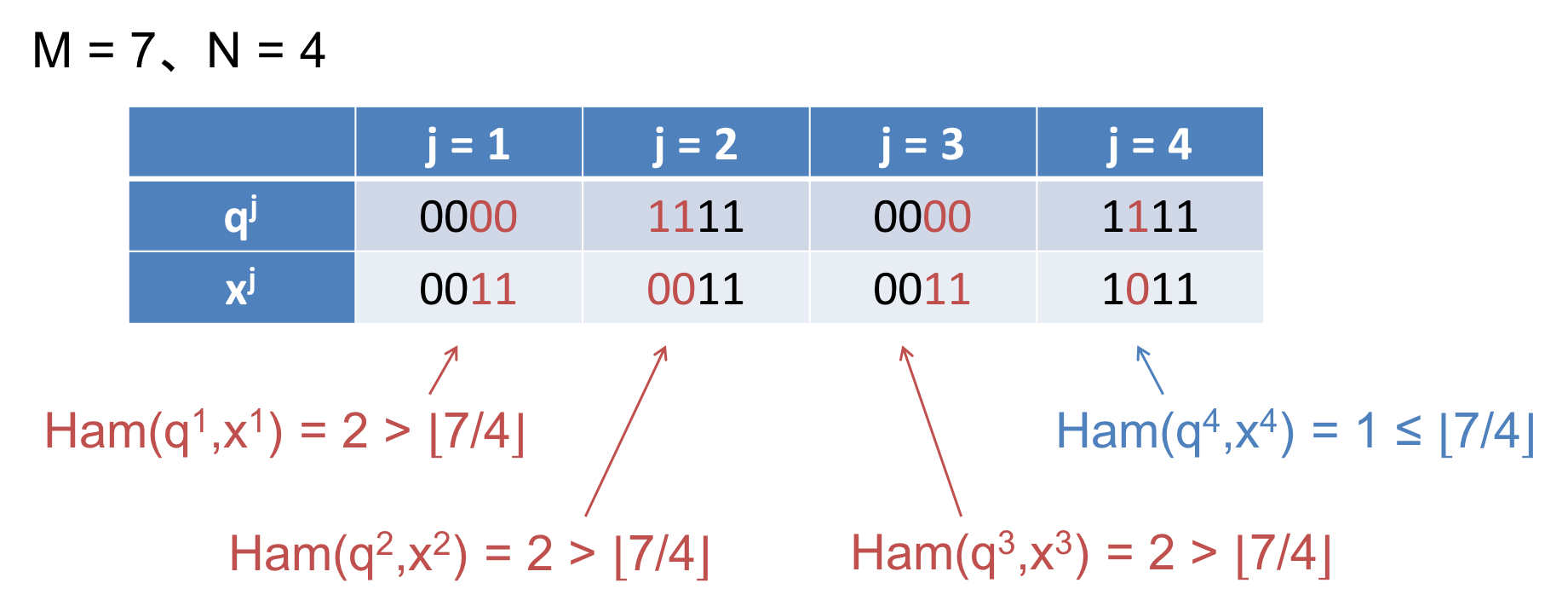
実はこの鳩と鳩ノ巣の関係は、ビット列間の不一致文字とブロックの関係に置き換えることができます。例えば、以下の図のように $b=4$ つのブロックに分割されたビット列 $q$ と $x$ のハミング距離を考えます。以下のハミング距離は $Ham(q,x) = 7$ ですが、これは７つの不一致文字が４つのブロックに割り振られているとも考えられます。すなわち、鳩ノ巣原理における $M = 7$、$N = 4$ です。これは、ハミング距離が $\lfloor M / N \rfloor = \lfloor 7 / 4 \rfloor = 1$ 以下となるブロックが少なくとも１つは存在するということを保証します。

以上のことから、ブロック数 $b$ のマルチインデックスにおいて検索をしたとき、クエリビット列 $q$ とのハミング距離が $k$ 以下である $x_i$ について、少なくともハミング距離が $\lfloor k / b \rfloor$ 以下となるブロックが１つは含まれることが保証されます。

よって、マルチインデックスの閾値として $\lfloor k / b \rfloor$ を用いたときFalse Negativeが起きないことが証明されました。めでたいです。

一般鳩ノ巣原理（General Pigeonhole Principle）

おかげさまで基本的なことは一通り言い終わったのですが、せっかくなのでState-of-the-Artなことも書こうと思います。

マルチインデックスは非常に実用的な手法で、今までにいくつかの亜種が発表されてますが、ずっとそれらは鳩ノ巣原理に基づいて設計されてきました。しかし、False Negativeを起こらないようにするとき、$\lfloor k / b \rfloor$ という閾値は本当に小さい値なのでしょうか？もしこれ以上に小さい閾値の割り当てが存在するなら、今まで以上にインデックスを高速に検索でき、解候補も少なくて済みます。

実は今年のICDEというデータベース系の有名会議で、一般鳩ノ巣原理（General Pigeonhole Principle）⁶が提案され、従来の鳩ノ巣原理に基づく割り当てより小さい閾値の割り当てが存在し、且つ一般鳩ノ巣原理に基づく割り当てより小さい閾値の割り当てが他に存在しないことが示されました。

Jianbin Qin, Yaoshu Wang, Chuan Xiao, Wei Wang, Xuemin Lin, and Yoshiharu Ishikawa, "GPH: Similarity Search in Hamming Space", 34th International Conference on Data Engineering (ICDE), pp. 29-40, 2018.

恐縮ながら、簡単に解説させていただきます。ただし本当は、これを議論する上で「小さい閾値の割り当てとは何か」を論文に従ってちゃんと定義する必要があります。でもちょっと長くなるし面倒なので、今回はその辺を端折って一般鳩ノ巣原理を示し、分かりやすい一例を示すだけに留めたいと思います。

また、一般鳩ノ巣原理との違いを明らかにするため、以下ではこれまで説明した従来の鳩ノ巣原理を基本鳩ノ巣原理とよびます。

【定理：基本鳩ノ巣原理】
互いに疎な $b$ 個のブロックに分割された２つのビット列 $q = q^1,...,q^b$ と $x = x^1,...,x^b$ が与えられたとき、$\lfloor k / b \rfloor$ を閾値として各ブロックに割り当てる。もし $Ham(q,x) \leq k$ なら、$Ham(q^j,x^j) \leq \lfloor k / b \rfloor$ を満たすブロック $j$ が少なくとも１つは存在する。

補題

まずは準備として柔軟鳩ノ巣原理（Flexible Pigeonhole Principle）⁷を導入します。基本鳩ノ巣原理では、どのブロックにも同じ閾値を割り当ててました。この補題では、各ブロックの閾値の合計値がある基準を満たしていれば、柔軟に違う閾値を割り当ててもFalse Negativeが起こらないことを証明します。

【補題１：柔軟鳩ノ巣原理】
互いに疎な $b$ 個のブロックに分割された２つのビット列 $q = q^1,...,q^b$ と $x = x^1,...,x^b$ が与えられたとき、$\sum_{1\leq j \leq b} k^j = k$ となるような整数値の閾値 $k^1,...,k^b$ をそれぞれのブロックに割り当てる。もし $Ham(q,x) \leq k$ なら、$Ham(q^j,x^j) \leq k^j$ となるようなブロック $j$ が少なくとも１つは存在する。

改めて確認しておくと、「$Ham(q^j,x^j) \leq k^j$ となるようなブロック $j$ が少なくとも１つは存在する」ことが、マルチインデックスにその $k^j$ を閾値として用いるとFalse Negativeが必ず起こらないことを保証しています。

この補題は背理法を使って簡単に証明できます。

（証明）
$Ham(q^j,x^j) \leq k^j$ となるようなブロックが１つも存在しないことを仮定する。$b$ 個のブロックは互いに疎なので $Ham(q,x)=\sum_{1\leq j \leq b} Ham(q^j,x^j)$ が成り立つが、仮定より $\sum_{1\leq j \leq b} Ham(q^j,x^j) > k$ が成り立つので、矛盾が生じる。

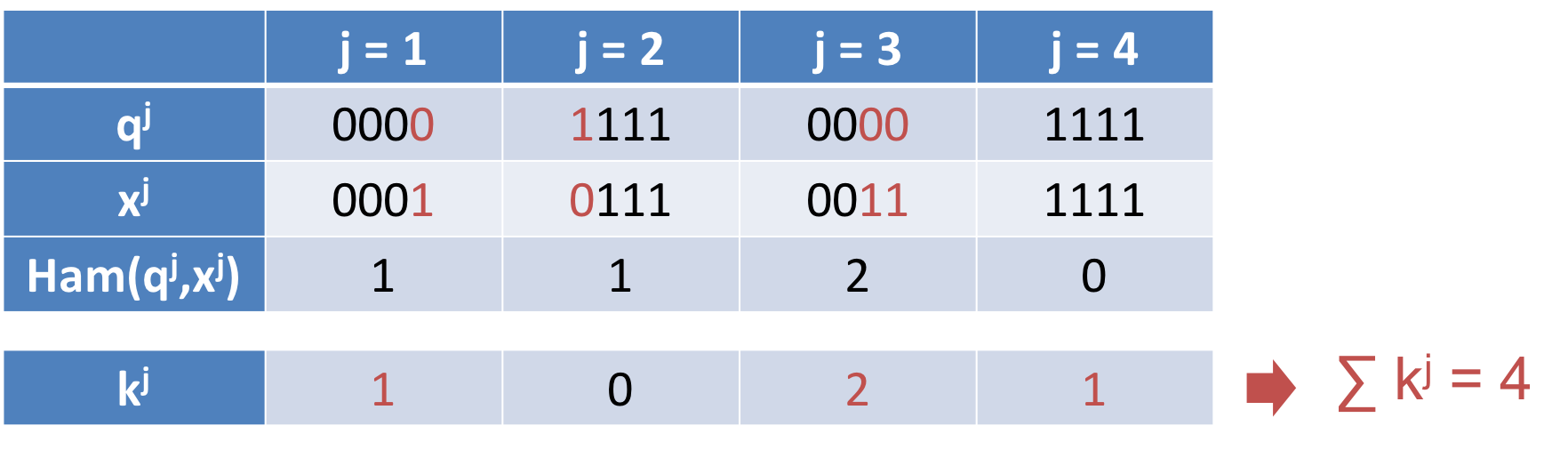
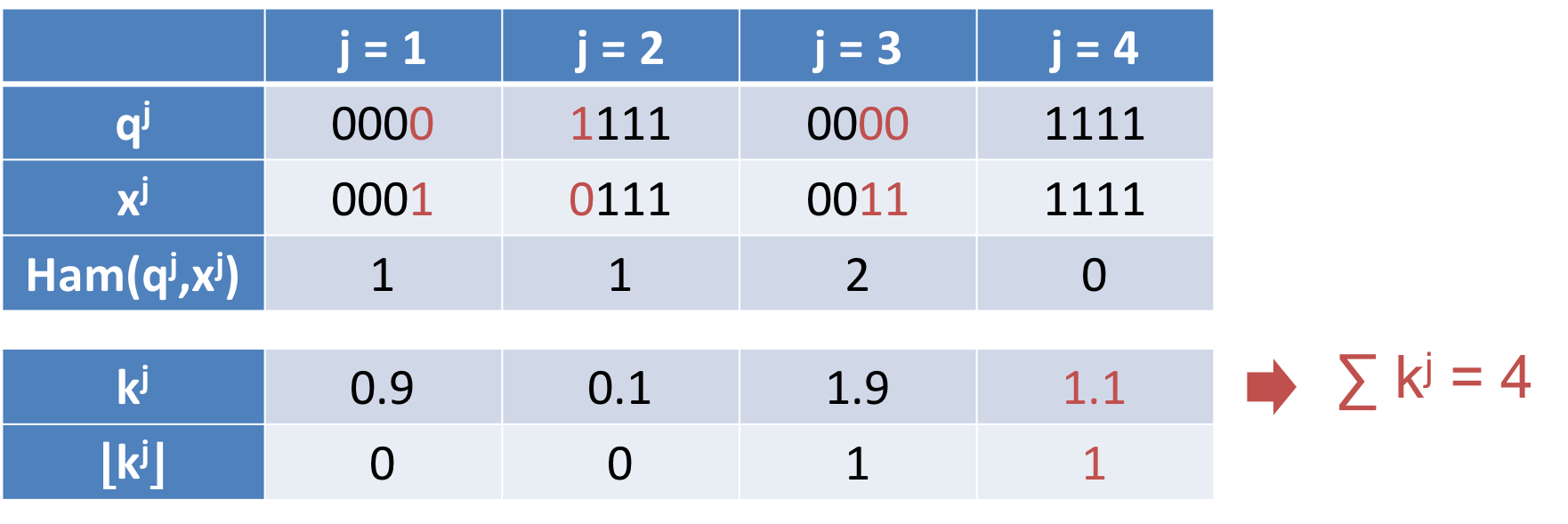
例えば、以下のように $Ham(q,x) = 4$ のとき、合計が 4 になるように閾値 $k^j$ を割り当てると、少なくとも１つは$Ham(q^j,x^j) \leq k^j$ となるようなブロックが存在します。この例では、１番目と３番目と４番目のブロックがそうです。

この補題の面白いところは、実は整数値に限らず実数値を閾値に割り当てても補題が成り立つところにあります。すなわち、以下のような補題も成り立ちます。

【補題２：柔軟鳩ノ巣原理（実数値版）】
互いに疎な $b$ 個のブロックに分割された２つのビット列 $q = q^1,...,q^b$ と $x = x^1,...,x^b$ が与えられたとき、$\sum_{1\leq j \leq b} k^j = k$ となるような実数値の閾値 $k^1,...,k^b$ をそれぞれのブロックに割り当てる。もし $Ham(q,x) \leq k$ なら、$Ham(q^j,x^j) \leq k^j$ となるようなブロック $j$ が少なくとも１つは存在する。

これは同じように背理法で証明できるので、証明は省略します。

一見、補題１と補題２の違いは「整数値」と「実数値」だけのように思えますが、実は暗に大きく変わってるところがあります。それは

$Ham(q^j,x^j) \leq k^j$ となるようなブロック $j$ が少なくとも１つは存在する。

という部分です。今回のケースにおいて、$k^j$ は実数値なのですがハミング距離は整数値です。故に以下のように解釈することができます。

$Ham(q^j,x^j) \leq \lfloor k^j \rfloor$ となるようなブロック $j$ が少なくとも１つは存在する。

すなわち、小数点以下を切り捨てることで、補題１と $k^j$ の合計値は同じでも、より小さい閾値で検索できるようになります。

例えば、先程の例に対して、以下のように実数値の閾値を割り当てることができます。閾値の合計値は同じく 4 です。しかし、小数点以下を切り捨てられるので、実質 $\lfloor k^j \rfloor$ を割り当てていることになります。先程の例と比べて、小さな閾値が割り当てられてるのがわかります。それでも、$Ham(q^j,x^j) \leq \lfloor k^j \rfloor$ となるようなブロックは必ず存在します。この例では、一番右です。

定理

準備も整ったので、一般鳩ノ巣原理を以下に示します。

【定理：一般鳩ノ巣原理】
互いに疎な $b$ 個のブロックに分割された２つのビット列 $q = q^1,...,q^b$ と $x = x^1,...,x^b$ が与えられたとき、$\sum_{1\leq j \leq b} k^j = k - b + 1$ となるような整数値の閾値 $k^1,...,k^b$ をそれぞれのブロックに割り当てる。もし $Ham(q,x) \leq k$ なら、$Ham(q^j,x^j) \leq k^j$ となるようなブロック $j$ が少なくとも１つは存在する。

証明

一般鳩ノ巣原理は上記の補題を用いて証明できます。

まず、$\sum_{1\leq j \leq b} k^j = k - b + 1$ となるような整数値の閾値 $k^1,...,k^b$ を考えます。以下の図のように、$k^1,...,k^{b-1}$ にそれぞれ 1 を加算することで得られる $k'^1, ..., k'^{b-1}$ と $k'^b = k^b$ を考えると、$k'^j$ の合計は $k$ なので補題１より閾値 $k'^j$ ではFalse Negativeが起こらないことが保証されます。

続いて以下の図のように、ものすごく小さい実数値 $\varepsilon > 0$ を $k'^1,...,k'^{b-1}$ から引くことで得られる $k''^1,...,k''^{b-1}$ と、$k'^b$ に $(b-1)\varepsilon$ を足して得られる $k''^b$ を考えると、その合計は変わらず $k$ であり、$k''^j$ は実数値なので補題２より閾値 $k''^j$ ではFalse Negativeが起こらないことが保証されます。

そして、補題２のときと同じように、$k''^j$ の小数点以下も切り捨てることができます。その結果、もとの $k^j$ が得られるので、$\sum_{1\leq j \leq b} k^j = k - b + 1$ となるような整数値の閾値 $k^j$ ではFalse Negativeが起こらないことが保証されます。

よって、一般鳩ノ巣原理が証明されました。めでたしめでたし。

例

本当は「めでたしめでたし」ではなく、一般鳩ノ巣原理に基づく閾値の割り当てよりも他に小さい割り当てが存在しないことや、基本鳩ノ巣原理より大きくならないことを示さないといけないのですが、それは論文参照でお願いします。

ここでは最後に、この割り当てが基本鳩ノ巣原理の割り当てより小さくなってる一例を示します。

例えば、$k=4, b=4$ の場合を考えますと、基本鳩ノ巣原理に基づけば、$\lfloor k / b \rfloor = \lfloor 4/4 \rfloor = 1$ が各ブロックの閾値になります。しかし、一般鳩ノ巣原理に基づけば、$k-b+1 = 4 - 4 + 1 = 1$ より、$k^1 = 0, k^2 = 0,k^3 = 0,k^4 = 1$ のように閾値を割り振ることができます。この例において、一般鳩ノ巣原理が基本鳩ノ巣原理より嬉しいのは明らかですね。

おわりに

というわけで、重要なことを論文に投げた形で本記事は終わります。完全なる体力切れです。すみません。でもいっぱい図を作ったんで許してください。

もしここまで読んでくれた方いらっしゃいましたら、ありがとうございました。

マルチインデックスに関して、~~残念ながら問い合わせ時間に関する理論的な解析などを僕は確認できてないのですが~~、非常に実用的な手法なので、もし今回設定したような問題を解きたい方にはオススメします。
追記：嘘です。「Fast search in hamming space with multi-index hashing, CVPR2012」あたりを読めば幸せになれます。

一般鳩ノ巣原理の論文については、この他にもビット列中の1と0の出現に偏りがあった場合の適した閾値の割り振り方なども提案しているので、興味がある方は読んでみてはいかがでしょうか。あと今回は特に触れませんでしたが、一般鳩ノ巣原理は閾値を非負整数に制限していません。すなわち、負の値も閾値として設定できるということです。偏りに応じた割り振りでは、この辺りの特性も考慮したりしていて面白いです。

あと、これの他にPigeonring Principle⁸とかもあったりします。これも面白いです。てか凄いです。

Gurmeet Singh Manku, Arvind Jain, and Anish Das Sarma, "Detecting near-duplicates for web crawling", 16th International Conference on World Wide Web (WWW), pp. 141–150, 2007. ↩
$popcnt$についてはpopcountで調べればいろんな記事がヒットすると思います。例えば、http://www.nminoru.jp/~nminoru/programming/bitcount.html ↩
インパクトを演出するために $k = 30$ まで示しましたが、こんな大きな閾値で実際に検索したいかは別の話です。 ↩
どうでもいいことですが、以下のサイトで数字から漢数字に変換しました。https://www.sljfaq.org/cgi/numbers_ja.cgi ↩
他にも、「Filter-and-Refine」や「Search-and-Check」とよばれたりしてます。 ↩
勝手に直訳してます。一般化鳩ノ巣原理にすべきだったでしょうか。 ↩
これも勝手に直訳してます。もっとセンスの良いのがありそうですが。 ↩
Jianbin Qin and Chuan Xiao, "Pigeonring: A Principle for Faster Thresholded Similarity Search", 44th International Conference on Very Large Data Bases (VLDB), pp. 28–42, 2018. ↩

ハミング距離と鳩ノ巣原理