こんにちは!
BrainPad Advent Calender 2023 11日目担当のkamoです。
今年は11/19に実施された統計検定1級を受験してきました。
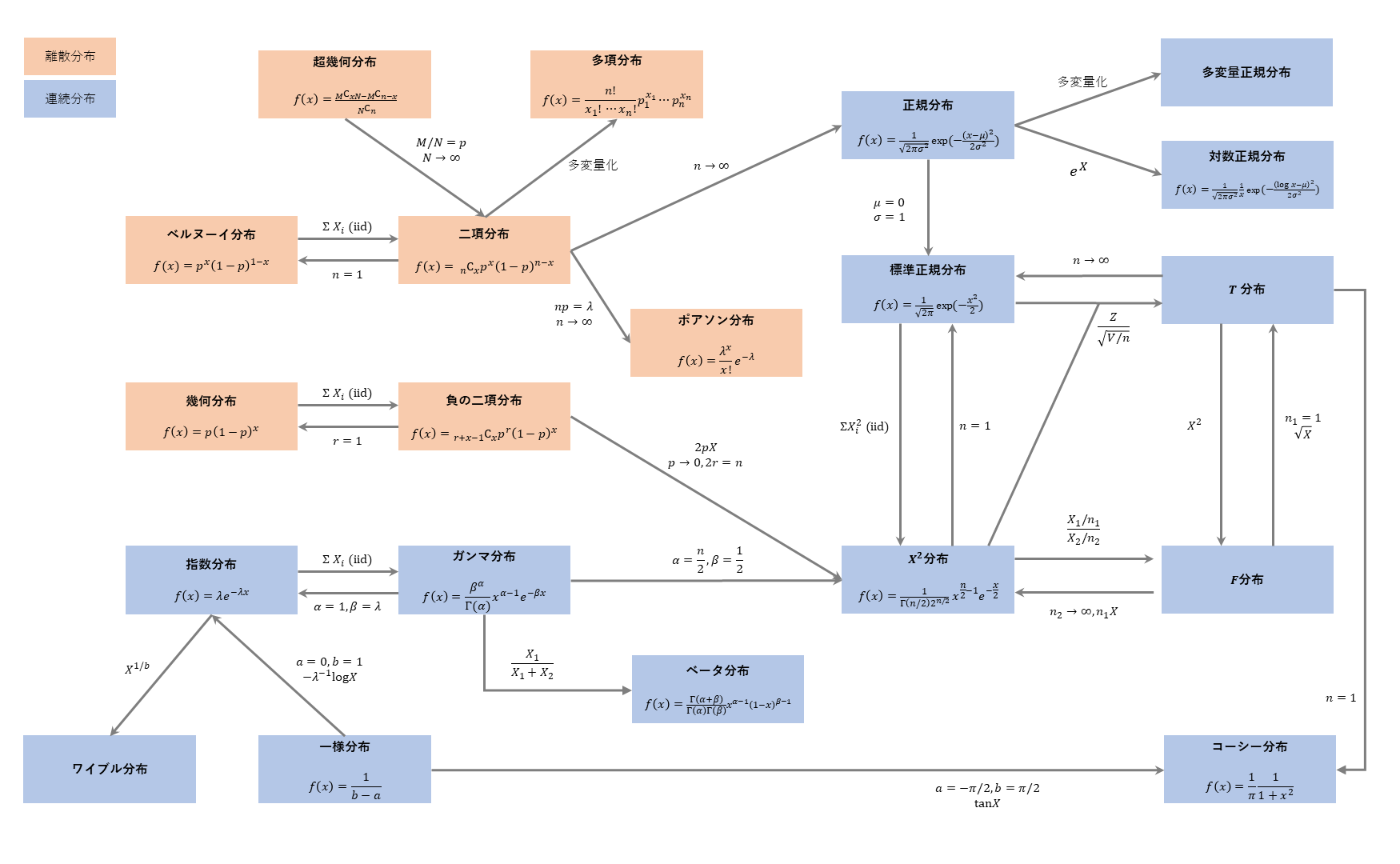
統計検定1級の有名な勉強法として、確率分布曼荼羅(まんだら) を作るというものがあります。
本記事ではその曼荼羅の1サンプルとして、私が作成したものを紹介させていただきます。
来年以降、統計検定1級を受けられる方々(自分も含みうる)の参考になれば幸いです。
何度かチェックはしましたが、ミスがあるかもしれません。間違いにお気づきの際はご指摘いただけると幸いです。
確率分布曼荼羅とは
確率分布曼荼羅は、要するに確率分布同士の関係性をまとめた図のことを指しています。
統計検定1級では確率分布に精通していることが求められるのですが、その対策として曼荼羅作るという勉強方法が有名であり、多くの方が自分なりの曼荼羅を作りながら勉強しています。(おそらく)
広く認知されている理由は、けんちょんさんが 「統計検定 1 級に合格する方法」という記事で紹介してくださっているためではないかと推測しています。実際に非常によい勉強になりました。
公式なものではUnivariate Distribution Relationshipsの図も有名で、こちらを参考にされる方も多いかと思います。この図は 著者自身のwebページ でも公開されており、ポインタを合わせるとインタラクティブに図を見たり、分布の詳細ページに飛ぶことができるので非常に楽しいページです。
確率分布曼荼羅作ってみた
ということで、私が作成した曼荼羅がこちらです。
実際に勉強する上では、さらにいろいろな関係性を書き込んでいましたが、今回は私が整理する上で骨格にしていた関係性になるべく絞り込んで作成しています。
- 一級の出題範囲に記載されている分布は概ね網羅されていますが、一部(離散一様分布やロジスティック分布など)記載されていない分布もあります。
- パラメータが定義揺れする分布もあるため質量関数と密度関数をなるべく記載しましたが、複雑なものは省略しています。悪しからず。
イメージとしては
- ベルヌーイ、二項分布から正規・ポアソンへ分岐する流れ
- 指数分布(幾何分布)からχ二乗分布への流れ
- 標準正規分布から派生する分布の関係性(χ二乗分布, T分布, F分布)
の3つを軸として、さらにそれらの関係性や枝葉の派生を抑えていくように整理をしていました。
以下、いくつか雑多ではありますが、整理観点のようなものを挙げてみます。
独断と偏見による整理観点
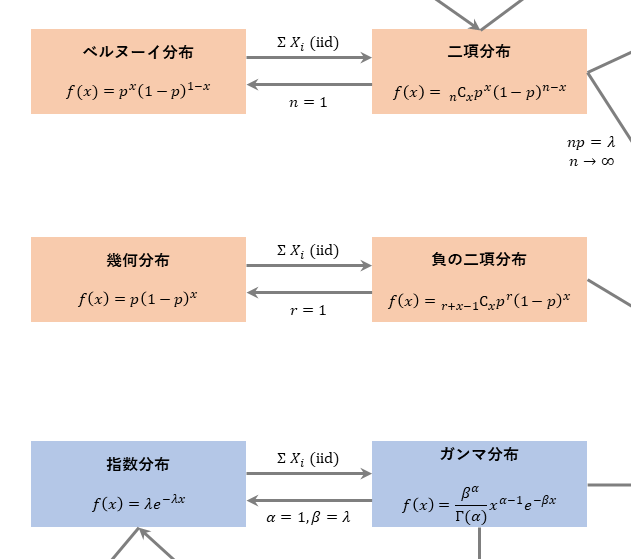
独立同一分布の足し合わせの関係
個人的には、ここを軸とすると様々な関係の土台になるため、 最初に抑える点としておすすめです。
独立にベルヌーイ分布に従う確率変数を足し合わせると二項分布になることは、具体例がわかりやすいことからも有名ですが、統計検定1級の範囲では同様の関係があと2組存在します。
1つは幾何分布と負の二項分布、もう一つは指数分布とガンマ分布です。(私の曼荼羅では、これらが3つ並ぶ形で作られています。)
特に幾何分布と指数分布、負の二項分布とガンマ分布は離散、連続の関係となっております。
また、この関係を抑えていると、過去問で頻出の平均、分散、確率(モーメント)母関数の整理に非常に役立ちます。
例えば、ガンマ分布の期待値は、指数分布の期待値である $1/λ=1/β$ を $α$ 倍した($α$個足し合わせた)ものなので、$α/β$となります。独立なので、分散も素直に和をとることができ、$1/λ^2$から$α/β^2$となることが分かります。モーメント母関数も指数分布のものを$α$乗するとガンマ分布になります。
ガンマ分布の$β$は逆数の形で定義されている書籍もありますが、個人的には指数分布の$λ$とそのまま対応するもの、つまり期待値が$α/β$になる形で記憶していました。
個人的に、負の二項分布とガンマ分布はあまりなじみがなかったため、この性質に出会ってから非常に見通しが良くなりました。
再生性を持つ分布
再生性を持つ分布としてまず思い浮かぶのは正規分布とポアソン分布だと思うのですが(個人の意見です)、それ以外はあまり頭に残りにくいなと感じておりました。
特に負の二項分布やガンマ分布は片方のパラメータだけが再生性を持ち、初見だと正直美しくないと感じる方も多いのではないでしょうか。
ここで「独立同一分布の足し合わせの関係」を踏まえると、負の二項分布は幾何分布の、ガンマ分布は指数分布の確率変数を足し合わせたもののため、足し合わせる個数に対応するパラメータ(それぞれrとα)について再生性が成り立つことが分かります。
また、$\chi^2$分布は定義から再生性を持つことが分かりますが、ガンマ分布の特殊な場合であるということからもつながりを感じることができます。ちなみに$\chi^2$分布の密度関数は初見で見る気が失せる形をしていますが、ガンマ分布と親睦を深めておくと、$\chi^2$分布の密度関数にも親しみが持てるようになります(個人の意見です)。
無記憶性を持つ分布
離散分布では幾何分布、連続分布では指数分布が無記憶性を持ちます。上で述べてきた対応がさらに強固になりますね。
ここまでの内容だけでも、幾何分布・負の二項分布と指数分布・ガンマ分布は離散/連続で非常に良く対応していることが分かります。
また、感覚的な話ですが、離散分布である負の二項分布を$n → ∞$で変換すると$\chi^2$分布でガンマ分布からの流れと合流しており、こちらもきれいにつながっていると感じました。
二項分布の正規・ポアソン近似
1級に限らず、統計検定ではおなじみの関係です。発生確率$p$が非常に小さいか否かで分かれるところがポイントでしたね。
過去問では、$n$が大きくて二項分布での確率の計算が複雑すぎる場合に、近似計算として使われることが多いです。
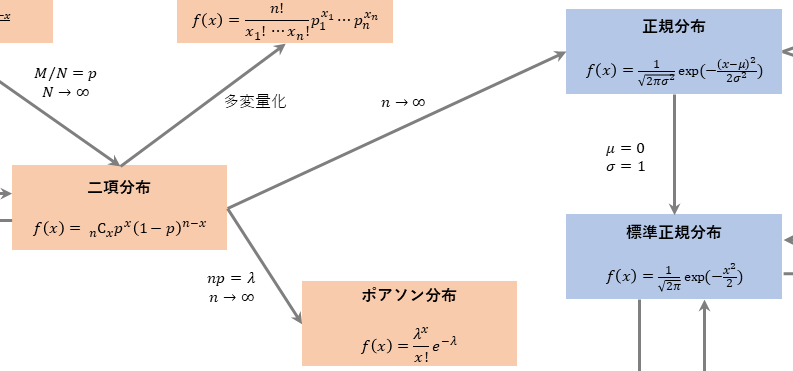
(標準)正規分布の派生形は複雑なのでがんばる
$\chi^2$分布、$T$分布、$F$分布あたりのことを指しています。
このあたりは数式が複雑で大変です。頑張って苦しみましょう。
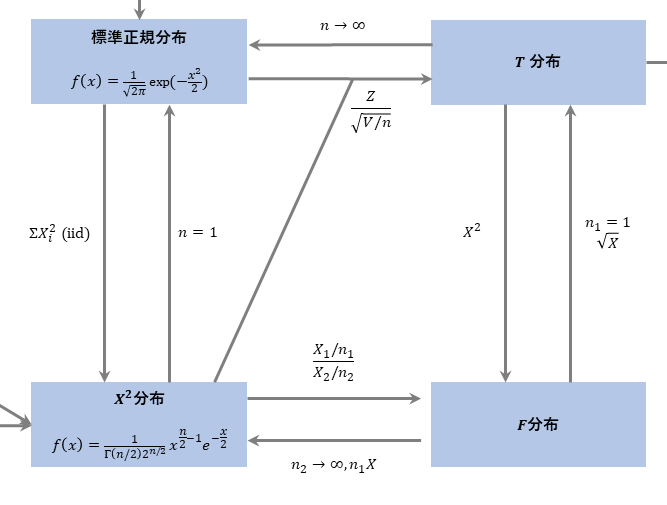
標準正規分布と$\chi^2$分布から$T$分布、$\chi^2$分布から$F$分布は定義(として扱われることが多い)なので、まずここを抑えると良いかなと思います。(参考書などで勉強をすすめると必然的にそうなると思います)
$F$分布と$T$分布は検定で用いることの方が多いため、分布同士の関係性は馴染みが薄めだと思いますが、どちらも定義に$\chi^2$分布が含まれているため、この点に着目すると$F$分布と$T$分布の対応関係も式の形から納得できるものになっています。例えば$T$分布の確率変数を二乗すると(z^2/1)/(V/n)となるため、分子に自由度1、分母に自由度$n$の$\chi^2$分布が現れ、それぞれ自由度で割られているためF分布になる、といった具合です。
ちなみに、$T$分布に従う統計量を平方根をとり変換して$F$分布の分布表を使うという知識が必要な過去問があるため、この関係も抑えておく必要があります。(大変)
枝葉の分布・関係は題材と一緒に
ここまでで、概ね図の中心部分(つながりが多い部分)の関係は整理でき、あとは丁寧にそれぞれの関係性を抑えていきます。
例えば、
- 超幾何分布と二項分布は非復元抽出と復元抽出の関係
- 指数分布とワイブル分布は生存時間解析で扱われる
のように、分布同士の関係にのテーマがあることも多いため、そのあたりを意識するとより有機的に整理することができます。そのまま大問のテーマとして問われることもあるため、過去問も進めつつ整理すると良いと思います。
おわりに
上述の通り完成系もあるためn番煎じな内容だとは思いつつ、整理の仕方に意外と個人差がではないかと思い、本記事を書いてみることにしました。ややまとまりに欠ける記事になってしまいましたが、お許しください。
拙い曼荼羅ですが、少しでも統計検定1級受験者の助けになれば幸いです。
様々な発見があり非常におもしろいので、ぜひ皆様もオリジナル曼荼羅を作りながら整理してみてください!