背景
R&Dにおいて、既存材料を代替する新しい材料を採用したときに特性がどのような応答を示すか調べたい場面は多いと思う。
このようなときは、実験しなければ何も始まらないので早く実験を始めるべきだが、材料開発のいつものパターンで、実施可能実験数に対して候補材料数が多すぎることがほとんどである。
実験のモチベーションとして、「候補材料 (既存材料から機械的な手法で生成した仮想分子や、試薬リストなど) の空間に対して、なるべく少ない実験数で傾向を把握したい」というものを想定したとき、似たような応答を示す候補をいくつも実験せずに、応答が異なる候補のみを効率良く選択することが望ましい。
JohnsonとMaggioraの類似性質原則 (similar property principle) に基づけば、構造が類似した候補をグループ化し、グループから代表して数点サンプリングすれば、実験数を減らすことができると考えられる。
そこで、上記のグループ化の1手法として、分子類似性の評価尺度である「タニモト距離 (係数)」を利用した分子のグループ化を紹介する。
タニモト距離 (係数) のイメージ
タニモト距離は以下のイメージで計算される。
-
1:
候補分子を部分構造に分解し、ある部分構造がある場合に対応する要素に1をない場合に0を入力する。(ここでの部分構造の作り方は様々な方法があり、一口にタニモト係数と言っても、値が一意に決まるわけではない点に注意)
例えば下表の場合、候補1, 2には部分構造Aがあるが、候補3には部分構造Aがないことを表す。
このような分子の記述方法をFinger printという。表1
候補材料 部分構造A 部分構造B 部分構造C … 候補1 1 0 1 … 候補2 1 1 1 … 候補3 0 1 0 … -
2:
2つの分子A, B間の類似度を考えるとき、共通した部分構造が多いほどその2つの分子構造は類似する。
この関係性をタニモト係数では、以下のような式で表す。
タニモト係数は類似度の指標であり、$0 \leq \rm{Tanimoto\ similarity} \leq 1$をとるので、タニモト距離としたいときは1からタニモト係数を引けばよい。$$\rm{Tanimoto\ similarity} = \frac{c}{a+b-c}$$
- a : 分子Aの1の数
- b : 分子Bの1の数
- c : 分子A, Bで共通した部分構造に1がある数
タニモト距離を使って候補分子間の全ての距離を計算すれば距離行列が得られるので、階層クラスタリングに持ち込むことができるようになる。
実装
ライブラリのインポート
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
import ptitprince as pt
import japanize_matplotlib
from scipy.spatial.distance import squareform
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
from rdkit import Chem
from rdkit.DataStructs import BulkTanimotoSimilarity
from rdkit.Chem import Descriptors, AllChem, DataStructs
from rdkit.ML.Descriptors import MoleculeDescriptors
from rdkit.Chem import PandasTools, Draw
関数の定義
一般的なFinger printの1つである、ECFPを計算する関数を定義する。
一見複雑だが、こちらの特徴量生成ブロックの枠組みに従って実装した。
私はこの枠組みを採用してから仕事がとても楽になったので、皆様にも特徴量生成の枠組みで試してみてほしい。
class AbstractBaseBlock:
def fit(self, input_df: pd.DataFrame, y=None):
return self.transform(input_df)
def transform(self, input_df: pd.DataFrame) -> pd.DataFrame:
raise NotImplementedError()
class MorganFingerprintBlock(AbstractBaseBlock):
def __init__(
self,
whole_df: pd.DataFrame,
column: str,
radius: int=2,
):
"""
Morgan Fingerprintを計算
Parameters
----------
whole_df : pd.DataFrame
全ての化合物のデータフレーム
column : str
対象列
radius : int, optional
Morgan Fingerprintの半径, by default 2
"""
self.whole_df = whole_df
self.column = column
self.radius = radius
self.whole_cano_smiles = [Chem.MolToSmiles(Chem.MolFromSmiles(s)) for s in whole_df[column]]
self.whole_mols = [Chem.MolFromSmiles(s) for s in self.whole_cano_smiles]
def fit(self, input_df: pd.DataFrame):
"""
Parameters
----------
input_df : pd.DataFrame
Training data
Returns
-------
pd.DataFrame
"""
num_bit = 2048
bit_arr = []
self.whole_fingerprint = []
self.whole_bitinfo = []
for mol in self.whole_mols:
bi = {}
fp_arr = np.zeros(num_bit, dtype=int)
fp = AllChem.GetMorganFingerprintAsBitVect(mol, self.radius, num_bit, bitInfo=bi)
DataStructs.ConvertToNumpyArray(fp, fp_arr)
bit_arr.append(fp_arr)
self.whole_fingerprint.append(fp)
self.whole_bitinfo.append(bi)
bit_arr = np.array(bit_arr)
self.whole_bit_df = pd.DataFrame(
bit_arr,
index=self.whole_df.index
)
out_df = self.transform(input_df)
return out_df
def transform(self, input_df: pd.DataFrame):
"""
Parameters
----------
input_df : pd.DataFrame
Test data
Returns
-------
pd.DataFrame
"""
out_df = self.whole_bit_df.loc[input_df.index, :]
return out_df.add_prefix(f'{self.column}_FPbit_')
データの読込み
いつも通り、明治大学 金子研究室HPのlogSのデータセットを使用する。
どうやらこのデータセットには重複があるようなので、一応処理しておく。
def load_smi():
import_df = pd.read_csv(
'http://datachemeng.wp.xdomain.jp/wp-content/uploads/2017/04/logSdataset1290.smi',
delimiter='\t', index_col=0, header=None
)
import_df = import_df.dropna(axis=0, how='all').dropna(axis=1, how='all')
import_df.columns = ['SMILES']
cano_smiles = [Chem.MolToSmiles(Chem.MolFromSmiles(s)) for s in import_df['SMILES']]
import_df.index = cano_smiles
import_df['SMILES'] = cano_smiles
return import_df
smiles_df = load_smi()
smiles_df.columns = ['SMILES']
print('Duplicate records:', smiles_df[smiles_df.duplicated()])
smiles_df = smiles_df.drop_duplicates()
smiles_df
finger printの計算
ECFP4を計算する。
ECFP4の概要は、ある原子に着目し、その周囲2つ先の原子までを部分構造として定義する方法である。
fp_generator = MorganFingerprintBlock(smiles_df, 'SMILES')
fp_df = fp_generator.fit(smiles_df)
このfp_dfに表1の情報が入っている。
タニモト距離の計算
tanimoto_arr = np.array(
[
BulkTanimotoSimilarity(v, fp_generator.whole_fingerprint, returnDistance=True)
for v in fp_generator.whole_fingerprint
]
)
階層クラスタリングの実行
以下のコードで階層クラスタリングを実行。
タニモト距離の配列を squareform() に渡しているが、こうしなければ距離行列として linkage() に認識されず、データとしてクラスタリングが実行されてしまう。
外部で距離行列を用意した場合、必ず squareform() で配列を変形してから、クラスタリングを実行すること。
res_clust = linkage(squareform(tanimoto_arr), method='ward')
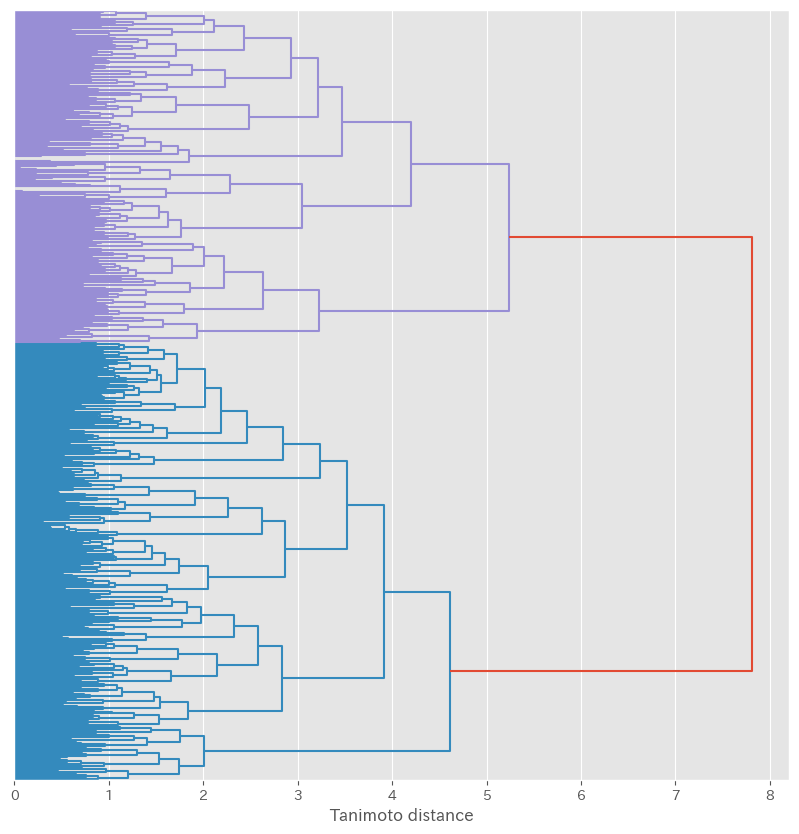
クラスタリングの結果をデンドログラムで確認する。
今回は数が多すぎて軸ラベルに分子名を表示すると大変なことになるので、デンドログラム中から省略。
dendrogram(res_clust, orientation='right')
plt.xlabel('Tanimoto distance')
plt.tick_params(labelleft=False)
plt.grid(axis='y')
plt.show()
距離2.5以内のサンプルをクラスターとして、labelを付与する。
距離の閾値は人の恣意性が入るが、ここはどうしようもない部分。(今回は実装の紹介のため本当にてきとう。実務では専門知識を持つ人に確認を取りながら設定すること。)
一応、距離やクラスタ数を計算で決定する方法もあるが、往々にして人が決定した方が早くて結果も妥当なことが多い印象。
何でもかんでも機械学習で恣意性をなくして自動化する方向に持っていこうとする人が多いが、時間がかかったり結果に劇的な差がなかったりなど、本来達成したい目的に対して貢献しないことも多い。
clust_df = pd.Series(
fcluster(res_clust, thr, criterion='distance'),
index=smiles_df.index,
name='label'
).astype('category')
各グループの分子を確認
for label in np.unique(clust_df):
print('★' * 20, label, '★' * 20)
g = Draw.MolsToGridImage(
[
Chem.MolFromSmiles(s) for s in
pd.concat(
[clust_df, smiles_df],
axis=1
).query('label == @label')['SMILES']
],
molsPerRow=10,
subImgSize=(200, 200),
maxMols=1000,
legends=(
pd.concat([clust_df, smiles_df], axis=1)
.query('label == @label')['SMILES']
.to_list()
)
)
display(g)
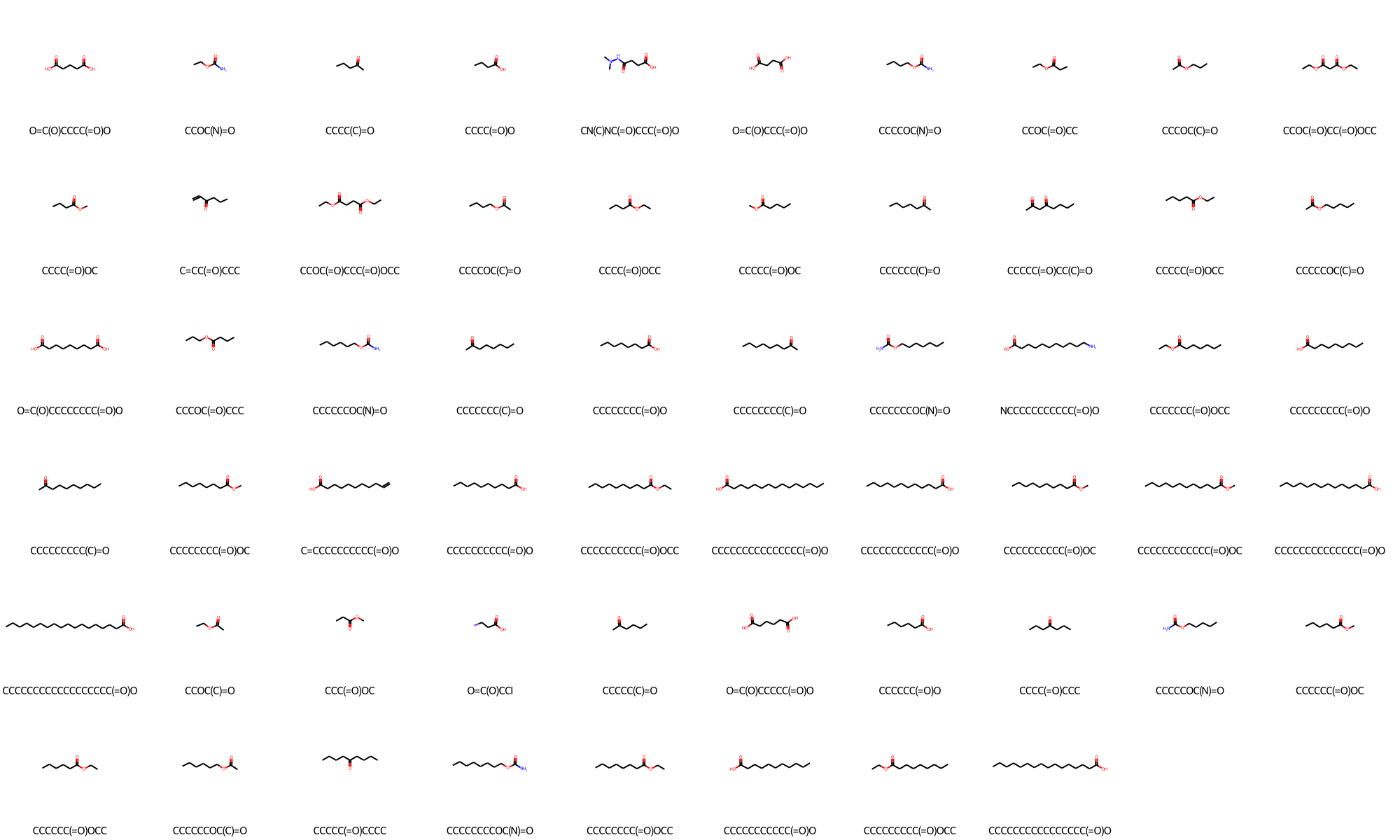
上を実行すると全てのグループを確認できるが、ここでは例として、グループ1と15を確認してみる。
グループ1では -Cl が付いた分子が、グループ15では直鎖状でカルボニル基が付いた分子が属している様子が見られる。
最後に
これで階層クラスタリングを利用した分子のグループ化ができるようになった。
各グループから任意の数ずつ分子をピックアップすれば、少ない実験回数で候補材料内を効率よく探索する実験条件となることが期待できる。
各グループに属する分子の数に差があるのであれば、比例配分法などでピックアップする数を調整すればよい。
他にも分子をグループ化する方法はいくつもあるので、どの分子から実験しようか迷ったときには、周りの統計・データサイエンスに詳しい人に相談してみてほしい。