【ラビットチャレンジ】 機械学習 第2章 非線形回帰モデル

非線形回帰モデル

• 複雑な非線形構造を内在する現象に対して，非線形回帰モデリングを実施．
• 回帰関数として，基底関数($\phi$)と呼ばれる既知の非線形関数とパラメータベクトルの線形結合を考える．
  → 未知パラメータを線形回帰モデルと同様に最小二乗法や最尤法により推定できる．$$y_i=w_0+\sum_{i=1}^mw_j\phi_j(\boldsymbol{x})+\epsilon_i$$
• よく使われる基底関数
  • 多項式関数
  • ガウス型基底関数
  • スプライン関数/Bスプライン関数

基底展開法

線形回帰と同じ枠組みで推定可能
-説明変数$$\boldsymbol{x}_i=(x_{i1},x_{i1},\cdots,x_{im})\in\mathbb{R}^m$$

-非線形関数ベクトル$$\boldsymbol{\phi}(\boldsymbol{x}_i) = (\phi_1(\boldsymbol{x}_i),\phi_2(\boldsymbol{x}_i),\cdots,\phi_k(\boldsymbol{x}_i))^T\in\mathbb{R}^k$$
-非線形関数の計画行列$$\Phi^{(train)}=(\boldsymbol{\phi}(\boldsymbol{x}_1),\boldsymbol{\phi}(\boldsymbol{x}_2),\cdots,\boldsymbol{\phi}(\boldsymbol{x}_n))^T\in\mathbb{R}^{n\times k}$$
-最尤法による予測値$$\hat{\boldsymbol{y}}=\Phi(\Phi^{(train)T}\Phi^{(train)})^{-1}\Phi^{(train)T}\boldsymbol{y}^{(train)}$$

正則化法

• モデルの複雑さ

  • チューニングパラメータ（基底関数の数やバンド幅）によりモデルの複雑さが変化
  • 適切な複雑さを持つモデルを適用しないと過学習や未学習の問題が発生
  • 未学習：学習データに対して十分小さな誤差が得られないモデル
  • 過学習：小さな誤差は得られたが，テスト集合誤差との差が大きいモデル

• モデルの複雑さに伴って，その値が大きくなる正則化項（罰則項）$R$ を課した関数の最小化を行う．

• 正則化項（罰則項）$R$

  • 形状によっていくつもの種類があり，それぞれ推定量の性質が異なる
  • 正則化項なし → 最小２乗推定
  • L2ノルムを利用 → Ridge推定量 縮小推定
  • L1ノルムを利用 → Lasso推定量 スパース推定

• 正則化（平滑化）パラメータ $\gamma\hspace{6pt} (>0)$

  • モデルの曲線の滑らかさを調節する．→適切に決める必要あり． $$S_{\gamma}=(\boldsymbol{y}-\boldsymbol{\Phi w})^T(\boldsymbol{y}-\boldsymbol{\Phi w})+\gamma R(\boldsymbol{w})$$

モデルの汎化性能測定

汎化性能

• 学習に使用した入力ではなく，新たな入力に対する予測性能
  • （学習誤差ではなく）汎化性能（テスト誤差）が小さいものが良い性能を持ったモデル．

モデルの評価

• ホールドアウト法

  • 有限のデータを学習用とテスト用の２つに分割する．
  • 学習用データとテスト用データの比率の調整が難しい．
  • つまり，手元にデータが大量にある場合を除いて，良い性能評価を得られない．

• クロスバリデーション法（交差検証）

  • データを$N$個に分割し，その一つを検証データ，残りを学習データとして各モデルの精度を$N$回計測する．
  • その精度の平均をCV（クロスバリデーション）値と呼ぶ．

ハンズオン

skl_nonlinear_regression.ipynb

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns #matplotlibのラッパー

%matplotlib inline

skl_nonlinear_regression.ipynb

#seaborn設定
sns.set() #設定をクリアしてデフォルトに
#背景変更
sns.set_style("darkgrid", {'grid.linestyle': '--'})
#大きさ(スケール変更)
sns.set_context("paper")

skl_nonlinear_regression.ipynb

n=100

def true_func(x):
 z = 1-48*x+218*x**2-315*x**3+145*x**4
 return z

def linear_func(x):
 z = x
 return z

skl_nonlinear_regression.ipynb

# 真の関数からノイズを伴うデータを生成

# 真の関数からデータ生成
data = np.random.rand(n).astype(np.float32) # random.rand(n): 0-1の乱数をn作る．
data = np.sort(data)
target = true_func(data)

# 　ノイズを加える
noise = 0.5 * np.random.randn(n) # random.randn(n): 平均0, 標準偏差1の正規分布．つまり，-１~1の値を出力．
target = target + noise

# ノイズ付きデータを描画

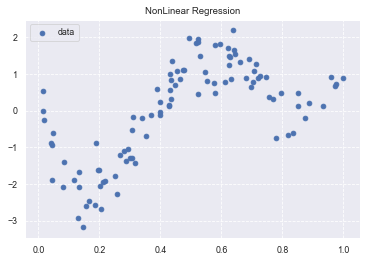
plt.scatter(data, target, label='data')

plt.title('NonLinear Regression')
plt.legend(loc=2)

skl_nonlinear_regression.ipynb

# 線形回帰を行う
from sklearn.linear_model import LinearRegression

clf = LinearRegression()
data = data.reshape(-1,1) # 次元0に-1を指定すると，縦ベクトルとなる．
target = target.reshape(-1,1) # 次元0に-1を指定すると，縦ベクトルとなる．
clf.fit(data, target)

p_lin = clf.predict(data)

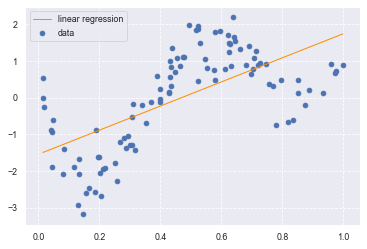
plt.scatter(data, target, label='data')
plt.plot(data, p_lin, color='darkorange', marker='', linestyle='-', linewidth=1, markersize=6, label='linear regression')
plt.legend()
print(clf.score(data, target)) # 決定係数を出力

0.41320782764293906

skl_nonlinear_regression.ipynb

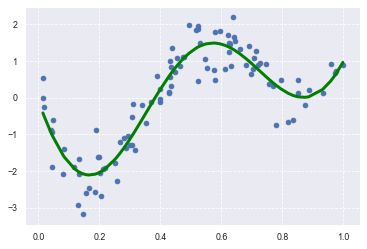
# KernelRidgeによるガウスカーネルモデル．L2制約付き最小二乗学習
from sklearn.kernel_ridge import KernelRidge

clf = KernelRidge(alpha=0.0002, kernel='rbf')
# Parameters
# alpha : ペナルティの大きさ
# kernel : RBFカーネル(Radial basis function kernel)

clf.fit(data, target)

p_kridge = clf.predict(data)

# グラフ出力
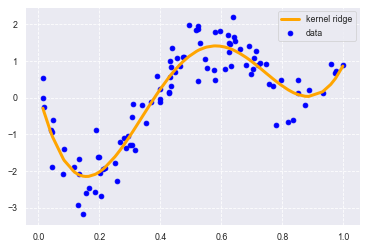
plt.scatter(data, target, color='blue', label='data')

plt.plot(data, p_kridge, color='orange', linestyle='-', linewidth=3, markersize=6, label='kernel ridge')
plt.legend() # 凡例
#plt.plot(data, p, color='orange', marker='o', linestyle='-', linewidth=1, markersize=6)

print(clf.score(data, target))

0.8810414281073834

skl_nonlinear_regression.ipynb

#Ridge

from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Ridge

kx = rbf_kernel(X=data, Y=data, gamma=50) # 放射基底関数カーネルを計算する
#KX = rbf_kernel(X, x)

#clf = LinearRegression()
clf = Ridge(alpha=30)
clf.fit(kx, target)

p_ridge = clf.predict(kx)

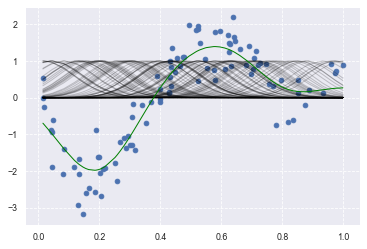
plt.scatter(data, target,label='data')
for i in range(len(kx)):
 plt.plot(data, kx[i], color='black', linestyle='-', linewidth=1, markersize=3, label='rbf', alpha=0.2)

#plt.plot(data, p, color='green', marker='o', linestyle='-', linewidth=0.1, markersize=3)
plt.plot(data, p_ridge, color='green', linestyle='-', linewidth=1, markersize=3,label='ridge regression')
#plt.legend()

print(clf.score(kx, target))

0.8584537190867131

skl_nonlinear_regression.ipynb

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline

skl_nonlinear_regression.ipynb

#PolynomialFeatures(degree=1)

plt.scatter(data, target)
# 多項式基底を作成する．

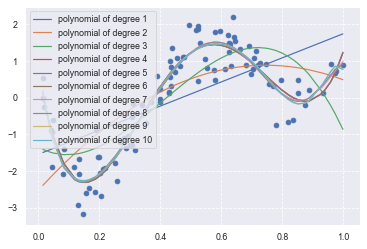
deg = [1,2,3,4,5,6,7,8,9,10]
for d in deg:
 regr = Pipeline([
 ('poly', PolynomialFeatures(degree=d)),
 ('linear', LinearRegression())
 ])
 regr.fit(data, target)
 # make predictions
 p_poly = regr.predict(data)
 # plot regression result
 plt.plot(data, p_poly, label='polynomial of degree %d' % (d))
 plt.legend(loc=2)
 print('{0:02d} {1:.15f}'.format(d, regr.score(data, target)))

01 0.413207829272240
02 0.518749151434800
03 0.628357884957680
04 0.887010123781958
05 0.887044166055853
06 0.887053035036568
07 0.889536170289383
08 0.889801333789919
09 0.890876035316865
10 0.890760870143186

skl_nonlinear_regression.ipynb

#Lasso

from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Lasso

kx = rbf_kernel(X=data, Y=data, gamma=5)
#KX = rbf_kernel(X, x)

# alphaを減らしてiterを増やした
lasso_clf = Lasso(alpha=0.001, max_iter=100000)
lasso_clf.fit(kx, target)

p_lasso = lasso_clf.predict(kx)

plt.scatter(data, target)

#plt.plot(data, p, color='green', marker='o', linestyle='-', linewidth=0.1, markersize=3)
plt.plot(data, p_lasso, color='green', linestyle='-', linewidth=3, markersize=3)

print(lasso_clf.score(kx, target))

0.8798552752769152

skl_nonlinear_regression.ipynb

#from sklearn import cross_validation, preprocessing, linear_model, svm
from sklearn import model_selection, preprocessing, linear_model, svm
# model_selectionに変更．

# SVR-rbf
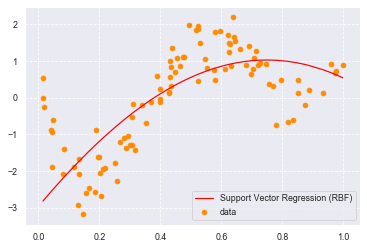
clf_svr = svm.SVR(kernel='rbf', C=1e3, gamma=0.1, epsilon=0.1)
target1=np.reshape(target,(-1))
clf_svr.fit(data, target1)
y_rbf = clf_svr.predict(data)

# plot
plt.scatter(data, target, color='darkorange', label='data')
plt.plot(data, y_rbf, color='red', label='Support Vector Regression (RBF)')
plt.legend()
plt.show()

skl_nonlinear_regression.ipynb

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.1, random_state=0)

skl_nonlinear_regression.ipynb

from keras.callbacks import EarlyStopping, TensorBoard, ModelCheckpoint

# cb_cp = ModelCheckpoint('./out/checkpoints/weights.{epoch:02d}-{val_loss:.2f}.hdf5', verbose=1, save_weights_only=True)
cb_cp = ModelCheckpoint('./weights.{epoch:02d}-{val_loss:.2f}.hdf5', verbose=1, save_weights_only=True) # ディレクトリの変更

cb_tf = TensorBoard(log_dir='./out/tensorBoard', histogram_freq=0)

Using TensorFlow backend.

skl_nonlinear_regression.ipynb

from keras.models import Sequential
from keras.layers import Input, Dense, Dropout, BatchNormalization
from keras.wrappers.scikit_learn import KerasRegressor

# 隠れ層の活性化関数をRelu，出力層の活性化関数をSigmoidとしてSequentialモデルを構築する
def relu_model():
 model = Sequential()
 model.add(Dense(10, input_dim=1, activation='relu'))
 model.add(Dense(8, activation='relu'))
 model.add(Dense(5, activation='relu'))
 model.add(Dense(3, activation='sigmoid'))
 model.add(Dense(1))

 model.compile(loss='mean_squared_error', optimizer='adam')
 return model

# use data split and fit to run the model
estimator = KerasRegressor(build_fn=relu_reg_model, epochs=100, batch_size=5, verbose=1)

history = estimator.fit(x_train, y_train, callbacks=[cb_cp, cb_tf], validation_data=(x_test, y_test))

Train on 90 samples, validate on 10 samples
Epoch 1/100
90/90 [==============================] - 6s 71ms/step - loss: 1.4577 - val_loss: 6.3816

Epoch 00001: saving model to ./weights.01-6.38.hdf5
Epoch 2/100
90/90 [==============================] - 4s 42ms/step - loss: 1.6469 - val_loss: 1.5418

Epoch 00002: saving model to ./weights.02-1.54.hdf5
Epoch 3/100
90/90 [==============================] - 4s 42ms/step - loss: 0.8780 - val_loss: 1.3294

Epoch 00003: saving model to ./weights.03-1.33.hdf5
Epoch 4/100
90/90 [==============================] - 4s 49ms/step - loss: 0.9645 - val_loss: 1.0802

Epoch 00004: saving model to ./weights.04-1.08.hdf5
Epoch 5/100
90/90 [==============================] - 5s 55ms/step - loss: 0.5584 - val_loss: 1.0554

Epoch 00005: saving model to ./weights.05-1.06.hdf5
Epoch 6/100
90/90 [==============================] - 4s 49ms/step - loss: 0.6439 - val_loss: 0.8581

Epoch 00006: saving model to ./weights.06-0.86.hdf5
Epoch 7/100
90/90 [==============================] - 4s 47ms/step - loss: 0.5219 - val_loss: 0.8335

Epoch 00007: saving model to ./weights.07-0.83.hdf5
Epoch 8/100
90/90 [==============================] - 4s 46ms/step - loss: 0.5783 - val_loss: 0.7498

Epoch 00008: saving model to ./weights.08-0.75.hdf5
Epoch 9/100
90/90 [==============================] - 5s 55ms/step - loss: 1.2041 - val_loss: 2.0974

Epoch 00009: saving model to ./weights.09-2.10.hdf5
Epoch 10/100
90/90 [==============================] - 5s 52ms/step - loss: 1.4860 - val_loss: 0.9596

Epoch 00010: saving model to ./weights.10-0.96.hdf5
Epoch 11/100
90/90 [==============================] - 4s 49ms/step - loss: 0.7680 - val_loss: 0.9596

~~ 中略 ~~
Epoch 00096: saving model to ./weights.96-0.41.hdf5
Epoch 97/100
90/90 [==============================] - 4s 45ms/step - loss: 0.3910 - val_loss: 0.3375

Epoch 00097: saving model to ./weights.97-0.34.hdf5
Epoch 98/100
90/90 [==============================] - 4s 47ms/step - loss: 0.3179 - val_loss: 0.4850

Epoch 00098: saving model to ./weights.98-0.48.hdf5
Epoch 99/100
90/90 [==============================] - 5s 52ms/step - loss: 0.2999 - val_loss: 0.1813

Epoch 00099: saving model to ./weights.99-0.18.hdf5
Epoch 100/100
90/90 [==============================] - 4s 48ms/step - loss: 0.3322 - val_loss: 0.2278

Epoch 00100: saving model to ./weights.100-0.23.hdf5

skl_nonlinear_regression.ipynb

y_pred = estimator.predict(x_train)

90/90 [==============================] - 0s 4ms/step

skl_nonlinear_regression.ipynb

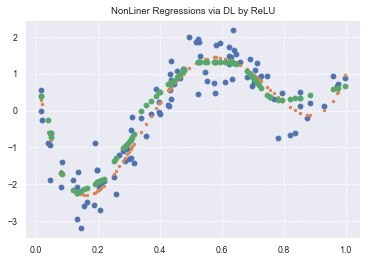
plt.title('NonLiner Regressions via DL by ReLU')
plt.plot(data, target, 'o')
plt.plot(data, true_func(data), '.')
plt.plot(x_train, y_pred, "o", label='predicted: deep learning')
#plt.legend(loc=2)

skl_nonlinear_regression.ipynb

print(lasso_clf.coef_)

[ -0. -0. -0. -0. -0. -0.
-0. -0. -0. -7.960358 -5.6067443 -0.5237518
-0.4339014 -2.9543405 -0.9058812 -0. -0. -0.
-0. -0. -0. -0. -0. -0.
-0. -0. -0. -0. -0. -0.
-0. -0. -0. -0. -0. -0.
-0. -0. -0. -0. -0. -0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
-0. -0. -0. -0. -0. -0.
-0. -0. -0. -0. -0. -0.
-0. -0. -0. -0. -0. -0.
-0. -0. -0. -0. -0. -0.
-0. -0. -0. -0. -2.4459205 -13.672384
-0. -0. -0. -0. ]

DeepLearning ラビットチャレンジ