概要
3Dのアクションゲームに物理演算は欠かせない存在です。
Unityでは標準で物理エンジンが搭載されているので、ただ平面や立体を並べてRigidbodyをくっつけて再生するだけで、物理法則に従った楽しい動きをしてくれます。
ただ、それを知りつつ物理演算は自前で実装されている方も多いのではないでしょうか?
実際にゲームを作っていると、爽快感を増すためにウソの物理法則を時々差し込みたかったりすることもあります。
さらに、物理エンジンに頼っていると, 物体がブルブル震えてしまったり コライダを突き破ったりという問題に頭を悩ませることもあります。
そこまでリアルな動きを求めているわけではない場合は、シンプルな物理モデルを自前で実装するほうが簡単で良い場合もあります。
たとえば僕のゲームでは, 物理演算は以下のような単純な運動方程式のモデルで統一しています。
\begin{equation}
m\vec{a} = m\vec{g} - k\vec{v} \\
\end{equation}
$\vec{g}=$重力加速度ベクトル
$\vec{a}=$物体の加速度ベクトル
$\vec{v}=$物体の速度ベクトル
基本的には物体にかかる力は重力と速度に一次比例する空気抵抗のみということですね。
今回はこの物理法則のなかで、物体を射出した際の特定の着弾点に到達するために必要な初速度を求めようと思います。
準備
まずは動作を確認するためにクリックした位置に着弾するようにボールを射出するサンプルを作りました。
まだ射出速度をいくらにすればいいのかはわからないので, 射出速度は定数にしてあります。
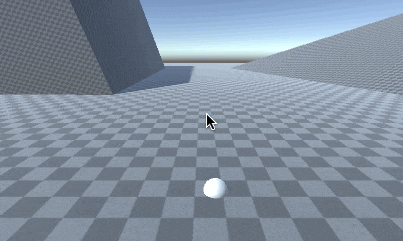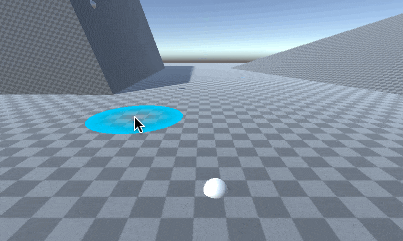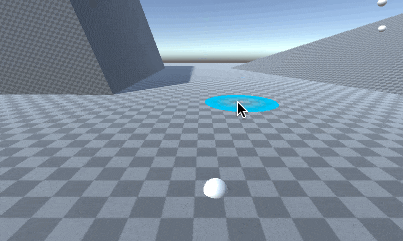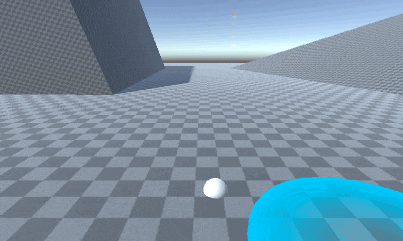
方向は合ってますが、到達距離が全然あってませんね。
射出速度を調整すれば、クリックしたところにちょうど到達してくれるはずです!

ちなみに、横から見ると空気抵抗によって放物線がゆがんでいるのが確認できます。
空気抵抗のないきれいな放物線なら射出速度は簡単に求まるのですが..
数式を解く
出発の式はさきほどの運動方程式です。
\begin{equation}
m\vec{a} = m\vec{g} - k\vec{v} \\
\end{equation}
速度ベクトルと加速度ベクトルはそれぞれ位置ベクトルの一回微分、二回微分であることに注意しながら、x方向とy方向それぞれに関する2つの式に分離します。
\begin{eqnarray}
\left\{
\begin{array}{l}
m\frac{d^2x}{dt^2} + k\frac{dx}{dt} = 0 \\
m\frac{d^2y}{dt^2} + k\frac{dy}{dt} + mg = 0
\end{array}
\right.
\end{eqnarray}
重力はy方向にのみかかりますので、重力加速度gはyの式にだけ登場します。
この二階微分方程式を解いて、座標の式に直します。
ラプラス変換を用いて計算すると比較的簡単に求めることができます。
※wikipediaとこちらを参考にさせていただきました。
するとこのようになります。
\begin{eqnarray}
\left\{
\begin{array}{l}
x = \frac{m}{k}v_0(1-e^{-\frac{k}{m}t})cos\theta \\
y = \frac{m}{k}\{(v_0sin\theta + \frac{m}{k}g)(1-e^{-\frac{k}{m}t}) - gt\} + y_0
\end{array}
\right.
\end{eqnarray}
さて、ここから射出時の速度$v_0$を求めていきます。
時刻$T$において$x=L$の地点に着弾するとするということで、$x=L,t=T,y=0$を代入してひとまず下の式が得られます。
変数は$v_0$と$T$ということになります。
\begin{eqnarray}
\left\{
\begin{array}{l}
L = \frac{m}{k}v_0(1-e^{-\frac{k}{m}T})cos\theta \\
0 = \frac{m}{k}\{(v_0sin\theta + \frac{m}{k}g)(1-e^{-\frac{k}{m}T}) - gT\} + y_0
\end{array}
\right.
\end{eqnarray}
変数をひとつ消したいので、上の式を$v_0$について解きます。
\begin{equation}
v_0 = \frac{k}{m}\frac{L}{(1-e^{-\frac{k}{m}T})cos\theta}
\end{equation}
となり、下の式に代入して整理すると
\begin{equation}
-\frac{m}{k}g{\cdot}e^{-\frac{k}{m}T}-gT+tan\theta\frac{k}{m}L + \frac{m}{k}g + \frac{k}{m}y_0 = 0
\end{equation}
が得られます。
これでは少しぐちゃぐちゃで式の本質が見えずらいので一旦定数をまとめます。
\begin{eqnarray}
\left\{
\begin{array}{l}
ae^{bT} + cT + d = 0 \\
a = -\frac{m}{k}g \\
b = -\frac{k}{m} \\
c = -g \\
d = tan\theta\frac{k}{m}L + \frac{m}{k}g + \frac{k}{m}y_0 \\
\end{array}
\right.
\end{eqnarray}
さて、この方程式を$T=$のかたちに直せることができれば勝ちなのですが
残念ながら$log$や$sin$などの初等関数でT=の形に表現することはできません。
(指数関数の近似式「$e^x\sim 1+ax+\frac{a^2}{2}x^2$」を使用すると二次方程式に持ち込めますが, それだと精度が悪かったです...)
どうしようかと悩んでいたところ、このサイトにズバリどうすればよいかが記されていました。
Using Lambert W function, x=aexx=aex can be rewritten as (−x)e−x=−a(−x)e−x=−a, hence x=−W(−a)x=−W(−a).
Note that this is not much more than a rewriting of the equation, hence the fact that Lambert W function was given a definition and that xx can be expressed through it does not lead us closer to a "solution", if you ask me.
なるほど..
つまり普通の関数ではT=の形に表現できないけど,「ランベルトのW関数」を導入すれば表現できるよ!ってことですね.
ランベルトのW関数というのは、以下の関数の逆関数のことらしいです。
\begin{equation}
F(x)=xe^x
\end{equation}
※ランベルトのW関数は$F(x)$ではなく$F^{-1}(x)$です。
では早速このサイトを参考にしながら、先ほどの式を変形していきます。
\begin{equation}
ae^{bT} + cT + d = 0 \\
\end{equation}
まずは$y=cT+d$として変数を置き換えます。
\begin{equation}
ae^{\frac{b}{c}(y-d)}+y = 0 \\
\end{equation}
うまく変形してランベルトのW関数が使える形に持っていきます。
\begin{equation}
ae^{\frac{b}{c}y}{\cdot}e^{-\frac{bd}{c}}+y = 0 \\
a{\cdot}e^{-\frac{bd}{c}}+y{\cdot}e^{-\frac{b}{c}y} = 0 \\
-\frac{b}{c}y{\cdot}e^{-\frac{b}{c}y} = \frac{ab}{c}{\cdot}e^{-\frac{bd}{c}} \\
\end{equation}
ランベルトのW関数:$W(x)$を使って、$y$について解きます。
\begin{equation}
-\frac{b}{c}y = W(\frac{ab}{c}{\cdot}e^{-\frac{bd}{c}}) \\
y = -\frac{c}{b}W(\frac{ab}{c}{\cdot}e^{-\frac{bd}{c}}) \\
\end{equation}
あとは$y$を$T$に戻して整理するだけで, $T$について解けます。
\begin{equation}
T = -\frac{d}{c} -\frac{1}{b}W(\frac{ab}{c}{\cdot}e^{-\frac{bd}{c}})
\end{equation}
もう代入はしませんが, $T$について解けたということは$v_0$についても解けますね!
実装する
基本的には上記の数式を計算するだけですが、
ランベルトのW関数だけは標準的な関数ではないのでMathfなどにも実装されていません。
この関数は初等関数では表現できませんので, 近似解を求めて使用するしかありません。
wikipediaに漸化式を用いて近似解を求める方法が示されていましたので、そちらを利用しました。
ランベルトのW関数も含めたコード全文は以下のようになります。
public static float GetInitialVelocity (float gravity , float resistance , float mass , float distance , float theta , float offsetY){
var k = resistance;
var g = gravity;
var m = mass;
var y0 = offsetY;
var r = theta/180.0f * Mathf.PI;
var L = distance;
var A = -m/k*g;
var B = -k/m;
var C = -g;
var D = k/m * y0 + Mathf.Tan(r)*k/m*L + m/k * g;
var T = - D/C - 1.0f/B * GetLambertW(A*B/C * Mathf.Exp(-B*D/C));
return k*L/m / (1.0f-Mathf.Exp(-k/m*T)) / Mathf.Cos(r);
}
public static float GetLambertW(float x) {
var res = _Prec_LambertW( x, _Desy_LambertW(x));
return res;
}
static float _Prec_LambertW(float x, float initial = 0, float prec = 0.00000001f , int iteration = 100){
var w = initial;
var i = 0;
for (i =0 ; i< iteration ; i++){
var wTimesExpW = w * Mathf.Exp(w);
var wPlusOneTimesExpW = (w+1) * Mathf.Exp(w);
if (prec > Mathf.Abs((x-wTimesExpW) / wPlusOneTimesExpW)){
break;
}
w = w - (wTimesExpW-x)/(
wPlusOneTimesExpW - (w+2)*(wTimesExpW-x)/(2*w+2));
}
return w;
}
static float _Desy_LambertW(float x) {
float lx1;
if (x <= 500.0) {
lx1 = Mathf.Log(x + 1.0f);
return 0.665f * (1.0f + 0.0195f * lx1) * lx1 + 0.04f;
}
var res = Mathf.Log(x - 4.0f) - (1.0f - 1.0f/Mathf.Log(x)) * Mathf.Log(Mathf.Log(x));
return res;
}
結果

お〜できました!
たしかにクリックしたポイントに到達していますね!
あとがき
ここまで淡々と書きましたが、実装できるまで非常に時間がかかりました。。
実は前からこの手の問題を解決したいと思ったことはあったのですが、
微分方程式が絡むと解けないのではないかと思って、避けて通ってきました。
今回の微分方程式は比較的簡単なものではあるのですが、こうしてプログラムに実装することができたので
これから少しは実装できるプログラムの幅が広がったかなと思いました。