オイラー法による変数係数二階線形斉次微分方程式の数値計算

はじめに

$$\frac{d^2v}{dt^2}+\frac{P}{EI(t)}v=0$$
を解く.$P,E$は適当な変数で$I(t)$は今回$t$が1.0ずつ増えるにしたがって$I(t)$も1.0ずつ増えるステップ関数とする.

厳密解は

これは変数係数の二階線形斉次微分方程式なので一般的解法が存在しない.よって特殊解として$$v=t^m$$あるいは$$v=e^{mt}$$を式に代入して解となるように定数mが定まるかどうかを調べる.試しにMathematicaで
DSolve[v''[t] + (P0/E0)*(1/UnitStep[t])*v[t] == 0, v[t], {t, 1, 10}]

と入力する基本解が得られる.

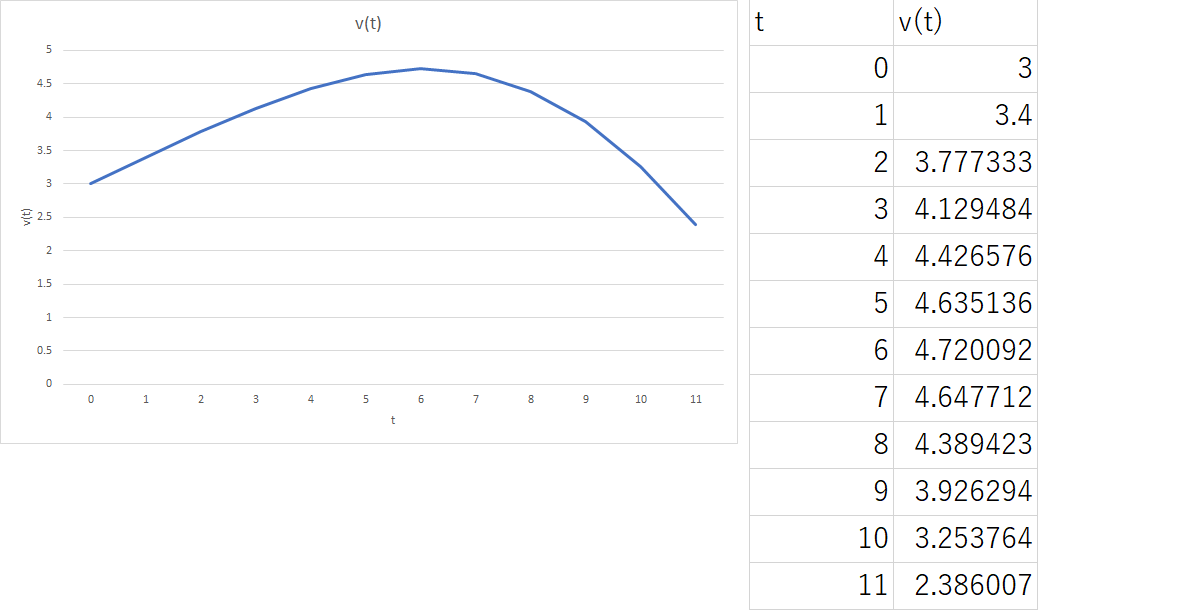
オイラー法による近似

public static void main(String[] args) {
        double v0=3.0,z0=4.0,h=0.1;//初期値
        int n=10;
        double v,z,z1;//変数
        double p= 2.0;//変数
        double e= 3.0;//変数
        double ix= 1.0;//ステップ関数I(x)の初期値
        System.out.println(v0);//vの初期値出力
        v = v0 +z0*h;//v1計算
        z = z0 - (p/e*ix)*v*h;//z1計算
        System.out.println(v);//v1出力
        for(int i=0;i<n;i++){
            v = v + z*h;//v2からv12まで計算
                z1 = z - ((p/e)*ix)*v*h;
                z = z1;
                ix++;
            System.out.println(v);//v出力
        }
    }

を実行すると以下のような結果になる.

参考文献

[1]三井田　惇郎,須田　宇宙：数値計算法[第二版],森北出版株式会社,2017
[2]稲岡　毅：基礎からの微分方程式,森北出版株式会社,2018