Juliaで微分

パッケージPlotsの追加

コマンドラインでjulia起動して以下の通り

julia> Pkg.add("Plots")

驚くほど時間かかります。

sin関数の微分

using Plots

# 入力xの範囲を決める
# piは円周率のπのこと
# -3.14から+3.14まで0.01刻み
# つまり-180°～180°
x = -pi:0.01:pi

# 関数f(x)の定義
# 今回はサイン関数
f(x) = sin(x)

# ⊿xを決める
# なるべく0に近い数字がいい
⊿x = 0.0001

# f(x)の微分関数df(x)
df(x) = (f(x+⊿x)-f(x))/⊿x

# グラフを描く
# xは配列なので関数の末尾に.をつける(各要素ごとに演算する)
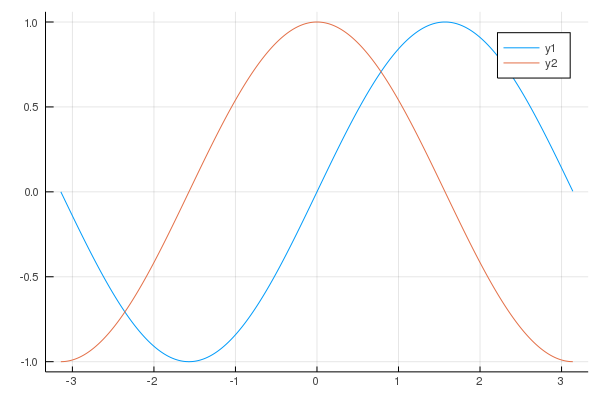
plot(x,[f.(x), df.(x)])

y1がf(x)
y2がdf(x)
sin(x)を微分するとcos(x)になるのでうまくいっていそうです。

もうすこし複雑な関数をやってみる

using Plots

# 入力x
x = -pi:0.01:pi

# 関数f(x)
f(x) = sin(x) / (cos(x) + 2)

# ⊿x
⊿x = 0.0001

# f(x)の微分関数df(x)
df(x) = (f(x+⊿x)-f(x))/⊿x

# グラフを描く
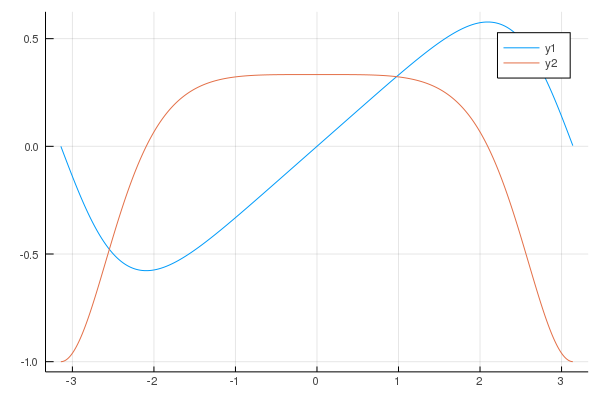
plot(x,[f.(x),df.(x)])

さっきと違うのはf(x)の定義だけ。

なんだかそれっぽい。

まとめ

プログラミング言語としての関数じゃなくて
数学的に関数書いていけるのってとても書きやすくていいですね。