勾配降下法
いろいろな呼び名
まずは言葉のいろいろな言い方として、
- 勾配降下法(こうばいこうかほう)
- GradientDiscent(グラディエントディセントン)
と呼ばれたりします。
ここでは勾配降下法と呼ぶことにします。
機械学習における勾配降下法
機械学習では、モデル(集めたデータから導き出した方程式みたいなもの)から求める予測値と集めたデータの実際の答えの差分が最小になるようにモデルを考えます。
したがって機械学習では、この差分(目的関数と呼ぶ)の最小を求めるといった手順が存在します。
この最小を求める方法のひとつが勾配降下法なのです。
勾配降下法ってどういう感じ?
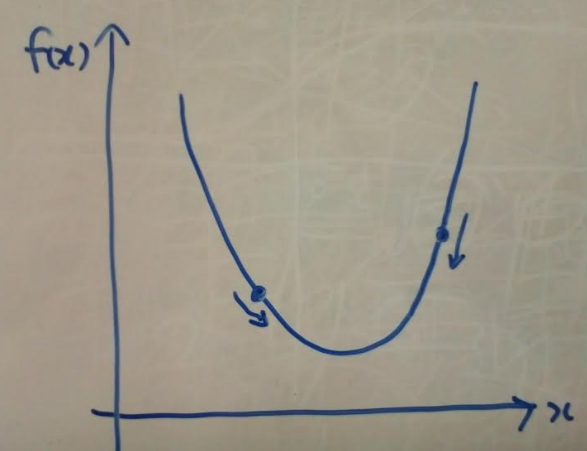
仮に目的関数を$f\left( x\right)$と仮定して、どのような方法かというと、
-
目的関数上のどこかの1点をランダムで決める。どこでもOK。 - その点の傾きが
負であれば$x$を特定量(ステップ幅と呼んだりします)分増やす、傾きが正であれば$x$を特定量分減らす。ステップ幅は自分で決めることができます。 - 増やされた、もしくは減らされた先での$x$での傾きが
負であれば$x$を特定量分増やす、傾きが正であれば$x$を特定量減らす。 - これの繰り返し(繰り返しの回数を
エポック数と呼びます) - 複数回実行した結果の$x$に対する$f\left( x\right)$が誤差関数の最小値となる。
誤差逆伝播法
いろいろな呼び名
まずは言葉のいろいろな言い方として、
- 誤差逆伝播法(ごさぎゃくでんぱほう)
- backpropagation(バックプロパゲーション)
と呼ばれたりします。
ここでは誤差逆伝播法と呼ぶことにします。
機械学習における誤差逆伝播法
勾配降下法と同様、目的関数の最小を求める方法のひとつです。
家賃を推測するモデルで、各要素として、駅からの距離、部屋数、築年数、・・・みたいな感じで、
テータ項目が非常に多い場合($x_{1},x_{2},x_{3}\ldots$のような場合)に勾配降下法よりも効果を発揮します。
具体的に勾配降下法と何が違うの?
最小を求めるポイントは微分なのですが、
$$y=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}\ldots$$
のような微分の場合、各$x_{i}$で微分しなければいけないので、計算が複雑になります。
そのような時、勾配降下法だと計算が複雑になり、計算コストが高くなってしまいます。
一方誤差逆伝播法では以下のように微分の分割の公式を利用します。
$$\dfrac {dy}{dx}=\dfrac {dy}{df}\cdot \dfrac {df}{dx}$$
何が言いたいかというと、一気に微分するのではなく、一つの要素ごとに順に微分していくというイメージです。