シグモイド関数で重要なのは難しい式ではなく、グラフの形なのです

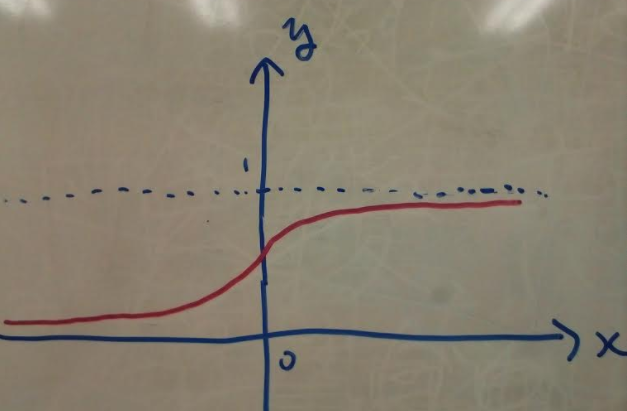
シグモイド関数の見た目

以下のような関数のことです。

シグモイド関数の数式

数式だと以下です。

$y=\dfrac {1}{1+e^{-ax}}\left( a >0\right)$

簡略化して下記のように表現されたりします。

$y=\sigma \left( x\right)$

※$\sigma$はシグマと読みます。

シグモイド関数で重要なのは難しい式ではなく、グラフの形なのです

重要なのはグラフの形です。

• x=0周辺でyがグーンと上がっている
• 滑らかな線である

上記2つの特徴があります。

機械学習の分類という領域では結果がYesかNoかを求められることがあります。
つまりx=0周辺以外は大体y=0かy=1という性質がとても使いやすいのです。

また機械学習では微分を多用します。
滑らかな線でないと微分が数学的に面倒になってしまいます。

つまり、シグモイド関数は機械学習にとって都合の良い関数なのです。