ゼロから作るDeepLearning❷の5章「RNN」をGoogle Colabで実装

※GPUの使用を想定した実装。

5章 リカレントニューラルネットワーク（RNN）

4章までで見てきたニューラルネットワークはフィードフォワードと呼ばれるタイプのネットワークだった。フィードフォワードとは流れが一方向のネットワークのことである。

フィードフォワードの問題点は、時系列データの性質（パターン）を十分に学習することができない。そこで、リカレントニューラルネットワーク（Recurrent Neural Network）、略してRNNの出番である。

フィードフォワード・ネットワークの問題点を指摘し、RNNがその問題を解決できることを説明する。また、RNNの構造を解説し、その処理をPythonで実装する。

5.1 確率と言語モデル

word2vecを確率の視点から眺める

word2vecのCBOWモデルの復習をする。

$w_1$、$w_２$、・・・、$w_r$という単語の列で表されるコーパスを考える。

t番目の単語を「ターゲット」として、その前後の単語（t-1番目とt+1番目）を「コンテキスト」として扱う。このとき、CBOWモデルが行うことは、コンテキストの$w_{t-1}$と$w_{t+1}$から、ターゲットの$w_t$を推測することである。

$w_{t-1}$と$w_{t+1}$が与えられたとき、ターゲットが$w_t$になる確率を数式に表す。

式5.1

P(w_t|w_{t-1}, w_{t+1})

CBOWモデルは、式の事後確率をモデル化する。
この事後確率は、「$w_{t-1}$と$w_{t+1}$が与えられたとき、$w_t$が起こる確率」を表す。
これがウィンドウサイズが１のときのCBOWモデルである。

今度はコンテキストとして、左側のウィンドウだけに限定してみたい。

たとえば、$w_1$、$w_２$、・・・、$w_{t-2}$、$w_{t-1}$、$w_{t}$、$w_{t+1}$、・・・$w_{T-1}$、$w_T$というコーパスがあるとき、

左側の２つの単語だけをコンテキストとして、$w_{t-2}$と$w_{t-1}$から$w_{t}$を推測する。

そうすると、CBOWモデルが出力する確率は次の式のようになる。

式5.2

$$
P(w_t|w_{t-2}, w_{t-1})
$$

式5.3は、式5.2を用いたCBOWモデルが扱う損失関数である。
損失関数は交差エントロピー誤差を用いている。

式5.3

$$
L = -logP(w_t|w_{t-2}, w_{t-1})
$$

CBOWモデルの学習で行うことは、コーパス全体の損失関数の総和をできる限り小さくする重みパラメータを見つけることである。もしそのような重みパラメータが見つかれば、CBOWモデルはコンテキストからターゲットをより正しく推測できるようになる。

このように CBOWモデルの本来の目的は、コンテキストからターゲットを正しく推測できるようになることである。

この目的を達成するために学習を進めると、副産物として単語の意味がエンコードされた「単語の分散表現」が得られる。

5.1.2 言語モデル

言語モデル（Language Model）は、単語の並びに対して確率を与える。
単語の並びに対して、それがどれだけ起こり得るのか、それがどれだけ自然な言語の並びであるのかということを確率で評価する。

言語モデルの例

たとえば、「you say goodbye」という単語の並びには高い確率（たとえば0.092）を出力し、「you say good die」という単語の並びには、低い確率（たとえば0.0000000000032）を出力するというようなことを行う。

この言語モデルは、機械翻訳や音声認識などのアプリケーションで利用できる。

たとえば、ある音声認識システムの場合、人の発話からいくつかの文章を候補として生成する。その場合、言語モデルを使えば、候補となる文章が「文章として自然であるかどうか」という基準でランク付けできる。

また、言語モデルは新しい文章を生成する用途にも利用できる。言語モデルは単語列の自然さを確率的に評価できるため、その確率分布に従って単語をサンプリングすることができる。

数式を使って言語モデルを記述

$w_1、・・・・w_m$というm個の単語からなる文章について考える。
このとき、$w_1、・・・・w_m$という順序で単語が出現する確率は、P($w_1$、・・・・、$w_{m}$)で表される。

この確率は複数の事象が同時に起こる確率であるため、同時確率と呼ばれる。
この同時確率P($w_1$、・・・・、$w_{m}$)は、事後確率を使って次のように分解して書くことができる。

式5.4

\begin{align}
P(w_1, \dots, w_{m}) & = P(w_m|w_1, \dots, w_{m-1})P(w_{m-1}|w_1, \dots, w_{m-2}) \dots \\
& \quad P(w_3|w_1, w_{2})P(w_2|w_1)P(w_1) \\
& =\prod_{t=1}^{m}P(w_t|w_1, \dots, w_{t-1})
\end{align}

-Π（パイ）は、全ての要素をかけ合わせる「総乗」を表す。

式5.4で示すとおり、同時確率は事後確率の総乗で表すことができる。

式5.4の結果は確率の乗法定理、P(A,B) = P(A|B)P(B)　から導くことができる。この定理は、「AとBの両方が起こる確率（P(A,B)」は、「bが起こる確率P(B)」と「bが起こった後にAが起こる確率P（A｜B）」を掛け合わせたものになる。

この乗法定理を使えば、m個の単語の同時確率$P(w_1、・・・・、w_{m} )$を事後確率であらわすことができる。

このとき行う式変形は、まず$w_1、・・・・、w_{m-1}$をまとめてAという記号で表す。

式5.6
$$
P(w_1、・・・・、w_{m-1}、w_{m}) = P(A, w_m) = P(w_{m}|A)P(A)
$$

続いて、この$A P(w_1、・・・・、w_{m-1})$ に対して、再び同じ式変形を行う。 $w_1、・・・、w_{m-2}$をまとめてA'という記号で表す。

式5.7
$$
P(w_1、・・・・、w_{m-2}、w_{m-1}) = P(A', w_{m-1}) = P(w_{m-1}|A)P(A)
$$

このように単語の並びをひとつずつ小さくしながら、その都度事後確率を分解していく。 後は同様の手順を繰り返すことで、式5.4が導かれる。

式5.4が示すように、目的とする同時確率の$P(|w_1、・・・・、w_{m})$は、事後確率の総和である$\prod_{t=1}^{m}P(w_t|w_1、・・・・、w_{t-1})$によって表すことができる。

ここで注目すべきは、その事後確率は、対象の単語より左側の全ての単語をコンテキスト（条件）とした確率であるということである。

ここまでのまとめ

目標は、$P(w_t|w_1、・・・・、w_{t-1})$という確率を得ることである。
その確率が計算できれば、言語モデルの同時確率$P(w_1、・・・・、w_{m})$を求めることができる。

5.1.3 CBOWモデルを言語モデルに？

word2vecのCBOWモデルを、（無理やり）言語モデルに適用する。
コンテキストのサイズをある値に限定することで、CBOWモデルによって、近似的に言語モデルを表すことができる。

これは数式で表すと次のようになる。

式5.8

$$
P(w_1、・・・・、w_{m}) = \prod_{t=1}^{m}P(w_t|w_1、・・・・、w_{t-1}) ≈ \prod_{t=1}^{t}P(w_t|w_{t-2}、w_{t-1})
$$

式5.8では、コンテキストとして２つの単語を用いる例を示した。
コンテキストのサイズは任意の長さに設定できるが、ある長さに固定する必要がある。

CBOWモデルの問題点

たとえば、左側の１０個の単語をコンテキストとしてCBOWモデルを作ると、そのコンテキストよりも左側にある単語の情報は無視されてしまう。

これは、下のような例で問題になる。
「Tom was watching TV in his room.　Mary came into the room. Mary said hi to ? 」

この問題では、「Tomが部屋でテレビを見ていて、Maryがその部屋に入ってきた」とある。

その文脈（コンテキスト）を踏まえると、Maryが「Tom」もしくは「him」に挨拶をするのが正解になる。ここで正しい答えを得るには例文の「?」から18個も前に登場するTomを記憶しておく必要がある。CBOWモデルのコンテキストが1７個以下の場合は、この問題を正しく答えることはできない。

CBOWモデルのコンテキストのサイズはいくらでも大きくすることができる。
しかし、CBOWモデルにはコンテキスト内の単語の並びが無視されるという問題がある。
具体例で説明すると、コンテキストとして2個の単語を扱う場合、CBOWモデルは単語の2個の単語ベクトルの「和」が中間層にくる。そのため、コンテキストの並び順は無視される。

本来であれば、コンテキストの並び順も考慮したモデルを望まれる。

これを達成するには、コンテキストの単語ベクトルを中間層において「連結(concatenate)」することが考えらえる。しかし、連結するアプローチをとったとしたら、コンテキストのサイズに比例して重みパラメータが増えてしまう。

この問題を解決するのが、リカレントニューラルネットワーク、略してRNNである。

RNNは、コンテキストがどれだけ長くても、そのコンテキストの情報を記憶するメカニズムを持つ。そのためRNNは、どんなに長い時系列データにも立ち向かうことができる。

5.2 RNNとは

RNN(Recurrent Neural Network)にあるRecurrentとはラテン語で「何度でも繰り返し起こること」を意味する。RNNを直訳すると、「再発するニューラルネットワーク」や「循環するニューラルネットワーク」になる。

5.2.1 循環するニューラルネットワーク

図5-1に示すとおりRNNは、ループする経路（閉じた経路）を持つ。
このループする経路によって、データがレイヤ内を循環することができる。
そしてデータが循環することにより、過去の情報を記憶しながら、最新データへと更新されていく。

図5-1 ループする経路を持つRNNレイヤ

図5-1では時刻をtとして、$x_t$を入力としている。これは時系列データとして、（$x_0、x_1...、x_t、...$）というデータがレイヤへ入力されることを示している。

そして、その入力に対応する形で、（$h_0、h_1...、h_t、...$）が出力される。

またここで、RNNレイヤへは各時刻に$x_t$が入力されるが、$x_t$は何らかのベクトルを想定する。

たとえば、文章を扱う場合、各単語の分散表現（単語ベクトル）を$x_t$として、それをRNNレイヤへ入力するようなケースがひとつの例である。

5.2.2 ループの展開

RNNレイヤのループ構造について詳しく見ていく。
RNNレイヤのループを展開することで、 フィードフォワード型と同じデータが一方向のニューラルネットワークに変身させることできる。

図5-2 RNNレイヤのループの展開

複数のRNNレイヤは、すべて「同じレイヤ」であることが、これまでのニューラルネットワークとは異なる。

各時刻のRNNレイヤは、そのレイヤへの入力とひとつ前のRNNからの出力を受け取る。
そして、その２つの情報を元に、その時刻の出力が計算される。
このとき行う計算を数式で表したのが、式5.9である。

式5.9

$$
h_t = tanh(h_{t-1}W_h + x_tW_x + b)
$$

• $W_x$は、入力xを出力hに変換するための重み。
• $W_h$は、ひとつ前のRNNの出力を次時刻の出力に変換するための重み。
• bはバイアス。
• $h_{t-1}$と$x_t$は行ベクトル。
• $h_t$：時刻tの出力。行列の内積による計算を行い、それらの和をtanh関数によって変換した結果。

この$h_t$は、別のレイヤに向けて上方向へ出力されると同時に、次時刻のRNNレイヤに向けて右方向へも出力される。

5.2.3 Backpropagation Through Time

ループを展開した後のRNNは、通常のニューラルネットワークと同様に誤差逆伝播法を用いることができる。
ここでの誤差逆伝播法は時間方向に展開したニューラルネットワークの誤差逆伝播法ということで、BPTT(Backpropagation Through Time)と呼ばれる。

また、RNNレイヤを計算グラフで表現すると図5-3のようになる。

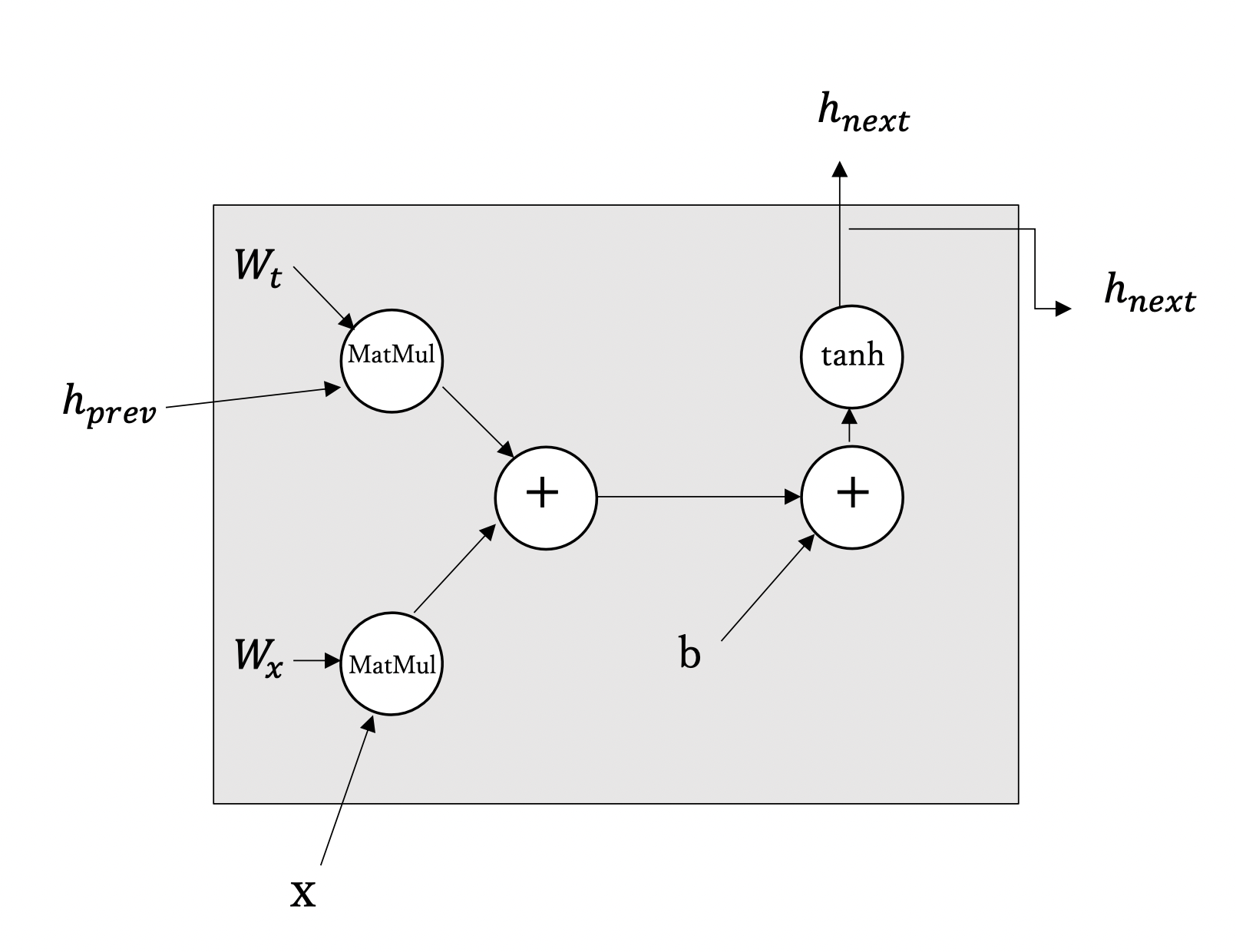
図5-3 RNNレイヤの計算グラフ（MatMulノードは行列の積を表す）

BPTTの問題点

長い時系列データを学習する際は、BPTTで消費するコンピュータの計算リソースが膨大になってしまう。
BPTTによって勾配を求めるには、各時刻のRNNレイヤの中間データを保持する必要があるので、時系列データが長くなるとメモリ使用量も増加する。

また、時間サイズが長くなると、逆伝播時の勾配が不安定になることも問題になる。

5.2.4 Truncated BPTT

大きな時系列データを扱うときによく行われるのが、ある一定の長さでネットワークの繋がりを断ち切ることである。正確には、ネットワークの逆伝播の繋がりだけを断ち切る。
順伝播の流れは途切れることなく伝播させ、逆伝播のつながりは適当な長さで切り取り、その切り取られたネットワーク単位で学習を行う。

これが、Truncated BPTTと呼ばれる手法である。

順伝播は切断させないため、RNNの学習を行う際はデータを順番に（シーケンシャルに）与える必要がある。

例えば時系列データが1000個の単語が並んだコーパスの場合、RNNレイヤを展開すると横方向に1000個のレイヤが並んだネットワークになる。 　
コーパスを１０語単位で切って逆伝播のつながりを断てば、それより先のデータ（文章）について考える必要がなくなる。
順伝播は次のブロックに、隠れ層$h_{t-1}$を引き継ぎながら学習を行う。

TruncatedBPTTによるRNNの学習の流れ

1 . 0〜9番目の単語

• 順伝播: $h_0, \dots, h_9$ を計算し、$h_9$を10〜19番目の単語の順伝播に引き継ぐ。

• 逆伝播: $dh_9, \dots, dh_0$ を計算し、$dx_9, \dots, dx_0$ を更新する。

2 . 10〜19番目の単語

• 順伝播: $h_9$ を引き継ぎ、$h_{10}, \dots, h_{19}$ を計算し、$h_{19}$を20〜29番目の単語の順伝播に引き継ぐ。

• 逆伝播: $dh_{19}, \dots, dh_{10}$ を計算し、$dx_{19}, \dots, dx_{10}$ を更新する

3 . ・・・

5.2.5 Truncated BPTTのミニバッチ学習

Truncated BPTTのミニバッチ学習を行うためにはバッチを考慮して、シーケンシャルにデータを与える必要がある （Truncated BPTTでミニバッチ学習する際、データをランダムに選ぶことはしない）。
そのために、データを与える開始位置をズラす必要がある。

1000個の単語が並んだコーパスを10語ずつ切って、ミニバッチのバッチ数を2として学習するにはどうしたら良いだろうか。

その場合、RNNレイヤの入力データとして、1つ目のバッチには、先頭から順に
データを１０個ずつ与えていき、2つ目のバッチには、500番目のデータを開始位置としてそこから順にデータを１０個ずつ与えていく必要がある。

つまり、開始位置を500だけズラすということになる。
すなわち、batch毎に見ると

長い時系列データを処理するとき、RNNの隠れ状態を維持する必要がある。
このような隠れ状態を維持する機能はstatefulという言葉で表現され、多くのディープラーニングのフレームワークの引数としてstatefulが存在している。

5.3 RNNの実装

RNN言語モデル（RNNLM）全体のイメージを掴んでから、各レイヤを実装していく。

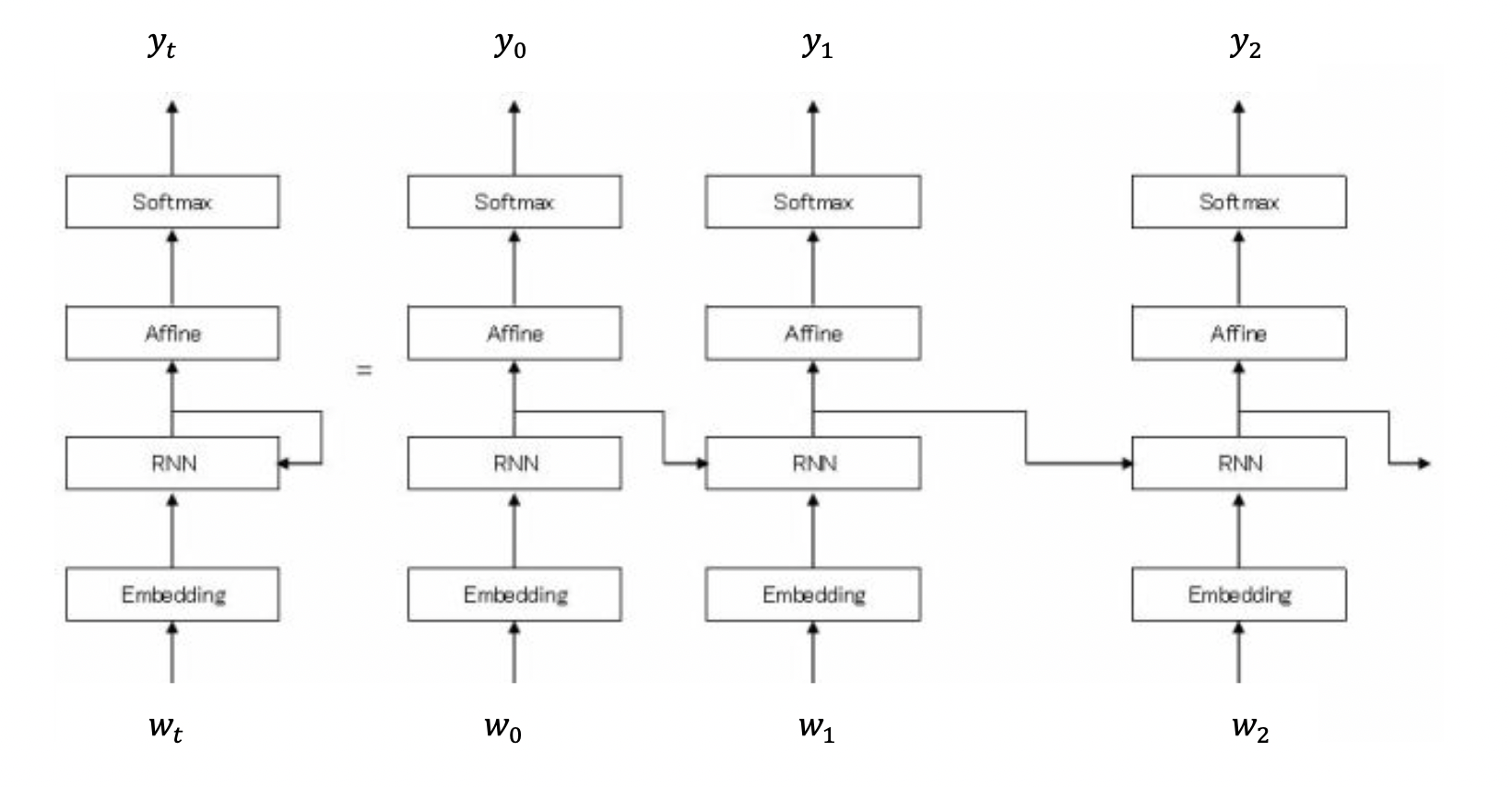
図5-4 RNN言語モデル（RNNLM）全体の構造のイメージ

最初の層はEmbeddingレイヤとなっており、単語IDを単語の分散表現（単語ベクトル）へと変換する。

そしてその分散表現が、RNNレイヤへと入力される。このRNNレイヤは隠れ状態を次の層へ（図でいうと上方向）出力すると同時に、次時刻のRNNレイヤへ（図でいうと右方向）出力する。

そして、RNNレイヤが上方向に出力した隠れ状態は、Affineレイヤ（全結合層）を経て、Softmaxレイヤと伝わり、確率が出力される。

5.3.1 RNNレイヤの実装

まず、RNNの1ステップを行うRNNクラスを実装する。そして、RNNクラスを利用して、Tステップ分をまとめて行うTimeRNNクラスを実装する。

RNNの順伝播の式の再掲

$$
h_t = tanh(h_{t-1}W_h + x_tW_x + b)
$$

ミニバッチとしてデータをまとめて処理するので、$x_t$（と$h_t$）には各サンプルデータを行方向に格納する。

なお、行列の計算においては行列の「形状チェック」が重要である。

\begin{align*}
h_{t-1} W_h &+ x_t W_x &= &h_t\\
N×H\>{H×H} &+N×D\>{D×H} &= &N×H
\end{align*}

N：バッチサイズ
D：入力ベクトルの次元数
H：隠れ状態ベクトルの次元数

class RNN:
    def __init__(self, Wx, Wh, b):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.cache = None

    def forward(self, x, h_prev):
        Wx, Wh, b = self.params
        t = np.dot(h_prev, Wh) + np.dot(x, Wx) + b
        h_next = np.tanh(t)

        self.cache = (x, h_prev, h_next)
        return h_next

    def backward(self, dh_next):
        Wx, Wh, b = self.params
        x, h_prev, h_next = self.cache

        dt = dh_next * (1 - h_next ** 2)
        db = np.sum(dt, axis=0)
        dWh = np.dot(h_prev.T, dt)
        dh_prev = np.dot(dt, Wh.T)
        dWx = np.dot(x.T, dt)
        dx = np.dot(dt, Wx.T)

        self.grads[0][...] = dWx
        self.grads[1][...] = dWh
        self.grads[2][...] = db

        return dx, dh_prev

1. init：引数として重みを２つとバイアスを受け取る。ここでは、引数で渡されたパラメータをメンバ変数のparamsにリストとして設定する。そして、各パラメータに対応する形で勾配を初期化し、それをgradsに格納する。最後に、逆伝播の計算どきに使用する中間データをcacheとして、これをNoneで初期化する。

2. forward：引数として、下からの入力xと、左からの入力h_prevを受け取る。後は、RNNの順伝播の式（$h_t = tanh(h_{t-1}W_h + x_tW_x + b)$）に沿って実装する。

3. backward：次の隠れ状態h_nextの勾配dh_nextを受け取り、パラメータWx, Wh, bに関する勾配（dWx, dWh, db）および入力xと前の隠れ状態h_prevに関する勾配（dx, dh_prev）を計算して返す。
   計算された勾配はgradsに更新される。

図5-3の再掲 RNNレイヤの計算グラフ（MatMulノードは行列の積を表す）

5.3.2 Time RNNレイヤの実装

TimeRNNは、T個のRNNレイヤを連結したネットワークである（Tは任意の数に設定）。
xs=$(x_0,x_1,・・・,x_{T-1})$→Time RNNレイヤ→hs=$(h_0,h_1,・・・,h_{T-1})$

RNNレイヤの隠れ状態hをメンバ変数に保持する。 　
xs0→TimeRNNレイヤ→hs0 （hをTimeRNNクラスのメンバ変数に保持）
h, xs1→TimeRNNレイヤ→hs1 ・・・

class TimeRNN:
    def __init__(self, Wx, Wh, b, stateful=False):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
        self.layers = None

        self.h, self.dh = None, None
        self.stateful = stateful

    def forward(self, xs):
        Wx, Wh, b = self.params
        N, T, D = xs.shape
        D, H = Wx.shape

        self.layers = []
        hs = np.empty((N, T, H), dtype='f')

        if not self.stateful or self.h is None:
            self.h = np.zeros((N, H), dtype='f')

        for t in range(T):
            layer = RNN(*self.params)
            self.h = layer.forward(xs[:, t, :], self.h)
            hs[:, t, :] = self.h
            self.layers.append(layer)

        return hs

    def backward(self, dhs):
        Wx, Wh, b = self.params
        N, T, H = dhs.shape
        D, H = Wx.shape

        dxs = np.empty((N, T, D), dtype='f')
        dh = 0
        grads = [0, 0, 0]
        for t in reversed(range(T)):
            layer = self.layers[t]
            dx, dh = layer.backward(dhs[:, t, :] + dh)
            dxs[:, t, :] = dx

            for i, grad in enumerate(layer.grads):
                grads[i] += grad

        for i, grad in enumerate(grads):
            self.grads[i][...] = grad
        self.dh = dh

        return dxs

    def set_state(self, h):
        self.h = h

    def reset_state(self):
        self.h = None

1. init: このメソッドはクラスの初期化を行う。
   パラメータ（Wx, Wh, b）および勾配（grads）を初期化し、隠れ状態hとその勾配dhを設定。また、stateful（状態保持）オプションを設定で切る。

2. forward:入力シーケンスxsを受け取り、各時刻の隠れ状態hsを計算して返す。RNNクラスのインスタンスを各時刻で生成し、layersリストに追加していく。

3. backward: 隠れ状態hsの勾配dhsを受け取り、入力シーケンスxsに関する勾配dxsを計算して返す。 各時刻のRNNインスタンスに対して逆伝播を行い、勾配を累積して更新する。

4. set_state: 隠れ状態hを設定する。

5. reset_state: 隠れ状態hをリセット（Noneに設定）する。

5.4.2 Timeレイヤの実装

Google ColabでGPUを使用するには、まず「ランタイム」メニューから「ランタイムのタイプを変更」を選択し、ハードウェアアクセラレータとしてGPUを選択。

「!pip list」を実行すると、cupy-cuda11x のver11.0.0」が、既にインストールされていることが分かる。

!pip list

5.4 時系列データを扱うレイヤの実装

5.4.1 Timeレイヤの実装

TimeEmbeddingクラス:

TimeEmbeddingクラスは、それぞれEmbedding層を時間方向に展開したもの

import cupy as np
class Embedding:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.idx = None

    def forward(self, idx):
        W, = self.params
        self.idx = idx
        out = W[idx]
        return out

    def backward(self, dout):
        dW, = self.grads
        dW[...] = 0
        """
        scatter_add()は、現在のcupyバージョンではサポートされていない。
        調べたら、_cupyx.scatter_add()を使って実装している人が多かったので採用した。
        """
        np._cupyx.scatter_add(dW, self.idx, dout) #gpu
        # np.add.at(dW, self.idx, dout) #not gpu
        return None

forward: 入力シーケンスxsを受け取り、埋め込み表現outを計算して返す。
各時刻に対してEmbeddingクラスのインスタンスを生成し、layersリストに追加していく。

backward: 埋め込み表現outの勾配doutを受け取り、パラメータWに関する勾配を計算して返す
各時刻のEmbeddingインスタンスに対して逆伝播を行い、勾配を累積して更新する。

TimeAffineクラス:

TimeAffineクラスはAffine（全結合）層を時間方向に展開したもの。

class TimeAffine:
    def __init__(self, W, b):
        self.params = [W, b]
        self.grads = [np.zeros_like(W), np.zeros_like(b)]
        self.x = None

    def forward(self, x):
        N, T, D = x.shape
        W, b = self.params

        rx = x.reshape(N*T, -1)
        out = np.dot(rx, W) + b
        self.x = x
        return out.reshape(N, T, -1)

    def backward(self, dout):
        x = self.x
        N, T, D = x.shape
        W, b = self.params

        dout = dout.reshape(N*T, -1)
        rx = x.reshape(N*T, -1)

        db = np.sum(dout, axis=0)
        dW = np.dot(rx.T, dout)
        dx = np.dot(dout, W.T)
        dx = dx.reshape(*x.shape)

        self.grads[0][...] = dW
        self.grads[1][...] = db

        return dx

forward: 入力xを受け取り、アフィン変換を適用した出力を計算して返す。
入力xの形状を変更し、アフィン変換を適用した後、出力の形状を元に戻す。

backward: アフィン変換後の出力の勾配doutを受け取り、入力x、重みW、バイアスbに関する勾配を計算して返す。
勾配の計算には、順伝播時に保存された入力xが使用される。

TimeSoftmaxWithLossクラス

Softmax関数と損失関数（交差エントロピー誤差）を時間方向に展開したもの。
出力層に使用され、モデルの予測精度を評価するために損失を計算する。

Time Softmax With Lossレイヤを数式で表す

$$
L_0,L_1,\dots,L_{T-1} = Softmax with Loss(x_0,t_0),Softmax with Loss(x_1,t_1),\dots,Softmax with Loss(x_{T-1},t_{T-1})
$$

x：下の層から伝わるスコア。スコアとは、確率へと正規化される前の値。
t：正解ラベル

$$
L=(L_0+L_1+\dots+L_{T-1})×\frac{1}{T}
$$

T個のSoftmaxWithLossレイヤのそれぞれの損失を算出→合算→平均を取る＝最終的な損失とする。

Time Softmax With Lossレイヤの処理フロー

xs,xt → Time Softmax with Lossレイヤ → L

Softmax関数：

def softmax(x):
    if x.ndim == 2:
        x = x - x.max(axis=1, keepdims=True)
        x = np.exp(x)
        x /= x.sum(axis=1, keepdims=True)
    elif x.ndim == 1:
        x = x - np.max(x)
        x = np.exp(x) / np.sum(np.exp(x))

    return x

TimeSoftmaxWithLossレイヤ：

class TimeSoftmaxWithLoss:
    def __init__(self):
        self.params, self.grads = [], []
        self.cache = None
        self.ignore_label = -1

    def forward(self, xs, ts):
        N, T, V = xs.shape

        if ts.ndim == 3:  # 教師ラベルがone-hotベクトルの場合
            ts = ts.argmax(axis=2)

        mask = (ts != self.ignore_label)

        # バッチ分と時系列分をまとめる（reshape）
        xs = xs.reshape(N * T, V)
        ts = ts.reshape(N * T)
        mask = mask.reshape(N * T)

        ys = softmax(xs)
        ls = np.log(ys[np.arange(N * T), ts])
        ls *= mask  # ignore_labelに該当するデータは損失を0にする
        loss = -np.sum(ls)
        loss /= mask.sum()

        self.cache = (ts, ys, mask, (N, T, V))
        return loss

    def backward(self, dout=1):
        ts, ys, mask, (N, T, V) = self.cache

        dx = ys
        dx[np.arange(N * T), ts] -= 1
        dx *= dout
        dx /= mask.sum()
        dx *= mask[:, np.newaxis]  # ignore_labelに該当するデータは勾配を0にする

        dx = dx.reshape((N, T, V))

        return dx

init: パラメータと勾配のリストを空にし、キャッシュをNoneに設定する。また、無視するラベルを-1に設定する。

forward: 入力xsと教師ラベルtsを受け取り、損失を計算して返す。xsとtsは、T個分の時系列データを一つにまとめたもの。教師ラベルがone-hotベクトルの場合、インデックスに変換する。また、無視するラベルに対応するデータの損失を0に設定する。計算された情報は後で逆伝播の際に利用するためキャッシュに保存される。

backward: 損失の勾配（通常は1）を受け取り、入力xsに関する勾配dxを計算して返す。無視するラベルに対応するデータの勾配を0に設定する。

SimpleRNNの実装：

class SimpleRnnlm:
    def __init__(self, vocab_size, wordvec_size, hidden_size):
        V, D, H = vocab_size, wordvec_size, hidden_size
        rn = np.random.randn

        # 重みの初期化
        embed_W = (rn(V, D) / 100).astype('f')
        rnn_Wx = (rn(D, H) / np.sqrt(D)).astype('f')
        rnn_Wh = (rn(H, H) / np.sqrt(H)).astype('f')
        rnn_b = np.zeros(H).astype('f')
        affine_W = (rn(H, V) / np.sqrt(H)).astype('f')
        affine_b = np.zeros(V).astype('f')

        # レイヤの生成
        self.layers = [
            TimeEmbedding(embed_W),
            TimeRNN(rnn_Wx, rnn_Wh, rnn_b, stateful=True),
            TimeAffine(affine_W, affine_b)
        ]
        self.loss_layer = TimeSoftmaxWithLoss()
        self.rnn_layer = self.layers[1]

        # すべての重みと勾配をリストにまとめる
        self.params, self.grads = [], []
        for layer in self.layers:
            self.params += layer.params
            self.grads += layer.grads

    def forward(self, xs, ts):
        for layer in self.layers:
            xs = layer.forward(xs)
        loss = self.loss_layer.forward(xs, ts)
        return loss

    def backward(self, dout=1):
        dout = self.loss_layer.backward(dout)
        for layer in reversed(self.layers):
            dout = layer.backward(dout)
        return dout

    def reset_state(self):
        self.rnn_layer.reset_state()

init: 引数として語彙数(vocab_size)、単語ベクトルの次元数(wordvec_size)、隠れ層のサイズ(hidden_size)を受け取る。各層の重みとバイアスを初期化し、TimeEmbedding, TimeRNN, TimeAffineのインスタンスを生成する。また、TimeSoftmaxWithLossのインスタンスを損失層として設定する。

forward: 入力xsと正解ラベルtsを受け取り、損失を計算して返す。順伝播は各層を順番に通して行われる。

backward: 損失の勾配（通常は1）を受け取り、各パラメータに関する勾配を計算する。逆伝播は各層を逆順に通して行われる。

reset_state: RNN層の状態をリセットする。これは、時系列データを扱う際に、異なるシーケンス間で状態を共有しないために使用される。

5.5.2 言語モデルの評価

言語モデルでは、過去の与えられた単語（情報）から次に出現する単語の確率分布を出力する。言語モデルの予測性能の良さを評価する指標として、パープレキシティ(perplexity)を用いる。

パープレキシティは、データ数がひとつのときは確率の逆数である。
パープレキシティは小さければ小さいほどよい。

データ数がひとつのときのパープレキシティの例

たとえば、「you say goodbye and I say hello.」というコーパスを考える。
　
youを言語モデルに与えて、出力された確率分布のsayが0.8の確率だった場合は、良い予測と言える。このときのパープレキシティは、その確率の逆数をとって$\frac{1}{0.8}=1.25$と計算できる。

youを言語モデルに与えて、出力された確率分布のsayが0.2の確率だった場合は、悪い予測と言える。このときのパープレキシティは、その確率の逆数をとって$\frac{1}{0.2}=5.0$と計算できる。

パープレキシティの値は、分岐数と解釈することができる。分岐数とは、次に出現しうる単語の候補の数である。 　

1.25→次に出現する候補が１個
5.0 →次に出現する候補が5個

入力のデータが複数の場合のパープレキシティ

式5.12
$$
L = \frac{1}{N}\sum_{n}\sum_{k}t_{nk}logy_{nk}
$$
$$
perplexity = e^L
$$
N:データ
$t_{n}$：one-hotベクトルの正解ラベル
$t_{nk}$：nコメのデータのk番目の値
$y_{nk}$： 確率分布
L：ニューラルネットワークの損失

Lを使って、eのL乗を計算したものが、パープレキシティになる。

パープレキシティのまとめ

パープレキシティの直感的な理解は、確率の逆数である。
パープレキシティが小さくなろほど、分岐数が減り良いモデルである。

5.5.3 RNNLMの学習コード

PTBデータセットを取得

pip install nltk

import nltk
nltk.download('treebank')
from nltk.corpus import treebank

# PTBデータセットを取得する
ptb = ' '.join(treebank.words())

データの前処理

def preprocess(text):
  text = text.lower()
  text = text.replace('.', ' .')
  words = text.split(' ')

  word_to_id = {}
  id_to_word = {}
  for word in words:
    if word not in word_to_id:
      new_id = len(word_to_id)
      word_to_id[word] = new_id
      id_to_word[new_id] = word
  
  corpus = np.array([word_to_id[w] for w in words])

  return corpus, word_to_id, id_to_word

勾配降下法
SGD（確率的勾配降下法（Stochastic Gradient Descent））を使う

class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr
        
    def update(self, params, grads):
        for i in range(len(params)):
            params[i] -= self.lr * grads[i]


class Momentum:
    '''
    Momentum SGD
    '''
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = []
            for param in params:
                self.v.append(np.zeros_like(param))

        for i in range(len(params)):
            self.v[i] = self.momentum * self.v[i] - self.lr * grads[i]
            params[i] += self.v[i]

PTBデータと勾配降下法の実装の用意ができた。
ここから、PTBデータを使ってRNNLMの学習を行う。
ここで実装するRNNLMでは、すべtの訓練データを対象にすると良い結果が得られないので、PTBデータセット（訓練データ）の先頭の1000個の単語を利用する。

import matplotlib.pyplot as plt
# import numpy as np


# ハイパーパラメータの設定
batch_size = 10
wordvec_size = 100
hidden_size = 100
time_size = 5  # Truncated BPTTの展開する時間サイズ
lr = 0.1
max_epoch = 100

# 学習データの読み込み（データセットを小さくする）
corpus, word_to_id, id_to_word = preprocess(ptb)
corpus_size = 1000
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus) + 1)

xs = corpus[:-1]  # 入力
ts = corpus[1:]  # 出力（教師ラベル）
data_size = len(xs)
print('corpus size: %d, vocabulary size: %d' % (corpus_size, vocab_size))

# 学習時に使用する変数
max_iters = data_size // (batch_size * time_size)
time_idx = 0
total_loss = 0
loss_count = 0
ppl_list = []

# モデルの生成
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)

# ミニバッチの各サンプルの読み込み開始位置を計算
jump = (corpus_size - 1) // batch_size
offsets = [i * jump for i in range(batch_size)]

for epoch in range(max_epoch):
    for iter in range(max_iters):
        # ミニバッチの取得
        batch_x = np.empty((batch_size, time_size), dtype='i')
        batch_t = np.empty((batch_size, time_size), dtype='i')
        for t in range(time_size):
            for i, offset in enumerate(offsets):
                batch_x[i, t] = xs[(offset + time_idx) % data_size]
                batch_t[i, t] = ts[(offset + time_idx) % data_size]
            time_idx += 1

        # 勾配を求め、パラメータを更新
        loss = model.forward(batch_x, batch_t)
        model.backward()
        optimizer.update(model.params, model.grads)
        total_loss += loss
        loss_count += 1

    # エポックごとにパープレキシティの評価
    ppl = np.exp(total_loss / loss_count)
    print('| epoch %d | perplexity %.2f'
          % (epoch+1, ppl))
    ppl_list.append(float(ppl))
    total_loss, loss_count = 0, 0

# グラフの描画
x = np.arange(len(ppl_list))
"""
ppl_listの描画でエラーが出たので、CuPy配列をNumPy配列に変換した。
TypeError: Implicit conversion to a NumPy array is not allowed. Please use `.get()` to construct a NumPy array explicitly.
"""
ppl_list_np = [elem.get() if isinstance(elem, np.ndarray) else elem for elem in ppl_list]
plt.plot(x.get(), ppl_list_np, label='train')
plt.xlabel('epochs')
plt.ylabel('perplexity')
plt.show()

"""
corpus size: 1000, vocabulary size: 431
| epoch 1 | perplexity 406.08
| epoch 2 | perplexity 291.12
| epoch 3 | perplexity 245.26
| epoch 4 | perplexity 225.04
| epoch 5 | perplexity 222.06
| epoch 6 | perplexity 212.34
| epoch 7 | perplexity 213.86
| epoch 8 | perplexity 209.79
| epoch 9 | perplexity 204.43
| epoch 10 | perplexity 203.59
| epoch 11 | perplexity 195.51
| epoch 12 | perplexity 196.72
| epoch 13 | perplexity 192.70
| epoch 14 | perplexity 193.03
| epoch 15 | perplexity 187.89
| epoch 16 | perplexity 184.83
| epoch 17 | perplexity 179.05
| epoch 18 | perplexity 180.02
| epoch 19 | perplexity 175.22
| epoch 20 | perplexity 168.10
| epoch 21 | perplexity 165.09
| epoch 22 | perplexity 159.26
| epoch 23 | perplexity 160.10
| epoch 24 | perplexity 153.91
| epoch 25 | perplexity 149.71
| epoch 26 | perplexity 144.70
| epoch 27 | perplexity 145.19
| epoch 28 | perplexity 138.55
| epoch 29 | perplexity 133.22
| epoch 30 | perplexity 132.52
| epoch 31 | perplexity 123.16
| epoch 32 | perplexity 119.72
| epoch 33 | perplexity 117.96
| epoch 34 | perplexity 115.11
| epoch 35 | perplexity 107.87
| epoch 36 | perplexity 105.13
| epoch 37 | perplexity 99.59
| epoch 38 | perplexity 96.06
| epoch 39 | perplexity 93.24
| epoch 40 | perplexity 86.16
| epoch 41 | perplexity 84.23
| epoch 42 | perplexity 78.73
| epoch 43 | perplexity 76.49
| epoch 44 | perplexity 72.41
| epoch 45 | perplexity 67.91
| epoch 46 | perplexity 64.88
| epoch 47 | perplexity 62.15
| epoch 48 | perplexity 60.21
| epoch 49 | perplexity 55.88
| epoch 50 | perplexity 52.91
| epoch 51 | perplexity 49.67
| epoch 52 | perplexity 46.86
| epoch 53 | perplexity 43.87
| epoch 54 | perplexity 43.31
| epoch 55 | perplexity 39.62
| epoch 56 | perplexity 38.02
| epoch 57 | perplexity 34.46
| epoch 58 | perplexity 34.07
| epoch 59 | perplexity 31.79
| epoch 60 | perplexity 31.35
| epoch 61 | perplexity 28.69
| epoch 62 | perplexity 27.93
| epoch 63 | perplexity 26.79
| epoch 64 | perplexity 24.54
| epoch 65 | perplexity 22.93
| epoch 66 | perplexity 22.01
| epoch 67 | perplexity 20.74
| epoch 68 | perplexity 19.70
| epoch 69 | perplexity 19.12
| epoch 70 | perplexity 17.72
| epoch 71 | perplexity 17.07
| epoch 72 | perplexity 16.05
| epoch 73 | perplexity 14.71
| epoch 74 | perplexity 14.55
| epoch 75 | perplexity 14.62
| epoch 76 | perplexity 13.02
| epoch 77 | perplexity 12.94
| epoch 78 | perplexity 12.60
| epoch 79 | perplexity 11.65
| epoch 80 | perplexity 11.45
| epoch 81 | perplexity 10.87
| epoch 82 | perplexity 10.58
| epoch 83 | perplexity 10.24
| epoch 84 | perplexity 9.32
| epoch 85 | perplexity 8.46
| epoch 86 | perplexity 8.34
| epoch 87 | perplexity 8.09
| epoch 88 | perplexity 7.96
| epoch 89 | perplexity 7.08
| epoch 90 | perplexity 6.78
| epoch 91 | perplexity 6.78
| epoch 92 | perplexity 6.98
| epoch 93 | perplexity 5.93
| epoch 94 | perplexity 5.82
| epoch 95 | perplexity 5.65
| epoch 96 | perplexity 5.38
| epoch 97 | perplexity 5.34
| epoch 98 | perplexity 5.12
| epoch 99 | perplexity 5.10
| epoch 100 | perplexity 4.80
"""

5.5.4 RNNLMのTrainerクラス

次のような処理を行う RnnlmTrainer クラスを作成する。

• mini-batch を sequential に作成する
• model のforward() と backward() を呼び出す。
• Optimizer でtrainingする (𝑊のweight を調整する)
• perplexity を計算する。

def clip_grads(grads, max_norm):
    total_norm = 0
    for grad in grads:
        total_norm += np.sum(grad ** 2)
    total_norm = np.sqrt(total_norm)

    rate = max_norm / (total_norm + 1e-6)
    if rate < 1:
        for grad in grads:
            grad *=  rate

def remove_duplicate(params, grads):
    '''
    パラメータ配列中の重複する重みをひとつに集約し、
    その重みに対応する勾配を加算する
    '''
    params, grads = params[:], grads[:]  # copy list

    while True:
        find_flg = False
        L = len(params)

        for i in range(0, L - 1):
            for j in range(i + 1, L):
                # 重みを共有する場合
                if params[i] is params[j]:
                    grads[i] += grads[j]  # 勾配の加算
                    find_flg = True
                    params.pop(j)
                    grads.pop(j)
                # 転置行列として重みを共有する場合（weight tying）
                elif params[i].ndim == 2 and params[j].ndim == 2 and \
                     params[i].T.shape == params[j].shape and np.all(params[i].T == params[j]):
                    grads[i] += grads[j].T
                    find_flg = True
                    params.pop(j)
                    grads.pop(j)

                if find_flg: break
            if find_flg: break

        if not find_flg: break

    return params, grads

RnnlmTrainerクラス：

import numpy
import time
import matplotlib.pyplot as plt

class RnnlmTrainer:
    def __init__(self, model, optimizer):
        self.model = model
        self.optimizer = optimizer
        self.time_idx = None
        self.ppl_list = None
        self.eval_interval = None
        self.current_epoch = 0

    def get_batch(self, x, t, batch_size, time_size):
        batch_x = np.empty((batch_size, time_size), dtype='i')
        batch_t = np.empty((batch_size, time_size), dtype='i')

        data_size = len(x)
        jump = data_size // batch_size
        offsets = [i * jump for i in range(batch_size)]  # バッチの各サンプルの読み込み開始位置

        for time in range(time_size):
            for i, offset in enumerate(offsets):
                batch_x[i, time] = x[(offset + self.time_idx) % data_size]
                batch_t[i, time] = t[(offset + self.time_idx) % data_size]
            self.time_idx += 1
        return batch_x, batch_t

    def fit(self, xs, ts, max_epoch=10, batch_size=20, time_size=35,
            max_grad=None, eval_interval=20):
        data_size = len(xs)
        max_iters = data_size // (batch_size * time_size)
        self.time_idx = 0
        self.ppl_list = []
        self.eval_interval = eval_interval
        model, optimizer = self.model, self.optimizer
        total_loss = 0
        loss_count = 0

        start_time = time.time()
        for epoch in range(max_epoch):
            for iters in range(max_iters):
                batch_x, batch_t = self.get_batch(xs, ts, batch_size, time_size)

                # 勾配を求め、パラメータを更新
                loss = model.forward(batch_x, batch_t)
                model.backward()
                params, grads = remove_duplicate(model.params, model.grads)  # 共有された重みを1つに集約
                if max_grad is not None:
                    clip_grads(grads, max_grad)
                optimizer.update(params, grads)
                total_loss += loss
                loss_count += 1

                # パープレキシティの評価
                if (eval_interval is not None) and (iters % eval_interval) == 0:
                    ppl = np.exp(total_loss / loss_count)
                    elapsed_time = time.time() - start_time
                    print('| epoch %d |  iter %d / %d | time %d[s] | perplexity %.2f'
                          % (self.current_epoch + 1, iters + 1, max_iters, elapsed_time, ppl))
                    self.ppl_list.append(float(ppl))
                    total_loss, loss_count = 0, 0

            self.current_epoch += 1

    def plot(self, ylim=None):
        x = numpy.arange(len(self.ppl_list))
        if ylim is not None:
            plt.ylim(*ylim)
        plt.plot(x, self.ppl_list, label='train')
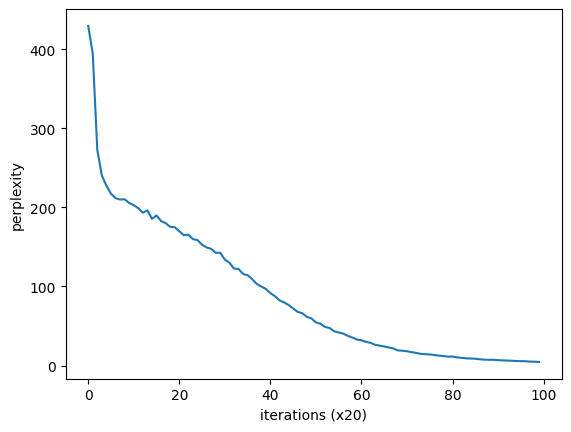
        plt.xlabel('iterations (x' + str(self.eval_interval) + ')')
        plt.ylabel('perplexity')
        plt.show()

RnnlmTrainerクラスを使ったRNNLMの学習

# ハイパーパラメータの設定
batch_size = 10
wordvec_size = 100
hidden_size = 100  # RNNの隠れ状態ベクトルの要素数
time_size = 5  # RNNを展開するサイズ
lr = 0.1
max_epoch = 100

# 学習データの読み込み
corpus, word_to_id, id_to_word = preprocess(ptb)
corpus_size = 1000  # テスト用にデータセットを小さくする
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus) + 1)
xs = corpus[:-1]  # 入力
ts = corpus[1:]  # 出力（教師ラベル）

# モデルの生成
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
trainer = RnnlmTrainer(model, optimizer)

trainer.fit(xs, ts, max_epoch, batch_size, time_size)
trainer.plot()
"""
| epoch 1 |  iter 1 / 19 | time 3[s] | perplexity 429.38
| epoch 2 |  iter 1 / 19 | time 3[s] | perplexity 394.36
| epoch 3 |  iter 1 / 19 | time 3[s] | perplexity 272.47
| epoch 4 |  iter 1 / 19 | time 3[s] | perplexity 240.11
| epoch 5 |  iter 1 / 19 | time 4[s] | perplexity 227.42
| epoch 6 |  iter 1 / 19 | time 4[s] | perplexity 217.28
| epoch 7 |  iter 1 / 19 | time 4[s] | perplexity 211.57
| epoch 8 |  iter 1 / 19 | time 4[s] | perplexity 209.88
| epoch 9 |  iter 1 / 19 | time 4[s] | perplexity 210.14
| epoch 10 |  iter 1 / 19 | time 5[s] | perplexity 205.51
| epoch 11 |  iter 1 / 19 | time 5[s] | perplexity 202.70
| epoch 12 |  iter 1 / 19 | time 5[s] | perplexity 198.84
| epoch 13 |  iter 1 / 19 | time 5[s] | perplexity 193.23
| epoch 14 |  iter 1 / 19 | time 5[s] | perplexity 196.11
| epoch 15 |  iter 1 / 19 | time 6[s] | perplexity 185.46
| epoch 16 |  iter 1 / 19 | time 6[s] | perplexity 189.70
| epoch 17 |  iter 1 / 19 | time 6[s] | perplexity 182.65
| epoch 18 |  iter 1 / 19 | time 6[s] | perplexity 180.03
| epoch 19 |  iter 1 / 19 | time 6[s] | perplexity 175.34
| epoch 20 |  iter 1 / 19 | time 6[s] | perplexity 174.80
| epoch 21 |  iter 1 / 19 | time 7[s] | perplexity 169.76
| epoch 22 |  iter 1 / 19 | time 7[s] | perplexity 164.75
| epoch 23 |  iter 1 / 19 | time 7[s] | perplexity 165.43
| epoch 24 |  iter 1 / 19 | time 7[s] | perplexity 159.74
| epoch 25 |  iter 1 / 19 | time 7[s] | perplexity 158.56
| epoch 26 |  iter 1 / 19 | time 7[s] | perplexity 152.64
| epoch 27 |  iter 1 / 19 | time 7[s] | perplexity 149.29
| epoch 28 |  iter 1 / 19 | time 8[s] | perplexity 147.48
| epoch 29 |  iter 1 / 19 | time 8[s] | perplexity 142.46
| epoch 30 |  iter 1 / 19 | time 8[s] | perplexity 142.67
| epoch 31 |  iter 1 / 19 | time 8[s] | perplexity 133.86
| epoch 32 |  iter 1 / 19 | time 8[s] | perplexity 130.01
| epoch 33 |  iter 1 / 19 | time 8[s] | perplexity 122.56
| epoch 34 |  iter 1 / 19 | time 8[s] | perplexity 122.09
| epoch 35 |  iter 1 / 19 | time 9[s] | perplexity 115.66
| epoch 36 |  iter 1 / 19 | time 9[s] | perplexity 114.25
| epoch 37 |  iter 1 / 19 | time 9[s] | perplexity 109.22
| epoch 38 |  iter 1 / 19 | time 9[s] | perplexity 103.19
| epoch 39 |  iter 1 / 19 | time 9[s] | perplexity 99.88
| epoch 40 |  iter 1 / 19 | time 9[s] | perplexity 96.84
| epoch 41 |  iter 1 / 19 | time 9[s] | perplexity 91.44
| epoch 42 |  iter 1 / 19 | time 10[s] | perplexity 87.73
| epoch 43 |  iter 1 / 19 | time 10[s] | perplexity 82.40
| epoch 44 |  iter 1 / 19 | time 10[s] | perplexity 79.73
| epoch 45 |  iter 1 / 19 | time 10[s] | perplexity 76.56
| epoch 46 |  iter 1 / 19 | time 10[s] | perplexity 72.09
| epoch 47 |  iter 1 / 19 | time 10[s] | perplexity 67.83
| epoch 48 |  iter 1 / 19 | time 10[s] | perplexity 66.07
| epoch 49 |  iter 1 / 19 | time 11[s] | perplexity 61.57
| epoch 50 |  iter 1 / 19 | time 11[s] | perplexity 59.53
| epoch 51 |  iter 1 / 19 | time 11[s] | perplexity 54.45
| epoch 52 |  iter 1 / 19 | time 11[s] | perplexity 52.73
| epoch 53 |  iter 1 / 19 | time 11[s] | perplexity 48.76
| epoch 54 |  iter 1 / 19 | time 11[s] | perplexity 47.42
| epoch 55 |  iter 1 / 19 | time 12[s] | perplexity 43.34
| epoch 56 |  iter 1 / 19 | time 12[s] | perplexity 41.73
| epoch 57 |  iter 1 / 19 | time 12[s] | perplexity 40.31
| epoch 58 |  iter 1 / 19 | time 12[s] | perplexity 37.41
| epoch 59 |  iter 1 / 19 | time 12[s] | perplexity 35.34
| epoch 60 |  iter 1 / 19 | time 13[s] | perplexity 32.87
| epoch 61 |  iter 1 / 19 | time 13[s] | perplexity 31.83
| epoch 62 |  iter 1 / 19 | time 13[s] | perplexity 29.90
| epoch 63 |  iter 1 / 19 | time 13[s] | perplexity 28.69
| epoch 64 |  iter 1 / 19 | time 13[s] | perplexity 26.16
| epoch 65 |  iter 1 / 19 | time 14[s] | perplexity 25.08
| epoch 66 |  iter 1 / 19 | time 14[s] | perplexity 24.05
| epoch 67 |  iter 1 / 19 | time 14[s] | perplexity 22.78
| epoch 68 |  iter 1 / 19 | time 14[s] | perplexity 21.47
| epoch 69 |  iter 1 / 19 | time 14[s] | perplexity 19.07
| epoch 70 |  iter 1 / 19 | time 14[s] | perplexity 18.68
| epoch 71 |  iter 1 / 19 | time 15[s] | perplexity 18.02
| epoch 72 |  iter 1 / 19 | time 15[s] | perplexity 16.84
| epoch 73 |  iter 1 / 19 | time 15[s] | perplexity 15.98
| epoch 74 |  iter 1 / 19 | time 15[s] | perplexity 14.68
| epoch 75 |  iter 1 / 19 | time 15[s] | perplexity 14.37
| epoch 76 |  iter 1 / 19 | time 15[s] | perplexity 13.93
| epoch 77 |  iter 1 / 19 | time 15[s] | perplexity 13.31
| epoch 78 |  iter 1 / 19 | time 16[s] | perplexity 12.49
| epoch 79 |  iter 1 / 19 | time 16[s] | perplexity 11.91
| epoch 80 |  iter 1 / 19 | time 16[s] | perplexity 11.18
| epoch 81 |  iter 1 / 19 | time 16[s] | perplexity 11.31
| epoch 82 |  iter 1 / 19 | time 16[s] | perplexity 10.22
| epoch 83 |  iter 1 / 19 | time 16[s] | perplexity 9.67
| epoch 84 |  iter 1 / 19 | time 16[s] | perplexity 9.06
| epoch 85 |  iter 1 / 19 | time 17[s] | perplexity 8.83
| epoch 86 |  iter 1 / 19 | time 17[s] | perplexity 8.56
| epoch 87 |  iter 1 / 19 | time 17[s] | perplexity 7.89
| epoch 88 |  iter 1 / 19 | time 17[s] | perplexity 7.37
| epoch 89 |  iter 1 / 19 | time 17[s] | perplexity 7.21
| epoch 90 |  iter 1 / 19 | time 17[s] | perplexity 7.24
| epoch 91 |  iter 1 / 19 | time 18[s] | perplexity 6.71
| epoch 92 |  iter 1 / 19 | time 18[s] | perplexity 6.51
| epoch 93 |  iter 1 / 19 | time 18[s] | perplexity 6.22
| epoch 94 |  iter 1 / 19 | time 18[s] | perplexity 5.98
| epoch 95 |  iter 1 / 19 | time 18[s] | perplexity 5.69
| epoch 96 |  iter 1 / 19 | time 18[s] | perplexity 5.48
| epoch 97 |  iter 1 / 19 | time 18[s] | perplexity 5.38
| epoch 98 |  iter 1 / 19 | time 19[s] | perplexity 4.93
| epoch 99 |  iter 1 / 19 | time 19[s] | perplexity 4.79
| epoch 100 |  iter 1 / 19 | time 19[s] | perplexity 4.53
"""