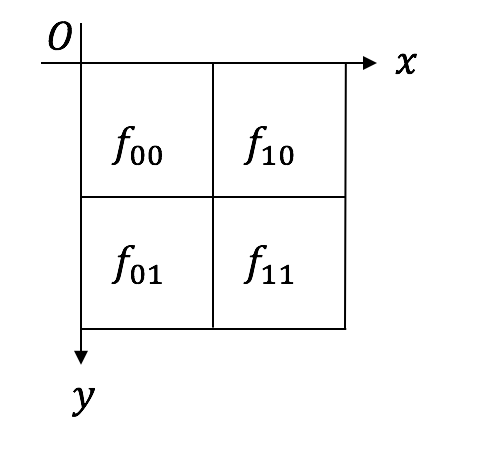はじめに
前回では、ハールウェーブレット(Haar Wavelet)による一次元の変換をしたので、今回は二次元の変換をやってみる。
一次元では、レベル$m$のスケーリング関数は、レベル$m-1$のスケーリング関数とウェーブレット関数に分解されるのだが、二次元以上の場合はスケーリング関数とウェーブレット関数の積に分解されるところがちょっとややこしい。
コードは
に置いてある。ウェーブレットを全く知らない人は先に一次元の記事を読んでおいた方が理解しやすいかも。
原理
ハールウェーブレットは、「平均」と「差分」に分解する。このうち「平均」を担当するのがスケーリング関数、「差分」を担当するのがウェーブレット関数である。一度分解すると、スケール半分の平均データと、その差分データとなる。さらにスケール半分の平均データを分解し・・・と再帰的に分解していくと、最終的に「全データの平均」一点と、様々なスケールの「差分」が残る。これが、データを最後まで分解すると一つのスケーリング関数と、多数のウェーブレット関数に分解される理由であった。二次元でも原理は同じである。
まず、以下のような$2 \times 2$の4点のモノクロ画像データを考える。後の画像データとの対応が良いように、y軸を下向きに取る。また、それぞれのピクセル値が$f_{00},f_{10},f_{01},f_{11}$であったとしよう。
それぞれのピクセルの場所に対応した、以下のような行列を考える1。
\begin{align}
D_{00} &=
\left(
\begin{matrix}
1 & 0 \\
0 & 0
\end{matrix}
\right) \\
D_{10} &=
\left(
\begin{matrix}
0 & 1 \\
0 & 0
\end{matrix}
\right) \\
D_{01} &=
\left(
\begin{matrix}
0 & 0 \\
1 & 0
\end{matrix}
\right) \\
D_{11} &=
\left(
\begin{matrix}
0 & 0 \\
0 & 1
\end{matrix}
\right)
\end{align}
明らかにこの4つの線形結合で先の$2\times 2$ピクセルの任意の値を表現できる。先の画像は
F =
\left(
\begin{matrix}
f_{00} & f_{10} \\
f_{01} & f_{01}
\end{matrix}
\right)
=
f_{00} D_{00} + f_{10} D_{10} + f_{01} D_{01} + f_{11} D_{11}
で表現される。また、これらは直交基底でもある。
これを、一次元の場合と同様に半分の解像度、つまり1ピクセルの値で置き換えたい。すると平均値を採用するのが良いだろう。それを左上に置くことにする。それ以外は、差分値を保存する。結果から書いてしまうと、以下の行列
\begin{align}
N_{00} &= \frac{1}{4}
\left(
\begin{matrix}
1 & 1 \\
1 & 1
\end{matrix}
\right) \\
N_{10} &=\frac{1}{4}
\left(
\begin{matrix}
1 & -1 \\
1 & -1
\end{matrix}
\right) \\
N_{01} &=\frac{1}{4}
\left(
\begin{matrix}
1 & 1 \\
-1 & -1
\end{matrix}
\right) \\
N_{11} &=\frac{1}{4}
\left(
\begin{matrix}
1 & -1 \\
-1 & 1
\end{matrix}
\right)
\end{align}
を使って
G =
\left(
\begin{matrix}
F:N_{00} & F:N_{10} \\
F:N_{01} & F:N_{11}
\end{matrix}
\right)
と変換する。ただし、$A:B$はフロベニウス積で、
A:B = \sum_{i,j} a_{ij} b_{ij}
である2。$G$の要素を明示すると、
G =
\frac{1}{4}
\left(
\begin{matrix}
f_{00}+f_{01}+f_{10}+f_{11} &
f_{00}-f_{01}+f_{10}-f_{11} \\
f_{00}+f_{01}-f_{10}-f_{11} &
f_{00}-f_{01}-f_{10}+f_{11}
\end{matrix}
\right)
となる。定義から明らかに左上の成分$F:N_{00}$が4つのピクセルの平均値であり、残りがそれぞれ、x方向の差分($F:N_{10}$)、y方向の差分($F:N_{01}$)、xy方向の差分($F:N_{11}$)であることがわかる。
この、$N_{00},N_{10},N_{01},N_{11}$が二次元のハールウェーブレット基底である。現在のレベル(解像度)を$m$とし3、ハールウェーブレットのレベル$m$のスケーリング関数を$\phi^{m}$、ウェーブレット関数を$\psi^{m}$とすると、
\begin{align}
N_{00} &= \phi^{m-1}(x)\phi^{m-1}(y)\\
N_{10} &= \psi^{m-1}(x)\phi^{m-1}(y)\\
N_{01} &= \phi^{m-1}(x)\psi^{m-1}(y)\\
N_{11} &= \psi^{m-1}(x)\psi^{m-1}(y)
\end{align}
と表現できる。このうち、スケーリング関数だけで書かれた$N_{00}$が、元画像を解像度半分(レベル$m-1$)で表現したものであり、それを再帰的に分解していくことで多重解像度解析は完了する。
実装
というわけで実装してみる。入力画像は、どこのご家庭にもあるであろうItanium2の写真である。入力画像は一辺が2のべきの正方形である必要がある。この例では512x512ピクセルとしている。あとで読み込むためにファイル形式はpngにしておこう。
ファイルの読み込みと配列への変換
まず、Cairo::ImageSurface::from_pngでファイルからサーフェスを作る。
require 'rubygems'
require 'cairo'
surface = Cairo::ImageSurface.from_png("itanium2.png")
あとはsurface.dataをいじれば良いが、これはStringオブジェクトになっており、そのままインデックス参照するとすこぶる遅い。なので一度unpackして配列にする。その後、アドレス下位から「G, B, R, 0」の成分に並んでいるので、その順番でRGBそれぞれのデータの値を得る。そのためのdata2rgbというメソッドを作ると便利。
def data2rgb(data)
buf = data.unpack("C*")
r = []
g = []
b = []
(buf.size/4).times do |i|
b.push buf[i*4+0]
g.push buf[i*4+1]
r.push buf[i*4+2]
end
return r,g,b
end
これで
r,g,b = data2rgb(surface.data)
とすればRGBデータがそれぞれ一次元の配列に入る。逆変換も作っておく。
def rgb2data(r,g,b)
s = r.size
buf = []
s.times do |i|
buf.push b[i]
buf.push g[i]
buf.push r[i]
buf.push 0
end
buf.pack("C*")
end
さらにファイルからの読み込み、書き込みメソッドも作っておこう。
def png2rgb(filename)
surface = Cairo::ImageSurface.from_png(filename)
abort("Image must be square.") if surface.height != surface.width
s = surface.height
abort("Image size must a power of two.") if s != 2**(s.bit_length-1)
r,g,b = data2rgb(surface.data)
return r,g,b,s
end
def rpg2png(r,g,b,s,filename)
buf2 = rgb2data(r,g,b)
format = Cairo::FORMAT_RGB24
surface = Cairo::ImageSurface.new(buf2,format, s, s, 4*s)
surface.write_to_png(filename)
end
読み込み時はサイズも返すようにしている。
順変換
まずは順変換。一次元の時と同様な変換をすればインプレイスで変換できるのだが、ここでは半分に縮小した画像を左上に寄せることにするため、一度配列をコピーしておく必要がある。あとは式をそのままスクリプトに落とすだけなので難しくないと思う。4
def transform(a_out, size, level)
a_in = Marshal.load(Marshal.dump(a_out))
s2 = size/(2**level)
s2.times do |y|
s2.times do |x|
d00 = a_in[x*2 + y*2 *size]
d10 = a_in[x*2 + 1 + y*2 *size]
d01 = a_in[x*2 + (y*2+1) *size]
d11 = a_in[x*2 + 1 + (y*2+1) *size]
n00 = (+ d00 + d10 + d01 + d11)/4.0
n10 = (+ d00 - d10 + d01 - d11)/4.0
n01 = (+ d00 + d10 - d01 - d11)/4.0
n11 = (+ d00 - d10 - d01 + d11)/4.0
a_out[x + y * size] = n00
a_out[x + s2 + y * size] = n10
a_out[x + (y+s2) * size] = n01
a_out[x+s2 + (y+s2) * size] = n11
end
end
end
これを、RGB成分それぞれについて呼んでやれば変換できる。
r,g,b,s = png2rgb("itanium2.png")
transform(r,s,1)
transform(g,s,1)
transform(b,s,1)
rpg2png(r,g,b,s,"output.png")
結果はこんな感じ。
元画像が、左上に半分に縮小された画像、右上にx方向の差分、左下にy方向の差分、右下にxy方向の差分と、4つの成分に分解された。
逆変換
逆変換も簡単にできる。
先の変換の
n00 = (+ d00 + d10 + d01 + d11)/4.0
n10 = (+ d00 - d10 + d01 - d11)/4.0
n01 = (+ d00 + d10 - d01 - d11)/4.0
n11 = (+ d00 - d10 - d01 + d11)/4.0
この部分は、ベクトルに4x4の行列をかけているとみなすことができる。具体的には
\left(
\begin{matrix}
n00 \\
n10 \\
n01 \\
n11
\end{matrix}
\right)
=
\frac{1}{4}
\left(
\begin{matrix}
1 & 1 & 1 & 1 \\
1 & -1 & 1 & -1 \\
1 & 1 & -1 & -1 \\
1 & -1 & -1 & 1
\end{matrix}
\right)
\left(
\begin{matrix}
d00 \\
d10 \\
d01 \\
d11
\end{matrix}
\right)
中央に出てくる行列は直交行列なので、逆行列は簡単に計算できて、
\left(
\begin{matrix}
d00 \\
d10 \\
d01 \\
d11
\end{matrix}
\right)
=
\left(
\begin{matrix}
1 & 1 & 1 & 1 \\
1 & -1 & 1 & -1 \\
1 & 1 & -1 & -1 \\
1 & -1 & -1 & 1
\end{matrix}
\right)
\left(
\begin{matrix}
n00 \\
n10 \\
n01 \\
n11
\end{matrix}
\right)
これをそのままスクリプトにすれば逆変換完成。
def inv_transform(a_out, size,level)
a_in = Marshal.load(Marshal.dump(a_out))
s2 = size/(2**level)
s2.times do |y|
s2.times do |x|
n00 = a_in[x + y * size]
n10 = a_in[x + s2 + y * size]
n01 = a_in[x + (y+s2) * size]
n11 = a_in[x+s2 + (y+s2) * size]
d00 = (+ n00 + n10 + n01 + n11)
d10 = (+ n00 - n10 + n01 - n11)
d01 = (+ n00 + n10 - n01 - n11)
d11 = (+ n00 - n10 - n01 + n11)
a_out[x*2 + y*2 *size] = d00
a_out[x*2 + 1 + y*2 *size] = d10
a_out[x*2 + (y*2+1) *size] = d01
a_out[x*2 + 1 + (y*2+1) *size] = d11
end
end
end
先程つくった output.pngを逆変換してみる。
r,g,b,s = png2rgb("output.png")
inv_transform(r,s,1)
inv_transform(g,s,1)
inv_transform(b,s,1)
rpg2png(r,g,b,s,"inversed.png")
実行結果。
元に戻った。
多重解像度解析
先程は一回だけ変換したが、元画像の一辺が$2^m$ピクセルある時、再帰的に$m$回変換すれば多重解像度解析の完成となる。
r,g,b,s = png2rgb("itanium2.png")
l = s.bit_length-1
l.times do |i|
transform(r,s,i+1)
transform(g,s,i+1)
transform(b,s,i+1)
end
rpg2png(r,g,b,s,"transformed.png")
l.times do |i|
inv_transform(r,s,9-i)
inv_transform(g,s,9-i)
inv_transform(b,s,9-i)
end
rpg2png(r,g,b,s,"restored.png")
実行結果。
- 元画像
itanium2.png
- 変換後
transformed.png
- 逆変換後
restored.png
正しく変換できているようだ。
まとめ
もっとも簡単なウェーブレットであるハールウェーブレットによる二次元画像の変換、逆変換を試してみた。ウェーブレットの説明でよくある「左上に半分になった元画像があり、残りになんかゴミっぽいものがある」画像について、それぞれ(ハールウェーブレットの場合には)
- 4つのピクセルの平均値
- x方向の差分
- y方向の差分
- xy方向の差分
であることがわかった。一次元の場合と同様、これは可逆変換なので、元に戻る。分解した後、係数の小さいウェーブレット基底を無視したりなんだりすることで圧縮するんだと思う(そのへんまだよく分かっていない)。
二次元ハールウェーブレット変換は、要するに
\left(
\begin{matrix}
1 & 0 \\
0 & 0
\end{matrix}
\right)
,
\left(
\begin{matrix}
0 & 1 \\
0 & 0
\end{matrix}
\right)
,
\left(
\begin{matrix}
0 & 0 \\
1 & 0
\end{matrix}
\right)
,
\left(
\begin{matrix}
0 & 0 \\
0 & 1
\end{matrix}
\right)
という4つの自明な基底から、
\left(
\begin{matrix}
1 & 1 \\
1 & 1
\end{matrix}
\right)
,
\left(
\begin{matrix}
1 & -1 \\
1 & -1
\end{matrix}
\right)
,
\left(
\begin{matrix}
1 & 1 \\
-1 & -1
\end{matrix}
\right)
,
\left(
\begin{matrix}
1 & -1 \\
-1 & 1
\end{matrix}
\right)
という基底への変換を繰り返すだけであると理解できる。特に、最初の全て要素が1の基底は、単純に4点を平均して一点にまとめる処理となっており、例の4分割された画像の左上に対応する。残りは平均からの差分を表現する。ハールウェーブレットの場合は基底の表現が簡単になるが、ドブシーウェーブレットの場合も、気持ちは同じなんだと思われる。
あと、速度を気にしないで組んだのでものすごく遅い。ちゃんと組めば相当高速化できると思うが、それならもっと高度なウェーブレットで変換したほうがいろいろ良いかもしれない。
あと、書いている本人はわかりやすく書いたつもりだったんだけど、読み返してみるとあまり直感的な記事になってないですね・・・。そのうち書き直すかも。