「九九の一の位」の数学的側面

はじめに

小学二年生の息子がこんな宿題を持ってきました。

今日息子が持って帰ってきた「円を十等分し、九九の一桁目の点をつなげ」という宿題、面白い。これ、10を法とする剰余類になっている。10と互いに素な奴はすべての点を巡る。また、1と9、2と8といった、「足して10になるペア」は同じ形になる。5は自己共役ですね。 pic.twitter.com/xOrF5I22jI

— ロボ太 (@kaityo256) 2018年11月22日

宿題の中身はこんな感じです。

円が10等分されており、0から9までの数字が書いてあります。この円で、九九の「一の位」を線で結んでみましょう。同じ形はあるかな？

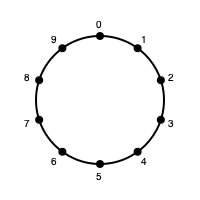
まず、10等分されて0から9までの数字が書いてある円というのがこんな感じです。

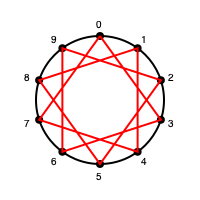
たとえば3の段なら、0からスタートして、3→6→9→2→5→8・・・と点を結んでいって、こんな図形になります。

こうして、1の段から9の段までの図を作るとこんな感じになります。

これを見ると

• すべての点を巡るものと巡らないものがある
• 2と8、3と7など、「足して10になるペア」は同じ形になる(線を結ぶのは逆向き)。
• 5は同じ形が存在せず、仲間はずれになっている

といったことがわかります。

これ、九九を学び始めた小学生の宿題としては定番のようで、去年も話題になったようですね。「数学ガール」にもこの話題があるそうなのですが、(全巻読んだはずなのですが)ちょっと覚えていません¹。

とりあえずこの「九九の一の位」から想起される数学的な話題について、つらつら書いてみようと思います。なお、筆者はちゃんとした数学徒ではないので、不正確な言葉遣いをすると思いますがどうかご容赦ください。

剰余類について

まず、「一の位」だけを考えることは、「10で割った余りを考えること」に他なりません。たとえば4、14、24はmod 10で同じになります。こうして「異なるものを、ある基準で同一視してできるグループ」を同値類といいます。同値関係を「~」で表現すると、同値類の公理は以下の3つです。

• 反射律: a ~ aは常に成り立つ
• 対称律: a ~ b なら b ~ aである
• 推移律: a ~ b かつ b ~ c なら a ~ cが成り立つ

同値類の初等的な例としては「図形の相似」があります。自分自身とは必ず相似で、aがbに相似ならbはaに相似で、aとbが相似、bとcが相似ならaとcも相似です。このように相似は同値類の公理を満たすので同値類を作ります。

さて、「何かで割った余り」も同値類を作ります。たとえば4と14はmod 10、つまり10で割った余りが同じになります。このように、mod 10をとって同じ数字になるグループを 10を法とする剰余類 と呼び、剰余類の中で代表的な元を 代表元 と呼びます。たとえば{4, 14, 24, 34, ..}が剰余類で、4がその代表元です。

さきほどの「円のまわりにある0から9の数字」は、10を法とする剰余類の代表元たちです。たとえば5の段なら、5→10→15→20→...となりますが、10で割った余りで考えると、0→5→0→5となります。これは、{5, 15, 25, ...}を同じものとみなし、その代表元が5、そして{10,20,30,...}を同じものとみなし、その代表元が0なので、5と0を交互に結ぶ、ということに対応します。

先のつぶやきで「10を法とする剰余類」と言ったのはそういう意味です。

巡回群

さて、先程の円の上の数字を線で結ぶ操作ですが、まるでダイヤルを回しているようです。そこで10目盛りあるダイヤルを回す操作を考えてみましょう。

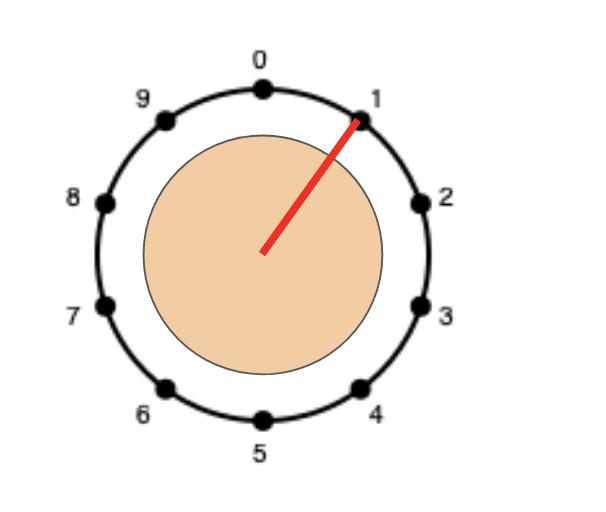
ここで、「右にn目盛り回す」という操作を$g_n$と書くことにします。ただし$0 \leq n<10$とします。最初に0を指していたダイアルを、右に$m$目盛りまわし、さらに右に$n$目盛り回すと、ダイアルは$m+n \mod 10$の位置にきます。これは0から9のどれかです。また、右に$n$目盛り回し、その後に右に$10-n$目盛り回すと、また0に戻ります。このように、「操作と、操作の対象があり、任意の操作を取り消すことができる」場合、この操作は群を作ります。

例えば、右に6目盛り回す操作$g_6$と、7目盛り回す操作$g_7$を続けて行うと、右に3目盛り回す操作$g_3$と等価です。つまり$g_6 \cdot g_7 = g_3$です。結合法則、単位元の存在、逆元の存在についてもすぐにわかるかと思います。

さて、10を法とする剰余類の代表元は0から9で、ダイアルの指す先はこのどれかです。
いま、ダイアルを0にしておいて、同じ操作だけを何回もかけることを考えましょう。例えば$g_3$だけをひたすらかけます。すると、ダイアルのさす先は0からスタートして、3→6→9→2→5→8となっていきます。これは「九九の3の段の一の位」に他なりません。これに対応して、$g_3^2 = g_6$、$g_3^3 = g_9$、$g_3^4 = g_2$・・・と次々と異なる操作が生まれます。このように、群の一つの元だけで生成される群を巡回群と呼びます。九九の任意の段の一の位は、自然に巡回群を定めます。

さて、$g_n$で生成される巡回群について、0から9すべてを巡る場合とそうでない場合があります。たとえば$g_5$を何回かけてもダイアルは0か5しか指しません。一方、$g_3$を何度もかける(右に3目盛り回す操作を繰り返す)と、ダイアルは0から9すべてを指します。すぐにわかるように、$g_n$だけをかけて全ての状態を取るためには、$n$が10と互いに素である場合に限られるのですが、これは$g_n^m$を$n \times m \mod 10$という積演算と見て、この演算において逆元が存在するかどうかに依存します。

ある元$a$の逆元$b$とは、$ab = 1$となるような元です。ただし$1$は乗法に関する単位元です。「普通の掛け算の世界」では、3に何かかけて1にするためには1/3を掛ける必要があり、世界を整数から有理数まで広げる必要があります。しかし、剰余類の世界、今回のケースではmod 10の世界では、整数の範囲内で逆元が存在できます。たとえば、$3\times7 = 1 \mod 10$なので、3と7は互いに逆元の関係にあります。9は9自身が逆元です。2は偶数ですから、何をかけても「10で割ってあまり1」にすることはできません。4,6,8も同様です。また、5は何回かけても一の位は0か5ですから、やはり逆元は存在しません。以上から、2,4,5,6,8が作る図形は点をすべて尽くしません。尽くすのは1,3,7,9の段で、それぞれ10と互いに素であることがわかるかと思います。

回転群

さて、「目盛りを回す」という操作から、自然に回転群を考えたくなりますね。ここでは、$g_n$という操作は、角度$\theta_n = 2n\pi/10$だけ回転する操作になります。その回転を表す行列は

\begin{pmatrix}
\cos \theta_n & -\sin \theta_n \\
\sin\theta_n  & \cos \theta_n 
\end{pmatrix}

となります。これは$g_n$の行列表現です。これを$A_n$と書くことにしましょう。さて、この行列の転置をとってみましょう。こうなります。

{}^t A=
\begin{pmatrix}
\cos \theta_n & \sin \theta_n \\
-\sin\theta_n  & \cos \theta_n 
\end{pmatrix}

さて、いま$\sin (2\pi - \theta_n) = -\sin \theta_n$でした。また、$\theta_n$の定義から、$2\pi - \theta_n = \theta_{10-n}$です。また、$\cos \theta_n = \cos \theta_{10-n}$もすぐにわかります。 以上から、

{}^t A_n=
\begin{pmatrix}
\cos \theta_{10-n} & -\sin \theta_{10-n} \\
\sin\theta_{10-n}  & \cos \theta_{10-n} 
\end{pmatrix}
= A_{10-n}

です。つまり、$g_n$の表現行列$A_n$の転置行列${}^t A_n$は$A_{10-n}$となります。これが「足して10となるペアが共役となる＝同じ形となる」理由です。また、$g_5$は対角行列となるため、転置をとっても自分自身になります。つまり、自己共役です。

まとめ

というわけで、「九九の一の位」から想起される数学のあれこれを綴ってみました。「一の位だけ考える」ことから剰余類が、「nの段が点を尽くすかどうか考える」ことから巡回群が、「同じ形になるペアについて考える」とから回転群が出てきました。たかが九九なのに、剰余類、巡回群、回転群、そしてその表現行列の性質・・・と様々な話題がでてきます。また、ここでは触れませんでしたが、10を法とする剰余類は方程式$x^{10} = 1$の根とみなすこともできます。回転が出てきたら、二次元回転は可換だが、三次元回転は非可換であることにも触れたくなります。暗号について語りたいひともいるでしょう。まだまだ話題はつきません。

この記事が小学二年生のお子さんのいる家庭の話題提供になれば幸いです。

Rubyスクリプト

ついでに、さきほどの図を作るRubyスクリプトもおいておきます。

kuku.rb

require "cairo"

$size = 200
$r = 64

def getxy(index, r)
  s = Math::PI * 2.0 / 10 * index - Math::PI * 0.5
  ix = r * Math::cos(s) + $size / 2
  iy = r * Math::sin(s) + $size / 2
  return ix, iy
end

def draw(n)
  surface = Cairo::ImageSurface.new(Cairo::FORMAT_RGB24, $size, $size)
  context = Cairo::Context.new(surface)
  context.set_source_rgb(1, 1, 1)
  context.rectangle(0, 0, $size, $size)
  context.fill

  context.set_source_rgb(0, 0, 0)
  context.circle($size / 2, $size / 2, $r)
  context.stroke

  10.times do |i|
    ix, iy = getxy(i,$r)
    context.move_to(ix,iy)
    context.circle(ix, iy, 4)
    context.fill
    ix, iy = getxy(i,$r+12)
    ix -= 4
    iy += 4
    context.move_to(ix,iy)
    context.show_text("#{i}")
    context.stroke
  end

  context.set_source_rgb(1, 0, 0)
  sx, sy = getxy(0,$r)
  context.move_to(sx, sy)
  (1..10).each do |i|
    sx, sy = getxy((i * n) % 10, $r)
    context.line_to(sx, sy)
  end
  context.stroke
  filename = sprintf("g%d.png", n)
  surface.write_to_png(filename)
end

(1..9).each do|n|
  draw(n)
end

実行するとg1.pngからg9.pngを作ります。

1. すみません＞結城先生。後で発掘して読み返します。 ↩