ドブシーウェーブレットを構成する

はじめに

JPEG2000にも採用されたウェーブレットによる多重解像度解析だが、その理解は難しい。難しさの理由はいろいろあろうが、個人的な印象としては「スケーリング関数、ウェーブレット関数をどうやって構成して良いかわからない」ということにあると思う。特に一番簡単なHaarウェーブレットはともかく、高次のドブシーウェーブレット(Daubechies Wavelets)はclosed formで書けないこともあって理解が難しい。教科書などを見ても高等な数式が多数でてきてよくわからない。

そこで本稿ではなるべく初等的な数学だけを使ってドブシーウェーブレットのN4を構成してみる。

ウェーブレットの性質

多重解像度解析には、二種類の関数が出現する。一つはスケーリング関数$\phi$、もう一つはウェーブレット関数$\psi$である。それらは、以下のtwo-scale関係式というものを満たす¹。

\begin{align}
\phi(x) &= \sum_{k=0}^{N-1} h_k \phi(2x - k) \\
\psi(x) &= \sum_{k=0}^{N-1} g_k \phi(2x - k) 
\end{align}

ただし、$h_k$と$g_k$は展開係数で、

g_k = (-1)^k h_{N-k-1}

を満たす。$N$は展開の次数である。

さて、上記に加えて、ウェーブレット関数とスケーリング関数の正規化条件を課す。

\begin{align}
\int \phi(x) dx &= 2 \\
\int \psi(x) dx &= 0
\end{align}

ドブシーウェーブレットでは、さらにいくつか重要な条件を課す。まず、スケーリング関数が空間的に局在しており、$0 \le x < N-1$でのみ0でない値を取るとする。さらに、「整数だけ距離が離れたスケーリング関数は直交する」ことを要請する。つまり、普通の関数の内積、

\langle f,g \rangle \equiv \int f(x) g(x) dx

を用いて、直交条件

\langle\phi(x), \phi(x-n) \rangle = 2 \delta_{n,0}

を満たすとする(ただし$n$は整数)²。

これによりスケーリング関数、ウェーブレット関数を構成することができる。

Haarウェーブレットの場合

係数の決定

$N=2$の場合、最も簡単なHaarウェーブレットになる。この時、two-scale関係式は

\phi(x) = h_0 \phi(2x) + h_1 \phi(2x-1)

で表現される。ここから係数$h_0$と$h_1$を決めてみよう。

まず、直交条件で$n=0$を代入すると、

\langle \phi(x) \phi(x) \rangle = 2

となる。ここでtwo-scale関係式を使って$\phi(x)$を$\phi(2x)$と$\phi(2x-1)$を使ってバラすのだが、直交条件から「同じ関数」が出てきたところしか値が残らない。ここから、

h_0^2+ h_1^2 = 2

を得る。さらに、$\phi$と$\psi$の正規化条件により、

\begin{align}
h_0 + h_1 &= 2 \\
h_0 - h_1 &= 0
\end{align}

を得る。ここから容易に$h_0=1, h_1 =1$が得られる。

スケーリング関数の構成

さて、係数から$\phi(x)$を構成する。two-scale関係式に$x=1/2$を代入してみよう。

\phi(1/2) = \phi(0) + \phi(1)

ここで$\phi(0)$と$\phi(1)$の値が必要になるが、局在性の定義より$\phi(1)=0$である。$\phi(0)$の値はなんでも良い。とりあえず適当に$\phi(0) = 1$と決めて、後で正規化条件で調整しよう。すると$\phi(1/2)=1$となる。

次に$x=1/4$を代入してみる。two-scale関係式から

\phi(1/4) = \phi(1/2) + \phi(-1/2)

となる。局在性の条件から$\phi(-1/2)=0$であるので、$\phi(1/4) = 1$である。同様に$x=3/4$を代入すると、

\phi(3/4) = \phi(3/2) + \phi(1/2)

となる。ここでも$\phi(3/2)=0$であるから、やはり$\phi(3/4)=1$である。

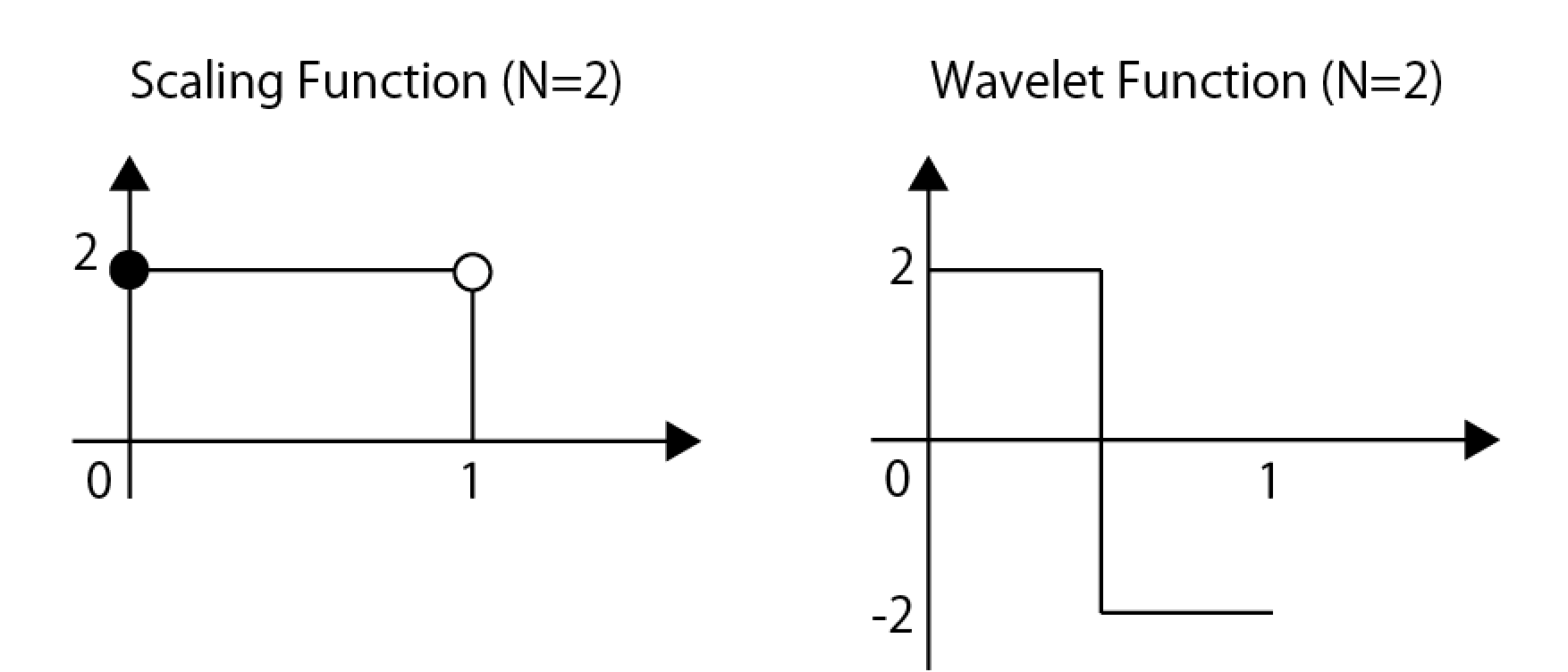
以上のように、次々と格子点を半分にしていくと、$0 \le x < 1$において$\phi(x) = 1$、それ以外はゼロであることがわかる。最後に、正規化条件を満たすように全体を定数倍すると$\phi(x) = 2$となる。

スケーリング関数$\phi$がわかると、two-scale関係式からウェーブレット関数$\psi$も決めることができる。図示するとこんな感じ。

ドブシーウェーブレット(N=4)

さて、$N=2$の場合は簡単だったが、次に簡単な$N=4$のケースは急に面倒になる。
同様にtwo-scale関係式を書き下すと、

\phi(x) = h_0 \phi(2x) + h_1 \phi(2x-1) + h_2 \phi(2x-2) + h_0 \phi(2x-3)

となる。スケーリング関数とウェーブレット関数の正規化条件から直ちに

\begin{align}
h_0 + h_1 + h_2 + h_3 &= 2 \\
h_0 - h_1 + h_2 - h_3 &= 0 \\
\end{align}

がわかる。次に、直交条件に$n=0$を代入すると、

h_0^2+h_1^2+h_2^2 +h_3^2 = 2

となる。$N=2$の場合は直交条件は$n=0$しか意味のある情報を与えなかったが、$N=4$の場合は$n=1$の場合から以下の条件が出てくる。

h_0 h_2 + h_1 h_3 = 0

以上をまとめると、

\begin{align}
h_0^2+h_1^2+h_2^2 +h_3^2 &= 2 \\
h_0 + h_1 + h_2 + h_3 &= 2 \\
h_0 - h_1 + h_2 - h_3 &= 0 \\
h_0 h_2 + h_1 h_3 &= 0
\end{align}

を得るが、これらは独立ではなく、これだけでは値が決まらない。とりあえず2番目と3番目の式を足すと

h_0 + h_2 = 1

であることがわかる。ここからすぐに

h_1 + h_3 = 1

もわかる。しかし、これ以上は値が決まらないので、適当に一つ条件

h_0 + h_3 = 1/2

を付け加える³。これにより全て値が決まる。まず、ただちに

h_1 + h_2 = 3/2

がわかる。ここから$h_1,h_2,h_3$を全て$h_0$で表現できるので、自乗和の式に代入して整理すると、

4 h_0^2 - 2 h_0 - 1/2 = 0

これは容易に解けて、

h_0 = \frac{1 \pm \sqrt{3}}{4}

複号はどちらでも良いが、正の方を取ろう。すると、

\begin{align}
h_0 &= \frac{1 + \sqrt{3}}{4} \\
h_1 &= \frac{3 + \sqrt{3}}{4} \\
h_2 &= \frac{3 - \sqrt{3}}{4} \\
h_3 &= \frac{1 - \sqrt{3}}{4} \\
\end{align}

と求まる。

スケーリング関数の整数点の構成

two-scaling関係式に、$x=0,3$を代入してみよう。局在条件$\phi(x) = 0 (x<0, x \ge N-1)$に注意すると、

\begin{align}
\phi(0) &= h_0 \phi(0) \\
\phi(3) &= h_3 \phi(3) 
\end{align}

ここから直ちに$\phi(0) = 0, \phi(3) = 0$がわかる。次に、$x=1, 2$を代入してみる。

\begin{align}
\phi(1) &=  h_1 \phi(1) + h_0 \phi(2) \\
\phi(2) &=  h_3 \phi(1) + h_2 \phi(2)
\end{align}

である。これは固有値問題となっており、固有値1のベクトルを探せば良い。
$\phi(1) = 1$、$\phi(2) = y$とすると、

\begin{align}
1 &=  h_1 + h_0 y \\
y &=  h_3 + h_2 y
\end{align}

これはどちらも同じ解、

y = \phi(2) = \frac{1-\sqrt{3}}{1+\sqrt{3}}

を与える。

以上から、$N=4$の場合のドブシーウェーブレットのスケーリング関数$\phi(x)$の整数点$x=0,1,2,3$の値が全てもとまった。

ドブシーウェーブレット(N=2)の構成

整数点がわかってしまえば、Haarウェーブレットの場合と同様にtwo-scaling関係式を使って次々と格子点の値を求めていくことができる。

例えば、$x=1/2$の場合なら、

\phi(1/2) = h_0 \phi(1) + h_1 \phi(0)

$x=3/2$なら、

\phi(3/2) = h_0 \phi(3) + h_1 \phi(2) + h_2 \phi(1) + h_3 \phi(0)

であり、既知の値から求めることができる。このようにして、$n/2^m$の点($n$は整数)が求められたら、それらを使って$n/2^{m+1}$の点の値を求めることができる。

以上の手続きのプログラムにするとこんな感じになるだろう。

daubecies.rb

$M = 8
$N = 4+3*(2**$M-1)
data = Array.new($N){0}

data[2**$M] = 1.0 # \phi(1) = 1.0
data[2**$M*2] = (1-Math::sqrt(3))/(1+Math::sqrt(3)) # \phi(2) = (1-sqrt(3))/(1+sqrt(3))

$h = [0.683012,1.1830127,0.3169873,-0.1830127]
$g = [-$h[3],$h[2],-$h[1],$h[0]]

def phi(t,data)
  sum = 0.0
  4.times do |i|
    t2 = 2*t - 2**$M*i
    next if t2 < 0
    next if t2 >= $N
    sum = sum + $h[i]*data[t2]
  end
  sum
end

def psi(t,data)
  sum = 0.0
  4.times do |i|
    t2 = 2*t - 2**$M*i
    next if t2 < 0
    next if t2 >= $N
    sum = sum + $g[i]*data[t2]
  end
  sum
end

$M.times do |i|
  (3*(2**i)).times do |j|
    x =  2**($M-i-1) + (2**($M-i))*j
    data[x] = phi(x,data)
  end
end

sum = data.inject{|sum,v| sum+v}
s = $N/3.0/sum*2.0
data.map!{|v| v*s} # 正規化

$N.times do |i|
  puts "#{i.to_f/$N*3} #{data[i]} #{psi(i,data)}"
end

簡単なので解説は不要だと思われるが、手抜きスクリプトなので補足しておくと、

• 求める解像度レベルは$M
• スケーリング関数は配列dataに入る
• 最後に正規化条件でデータをリスケールしている。
• ウェーブレット関数は、スケーリング関数が求まったらtwo-scale関係式で求めている(関数psi)

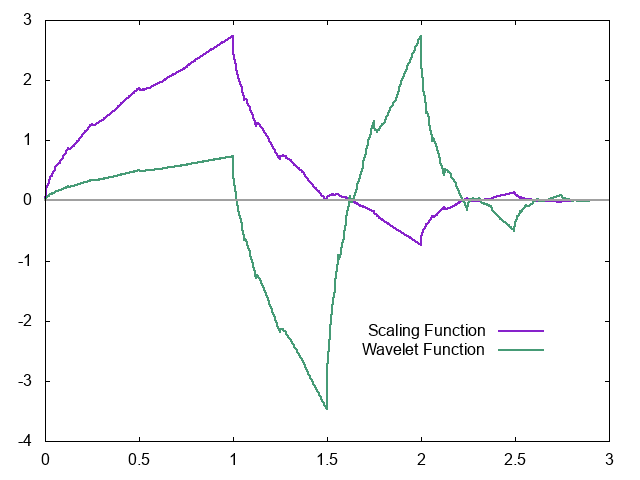
という感じ。結果はこうなる。

無事にそれっぽい図がでてきた。Wikipediaの図と二倍ずれているのは、正規化条件が2倍異なるからである。

まとめ

$N=4$の場合において、ドブシーウェーブレットを構成してみた。ドブシーウェーブレットは$N=2$の場合はHaarウェーブレットとなり、それが単純なステップ関数になるのに比べて、$N>2$の場合は急に面倒になる。とりあえずウェーブレット関数やスケーリング関数の初等的な描き方が見つからなかったのでこの記事を書いてみたが、ウェーブレットを本格的に勉強する場合は参考文献を参照されたい。

参考

• ウェーブレット10講 ドブシーウェーブレットの生みの親、Ingrid Daubechiesによる講義資料。定番らしいのだが、筆者はちゃんと読んでない。

1. 各係数の前に$\sqrt{2}$をつける流儀もある。たぶんフーリエ変換で$\sqrt{\pi}$をつけるとかつけないとか言うのと同じなんだと思う。 ↩

2. ここでは正規化条件として係数$2$を与えたが、$1$にする流儀もあるので注意。Wikipediaなどは$1$を採用している。 ↩

3. なぜこうすべきかは筆者もよくわかっていない。興味ある人は教科書などを読んで下さい。 ↩