ナンプレの正規化 ステップ・バイ・ステップ その２

はじめに

Step1では、最低限の枝刈りだけを導入した。しかしRuby版は一問正規化するのに2秒近くかかっていて、さすがに遅いので、まずはRuby版にもう少しちゃんとした枝刈りを導入することにしよう。正規化の意味は独自用語については前回の記事参照のこと。

ソースコードは以下に置いてある。
https://github.com/kaityo256/minlex

方針

前回はヘッドボックスが完成するまで全く枝刈りをしなかった。しかし、それ以前にもっと枝刈りができる。ナンプレは81桁の数字の数字で表すことが可能で、その数字を最も小さいパターンを探すのが正規化であった。そこでまず、「どの行が一番上に来る可能性があるか」を考える。

ボックス行の入れ替えの枝刈り

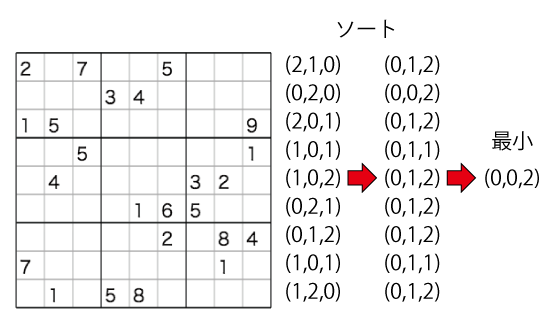
以下の図を見てみる。

各行に着目する。ボックス行ごとに入れ替えが可能なので、各行を3つずつにわけ、それぞれに何個ヒントがあるかを考えよう。一番上の行に着目するなら(2,1,0)となる。さて、もしこの行が一番上に来るならば、正規化された場合、ヒントは最も「右に寄る」はずなので(0,1,2)のパターンになるはずである。

同様に、二行目に着目すると、二行目が一番上に来た場合、正規化パターンのヒント配置は(0,0,2)になるはずである。ここで、ヒントの配置パターンが(0,1,2)の場合と(0,0,2)の場合は、どんな数字の振り方をしても(0,0,2)の方が値が小さくなる。従って、この瞬間、一番上の行が一番上に来ることは無い、ということがわかる。

さて、これを9行全てについて行うと、最小のヒントパターンは(0,0,2)であることがわかった。ここで、(0,0,2)のヒントパターンを含まないボックス行が一番上に来ることは無い。この例では、ボックス行の入れ替え6パターンのうち、一番上のボックス行が一番上にくることが確定したため、調べるべきパターンが2パターンになった。

もちろん、転置も考慮しなければならない。そこで、転置前、転置後のそれぞれについて、どのボックス行が一番上に来る可能性があるかを、6パターン調べ、最小のヒントパターンを調べておく。その後、そのヒントパターンを持つボックス行以外については再帰しないことで枝刈りをする。

ボックス列の入れ替え

さて、一番上のボックス行が確定したとする。次はボックス列の並べ替えである。先の例であれば、一番上のボックス行がそのまま一番上に居座るのが最小パターンであった。この時、一番上にくる行のヒントパターンは(0,2,0)である。この数字がなるべく右に寄るようにボックス列を入れ替えなければならない。そのパターンは既に(0,0,2)であることを知っているから、それ以外のパターンについては再帰しないで枝刈りができる。

ヘッドボックス行内の行の入れ替え

ボックス単位の入れ替えが終了したら、次はヘッドボックス内の行の入れ替えである。ヘッドボックスの行ごとのヒント数は(2,1,0)、(0,2,0)、(2,0,1)であるから、この時点で2行目が一番上にくることが確定する。ただし、同じヒントパターンを持つ行が複数ある場合もあるから、とりあえず6パターン全部尽くして、最小ヒントパターンと一致する場合のみ次に再帰することにする。

実装

さらに枝刈りは可能だが、一度ここで実装しておこう。

ボックス行の入れ替えの枝刈り

まず最初の枝刈りで必要なのは、ナンプレパターンを与えられた時、そのヘッドボックスの最小ヒントパターンを返すメソッドである。データは配列になっているので、まず最初の27個を9個ずつにスライスして、さらにそれを3個ずつにスライスして、ヒント数の配列にして、さらにそれをソートして返せば良い。こんな感じになるだろう。

def headbox_sorted_index(s)
  sh = s[0..26].each_slice(9).to_a
  sh.map do |shi|
    sa = shi.each_slice(3).to_a
    a2 = sa.map do |ai|
      ai.inject(0) {|sum,v| v!=0 ? sum + 1: sum}
    end.sort
    a2
  end.min
end

これを使って、まず可能な12パターン全部について、このヘッドボックスのインデックスを調べ、最小値hb_minを探すことにする。そして、最小値を持つヘッドボックスを持つパターン以外は弾くことで枝刈りをする。

def search(s)
  a = []
  sa = s.each_slice(27).to_a
  [0,1,2].permutation do |ai|
    a.push sa[ai[0]] + sa[ai[1]] + sa[ai[2]]
  end
  sa = transpose(s).each_slice(27).to_a
  [0,1,2].permutation do |ai|
    a.push sa[ai[0]] + sa[ai[1]] + sa[ai[2]]
  end
  hb_min = a.map{|v| headbox_sorted_index(v)}.min
  a.each do |si|
    next if headbox_sorted_index(si) > hb_min
    perm_cbox(si,hb_min)
  end
end

あとで使うために、最小パターンhb_minを引数として渡している。

ボックス列の入れ替えの枝刈り

次はボックス列の入れ替えに関する枝刈りである。先程はヒントパターンを(0,2,0)から(0,0,2)にソートしたものをインデックスとしたが、今度はソートしないものをインデックスとして、それが先程求めた最小ヒントパターン(0,0,2)に一致するものだけを通し、それ以外は弾く。

というわけで今度はソートしないインデックスを返すメソッドを作る。

def headbox_index(s)
  sh = s[0..26].each_slice(9).to_a
  sh.map do |shi|
    sa = shi.each_slice(3).to_a
    a2 = sa.map do |ai|
      ai.inject(0) {|sum,v| v!=0 ? sum + 1: sum}
    end
    a2
  end.min
end

これ書いた後で、「あ、ソートするかどうかを引数に渡せばよかった」と気がついたが、面倒なのでそのままにする(後で紹介するC++版にはそれを実装してある)。

これを使って、渡されてきた最小パターンhb_minと一致するパターンだけ通せば良い。

def perm_cbox(s,hb_min)
  st = transpose(s)
  sa = st.each_slice(27).to_a
  [0,1,2].permutation do |ai|
    si = sa[ai[0]] + sa[ai[1]] + sa[ai[2]]
    si = transpose(si)
    next if headbox_index(si) > hb_min
    perm_toprbox(si,hb_min)
  end
end

次でも使うので、やはりhb_minを引数に渡している。

ヘッドボックス内の行の入れ替え

さて、ボックス行、列の入れ替えが終了したので、次はヘッドボックス内の行の入れ替えを行う。もう(0,0,2)のヒントパターンを持つ行を一番上に持ってくれば良いことがわかっているので、それだけ通せば良い。具体的には、まず「一番上の行のヒントパターン」を返す関数headline_indexを用意する。

def headbox_index(s)
  sh = s[0..26].each_slice(9).to_a
  sh.map do |shi|
    sa = shi.each_slice(3).to_a
    a2 = sa.map do |ai|
      ai.inject(0) {|sum,v| v!=0 ? sum + 1: sum}
    end
    a2
  end.min
end

なんかさっきから似たようなメソッドばっかり書いて、もっと美しい方法がきっとあるんだろうなと思いつつ、気にしないで先に進む。

この一番上のヒントパターンを返す関数を使って、以下のように枝刈りができる。

def perm_toprbox(s,hb_min)
  sh,sm,sb = s.each_slice(27).to_a
  sa = sh.each_slice(9).to_a
  [0,1,2].permutation do |ai|
    si = sa[ai[0]] + sa[ai[1]] + sa[ai[2]]
    si = si + sm + sb
    next if headline_index(si) > hb_min
    perm_columns(si)
  end
end

まぁ、最小ヒントパターンに合致する行が一番上に来た時だけ通しますよ、という感じ。

結果

ここまで実装した結果で、またベンチマークをとってみる。

$ time ruby array.rb
207005000000340000150000009005000001040000320000016500000002084700000010010580000
000000012000034005006007300001300007053080000080000100010005090200100000700400030
OK
ruby array.rb  0.11s user 0.01s system 94% cpu 0.132 total

おおー、枝刈りを追加する前が1.71秒だったので、10倍ちょっと早くなった。

まとめ

Step 1では「上位27桁」にのみ着目して枝刈りをしたが、「上位9桁」に着目して枝刈りをすることで、わりとバサッと枝が刈れて早くなった。同様に「上位18桁」に着目して枝刈りできるか・・・と思うと、実は一番の行とからむのでわりと面倒くさい。興味のある人は考えて見られたい(っていうか多分もっと良い枝刈りポイントがある)。

その3へ続く。