線形代数を学ぶ理由

はじめに

少し前(2019年4月頃)に、「AI人材」という言葉がニュースを賑わせていました。「現在流行っているディープラーニングその他を使いこなせる人材」くらいの意味だと思いますが、こういうバズワードの例の漏れず、人によって意味が異なるようです。併せて「AI人材のために線形代数の教育をどうするか」ということも話題になっています。

線形代数という学問は、本来は極めて広く、かつ強力な分野ですが、とりあえずは「行列とベクトルの性質を調べる学問」と思っておけば良いです。理工系の大学生は、まず基礎解析とともに線形代数を学ぶと思います。そして、何に使うのかわからないまま「固有値」や「行列式」などの概念が出てきて、例えば試験で3行3列の行列の固有値、固有ベクトルを求め、4行4列の行列の行列式を求めたりしてイヤになって、そのまま身につかずに卒業してしまい、後で必要になって後悔する人が出てきたりします(例えば私)。

線形代数は重要な学問ですから、それを学ぶこと、強化すること自体は喜ぶべきことです。しかし、若い人がニュースなどを見て「線形代数はAIに必要だから重要」とか思ってしまうのは困ります。それでは「僕はAIをやるつもりないから線形代数いらない」という人が出てきてしまいます。

言うまでもありませんが、線形代数はAIに必要だから重要なのではありません。そもそも重要とか必要とかいうレベルではなく、誤解を恐れずにいえば「線形代数は理工系の学問のほぼ全ての領域にわたって必須」と言ってよい学問です。線形代数が関わる分野は膨大で、その全てをサーベイすることは私には不可能です。とりあえず本稿では、主に数値計算において「なぜ線形代数が重要であるか」を紹介したいと思います。

本稿は、大学の一年生ないし二年生で、線形代数を学んでいる or 学んだけど、何に使うかわからないので学ぶモチベーションがぼんやりしている、という学生さんを対象に書きます。以下、(特に用語の使い方において)かなりいい加減な書き方をするので、「線形代数が重要なのは当然だろ」と思っている人とか、数学ガチ勢な皆さんとかはブラウザの「戻る」ボタンを押してください。

用語の整理

まず、ざっと線形代数の用語の定義をしておきましょう。以下のような2行2列の行列を考えます。

A =
\begin{pmatrix}
5/4 & 3/4 \\
3/4 & 5/4
\end{pmatrix}

固有値と固有ベクトル

$$
A v = \lambda v
$$

のように、ある行列$A$にベクトル$v$をかけた結果$A v$が、入力ベクトルの定数倍$\lambda v$になった時、$v$を$A$の固有ベクトル、$\lambda$を固有値と呼ぶのでした。

先程の行列の固有ベクトルはそれぞれこんな感じになります。

v_1 =
\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\
1
\end{pmatrix}

v_2 =
\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\
-1
\end{pmatrix}

固有値はそれぞれ2と1/2です。

\begin{align}
A v_1 &= 2 v_1 \\
A v_2 &= \frac{1}{2} v_2
\end{align}

二つのベクトル$x,y$から一つのスカラー値を作る写像$(x,y)$を内積と呼びます¹。内積は、「あるベクトル$x$からあるベクトル$y$へ射影したときの長さ」、すなわち「あるベクトル$x$に、あるベクトル$y$の成分がどれくらい含まれるか」を表現するものです。内積が0の場合は、「このベクトル$x$はベクトル$y$の成分を全く含まない」ことを意味します。これを直交しているといいます。先程の二つの固有ベクトルはお互いに直交しています。直交しているからには平行ではありえません。お互いに平行ではないベクトルは線形独立であるといいます(直交性は必ずしも線形独立性の条件ではありません)。空間次元と同じ数だけ線形独立なベクトルの集合を持ってくれば、空間の任意のベクトルをそのベクトルの線形和で表現できるのでした。このようなベクトルを空間の基底と呼びます。

基底が、「自分自身との内積は1、それ以外の基底との内積が0」を満たす場合、その基底の集合を正規直交基底と呼びます。

基底の線形和で任意のベクトルを表現できるのでした。例えば、あるベクトル$a$を先程の基底で表現してみましょう。

a = c_1 v_1 + c_2 v_2

基底$v_1, v_2$が正規直交基底である場合、両辺$v_1$や$v_2$との内積を取るだけで、係数$c_1$や$c_2$が求まるのでした。

\begin{align}
(v_1,a) &= c_1 (v_1,v_1) + c_2 (v_1 , v_2)\\
&= c_1
\end{align}

ここで、$(v_1 , v_1 )= 1$、$(v_1 , v_2) = 0$を使っています。

この行列や固有値の意味を考えてみましょう。この行列$A$は、$v_1$の方向に2倍に引き伸ばし、$v_2$の方向に半分に縮めるような変換になっています。

この図を見ると、「時計回りに45度傾けたような座標で考えた方が楽そうだな」と気づくと思います。従って、例えば何かのベクトルに$A$を何度もかける必要がある場合、一度世界を回して固有ベクトルの張る空間にして、そのあと演算してから、また元に戻した方が計算が楽です。

行列式

行列$A$は、「ある方向に2倍に引き伸ばし、その方向と直交する方向に半分に縮める」という変換を引き起こすことから「$A$をかけるという変換が図形の形を変えても、面積は変えないだろう」という予想がつきます。実際に計算してみましょう。

ベクトル${}^t(1,0)$と${}^t(0,1)$とで表現された単位正方形が、行列$A$でどのような図形に移されるか見てみましょう。それぞれ$A$をかけると、${}^t(5/4,3/4)$と${}^t(3/4,5/4)$になります。二つのベクトル${}^t(a_1,a_2)$と${}^t(b_1,b_2)$で張られる四角形の面積は$|a_1 b_2 - b_1 a_2|$で計算されるのでした。これは行列$A$の行列式$|A|$にほかなりません。実際に計算してみると、$A$の行列式は1になります。

$$
|A| = \frac{5}{4} \times \frac{5}{4}

• \frac{3}{4} \times \frac{3}{4} = 1
  $$

これは、$A$による変換により、図形の面積が変化しないことを意味しています。

フーリエ・ラプラス解析

物理とは世の中を記述する学問ですが、世の中は「支配方程式」と呼ばれる微分方程式で記述されています。したがって、何か世の中を記述、理解したいと思えば、微分方程式を解く必要が出てきます。しかし、微分方程式は、一般に線形でなければ解くことができません。この線形(偏)微分方程式をフーリエ変換、もしくはラプラス変換で解けるようになる、というのが理工系の大学における数学の一つのハイライトとなります。「微分・積分」は「解析学」に属す概念でありながら、フーリエ変換やラプラス変換は線形代数における基底の変換になっている、と理解することがポイントです。

先程、二つのベクトルからスカラーを作る写像として内積を定義しました。同様に二つの関数$f, g$の間にも、以下のようにして内積が定義できます。

$$
(f,g) \equiv \int_{-\infty}^{\infty} f^* g dx
$$

ここで$f^*$は$f$の複素共役ですが、とりあえずは気にしなくて大丈夫です。フーリエ変換では、$\exp{(ikx)}$という「基底」で関数を展開するのでした。ある関数$f(x)$のフーリエ変換$\hat{f}(k)$を求めるのに、関数$f$と$\exp{(ikx)}$との内積、

\begin{align}
\hat{f}(k) &= (f, \exp{(ikx)}) \\
&= \int_{-\infty}^{\infty} f^* \mathrm{e}^{ikx} dx
\end{align}

を計算しているのを思い出しましょう。これは、$f(x)$という関数を様々な波数$k$を持つ基底関数で展開した時の、ある特定の$k$を持つ基底関数$\exp{(ikx)}$の係数を計算したことになります。つまりこれは、ある空間から$\exp{(ikx)}$という形の基底関数が張る空間への変換になっています。

ではなぜ$\exp{(ikx)}$という基底で展開するのでしょうか。それは指数関数が微分演算子の固有関数だからです。$\exp{(ikx)}$を$x$で微分しても$ik$が出てくるだけで、またもとの関数に戻ります。微分演算子を$A$、関数$\exp{(ikx)}$を$v_{ik}$と表現すると、

$$
A v_{ik} = ik v_{ik}
$$

となり、先程の2行2列の行列の場合と全く同様に扱えることがわかるでしょう。ラプラス変換も同様です。

このように、線形(偏)微分方程式がフーリエ・ラプラス変換で簡単に解けるのは、「指数関数が微分演算子の固有関数である」「固有関数で展開してしまえば計算が楽になる」という事実を利用しています。さらにいえば、これが「平面波展開」になっていることを授業で学ぶはずです。

ここで、演算子がもっとややこしい形をしていても、固有関数で展開してしまえば計算が楽になるだろう、と予想がつくでしょう。極座標の計算はかなり面倒ですが、球面調和関数を使えば計算が楽になります。これは球面調和関数が極座標のラプラシアンの固有関数になっているからです。エルミート多項式やルジャンドル多項式もまったく同様に理解できます。

数値計算

線形代数は様々な分野に顔を出しますが、数値計算でも極めて重要な役割を果たします。既に述べたように、この世界は微分方程式で記述されており、ほとんどの場合において厳密に解くことができません。そこで、数値的に近似解を求めることになりますが、その際に方程式を離散化することで数値的に扱えるようにします。すると、微分方程式という連続な世界から、自然に行列やベクトルが出てきます。スパコンのランキングで有名なTop500では、非常に大きな連立一次方程式を解きます。これは、ベンチマークとしてよい性質を持っている、ということもありますが、そもそも数値計算において馬鹿でかい連立一次方程式を解くというニーズがあるからベンチマークとして選ばれているという側面もあります。以下では、微分方程式を離散化すると、線形代数が顔を出す様子を見てみましょう。

熱伝導方程式

まず、簡単な例として熱伝導方程式を考えましょう。一次元ならこんな方程式です。

$$
\frac{\partial T}{\partial t} = \frac{\partial^2 T}{\partial x^2}
$$

ここで、$T(x;t)$は、時刻$t$における位置$x$の温度です。周期境界条件をとるので、輪になっている針金の温度を表現していると思ってください。簡単のため、熱伝導率を1としています。さて、この方程式はフーリエ変換で厳密に解けますが、差分化して数値的に解くことにします。空間方向は刻み幅1で、時間方向は時間刻み$h$で離散化しましょう。$t=0$を$0$ステップ目とすると、$n$ステップ目、$i$番目の位置の温度を$v_n^i$で表現します。先ほどの微分方程式を、空間方向は中央差分、時間方向は一次のオイラー法で差分化すると、

$$
v^i_{n+1} = v^i_n + h (v_n^{i-1} - 2 v_n^i + v_n^{i+1})
$$

と書き換えられます。初期条件として$v_0^i$が与えられれば、上記の式に従って$v_1^i, v_2^i, \cdots ,v_n^i$と、任意の時刻、場所の温度が求められることになります。これを素直にコードに実装してみましょう。空間を$N$分割し、周期境界条件を課して、初期条件として山型の温度分布を与えます。適当な時間刻みで時間発展させ、途中の温度を重ねてプロットするPythonコードはこんな感じになるでしょう²。

import copy
import matplotlib
import matplotlib.pyplot as plt
import numpy as np

def calc(v, h):
    v2 = copy.copy(v)
    N = len(v)
    for i in range(N):
        i1 = (i+1) % N
        i2 = (i - 1 + N) % N
        v[i] = v2[i] + (v2[i1] - 2.0*v2[i] + v2[i2])*h

N = 32
v = np.array([min(x, N-x) for x in range(N)], dtype='float64')

h = 0.1
r = []
for i in range(1000):
    calc(v, h)
    if (i % 100) == 0:
        r.append(copy.copy(v))

for s in r:
    plt.plot(s)

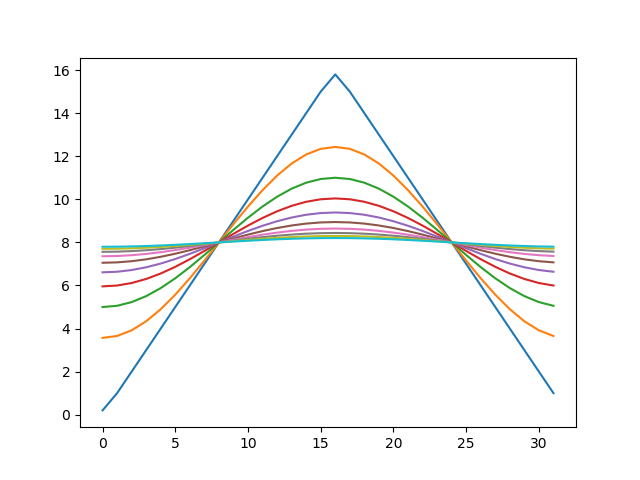
上記をJupyter NotebookかGoogle Colabで実行すれば、以下のような出力が得られます。

初期条件として山型の温度分布を与えたのが、だんだんとなまっていき、最終的に直線、すなわち一様な温度分布になったことがわかります。

さて、先ほどの離散化した式ですが、以下のような行列とベクトルの積の成分を表示したものと思うことができます。

\vec{v}_{n+1} = A \vec{v}_n

ただし、$A$は以下のような形をした$N$行$N$列の行列です。

対角成分が$1-2h$、その両隣が$h$となる三重対角行列になっていますが、周期境界条件の影響で、上端と下端だけ$h$の場所がずれています。

もともと時間発展は微分方程式で記述されていましたが、離散化により状態がベクトルで表現され、そのベクトルに行列をかけると次のステップの状態が得られる、という行列とベクトルの問題に帰着されました。離散化により自然に線形代数が出てきたのがわかるかと思います。

この、「現在の温度分布を表すベクトルに行列をかけると次のステップの温度分布が出てくる」という計算を素直にコードに落とすとこんな感じになるでしょう。後で使うのでscipyからlinalgをインポートしてあります。

import copy

import matplotlib
import matplotlib.pyplot as plt
from scipy import linalg
import numpy as np

N = 32
h = 0.1
v = np.array([min(x, N-x) for x in range(N)], dtype='float64')
A = np.zeros((N, N))

# 行列Aを作る
for i in range(N):
    i1 = (i + 1) % N
    i2 = (i - 1 + N) % N
    A[i][i] = 1.0 - 2.0*h
    A[i][i1] = h
    A[i][i2] = h

r = []
for i in range(1000):
    v = A.dot(v) # Aをかけると次のステップの状態が得られる
    if (i % 100) == 0:
        r.append(copy.copy(v))

for s in r:
    plt.plot(s)

実行すると先ほどと同じ結果が得られます。

さて、せっかく時間発展を表現する行列が得られたので、その行列の性質と時間発展の関係を見てみましょう。

この行列$A$の$i$番目の固有値と、対応する固有ベクトルをそれぞれ$\lambda_i$と$\vec{e}_i$で表現しましょう。

ここで、固有値は絶対値の大きい順に並んでいるものとします。すなわち$\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_N$です。

まず、初期条件を表すベクトルを$\vec{v}_0$としましょう。これを行列$A$の固有ベクトルの線形結合で以下のように表現できたとします。

\vec{v}_0 = c_1 \vec{e}_1 + c_2 \vec{e}_2 + \cdots c_N \vec{e}_N

これにAをかけてみましょう。

A \vec{e}_i = \lambda_i \vec{e}_i

ですから、

\vec{v}_1 = A \vec{v}_0 = c_1 \lambda_1 \vec{e}_1 +
c_2 \lambda_2  \vec{e}_2 + \cdots
c_N \lambda_N  \vec{e}_N

となります。

$A$を$n$回かけるとこんな感じです。

\vec{v}_n = c_1 \lambda_1^n \vec{e}_1 +
c_2 \lambda_2^n  \vec{e}_2 + \cdots
c_N \lambda_N^n  \vec{e}_N

ここで、行列$A$の最大固有値を求めてみましょう。PythonならSciPyを使えばあっという間です。

w, v = linalg.eigh(A, eigvals=(N-1,N-1))
print(w) #=> [1.]

1.0が出てきました。すなわち、この行列の最大固有値は1です。linalg.eigh(A, eigvals=(N-2,N-2))とすると、二番目に大きな固有値を得ることができますが、その値は$0.99615706$です。また、最小の固有値は$0.6$です。つまり、最大固有値が$\lambda_1 = 1$で、それ以外はすべて真に1より小さい、つまり$0 < \lambda_i < 1 \quad (i\neq 1)$が成り立ちます。従って、何度も$A$をかけると、最大固有値に対応するベクトル以外の成分は消えます。

\lim_{n \rightarrow \infty} A^n \vec{v}_0 = c_1 \vec{e}_1

先ほど得られた固有ベクトルも見てみましょう。

w, v = linalg.eigh(A, eigvals=(N-1,N-1))
print(v)

[[-0.1767767]
 [-0.1767767]
 [-0.1767767]
 [-0.1767767]
 [-0.1767767]
(snip)
 [-0.1767767]
 [-0.1767767]]

全て同じ値($-1/\sqrt{32}$)になっています。つまり、一様な温度ということです。このベクトルと、初期条件ベクトルの内積をとれば、係数$c_1$が求まり、すぐに定常状態$c_1 \vec{e}_1$が求まることになります。

熱伝導方程式を離散化すると、状態がベクトルに、時間発展は行列をかけることに対応し、時間発展行列の最大固有状態が定常状態に対応することがわかったかと思います。

シュレーディンガー方程式

カリキュラムによりますが、理工系の大学ならどこかで量子力学を学ぶことになるでしょう。時間非依存・一体・一次元のシュレーディンガー方程式は以下のように書けます。

$$
\left(
\frac{-\hbar^2}{2m} \frac{d^2 }{d x^2} + V(x)
\right) \psi(x) = E \psi(x)
$$

ここで、$\hbar$はプランク定数、$m$は質量、$V(x)$はポテンシャル、$\psi(x)$が波動関数です。例えば$V$として井戸型ポテンシャルを取ると、閉じ込めによりエネルギーが少し上がること、井戸の外に波動関数が少ししみ出すことなど、量子力学特有の不思議な現象が起きます。量子力学において重要なのは、一番エネルギーの低い基底状態と呼ばれる状態です。この方程式を離散化し、数値的に解くことで基底状態を求めてみましょう。面倒なので$\hbar^2/2m$を$1$とする単位系を取りましょう。系を離散化し、波動関数$\psi(x)$をベクトル$\vec{v}$で表現します。先程のシュレーディンガー方程式を、熱伝導方程式と同様に離散化すると

$$
-v_{i+1} + 2 v_i - v_{i-1} + V_i v_i = E v_i
$$

となります。ただし、$V_i$は、$V(x)$を離散化した時の$i$番目の要素です。これは、行列とベクトルで書くこともできます。

$$
H \vec{v} = E \vec{v}
$$

ただし、$H$は以下のような要素を持つ行列です。

こうして、シュレーディンガー方程式を離散化することで、行列の固有値問題に落ちました。これを解くと波動関数が求まります。早速基底状態を求めてみましょう。Pythonを使えば楽勝です。世の中を32分割し、井戸型ポテンシャルの深さ$d$は$5$くらいにして、8から16まで$-d$、それ以外は0という形にしましょう。たとえばこんなスクリプトになるでしょう。

import matplotlib.pyplot as plt
from scipy import linalg
import numpy as np

N = 32
A = np.zeros((N, N))
d = 5.0
V = np.array([-d if i in range(N//4, 3*N//4) else 0 for i in range(N)])
for i in range(N):
    i1 = (i + 1) % N
    i2 = (i - 1 + N) % N
    A[i][i] = 2.0 + V[i]
    A[i][i1] = -1
    A[i][i2] = -1
w, v = linalg.eigh(A)
v = v.transpose()
i0 = np.argmax(abs(w))
v0 = np.power(v, 2)[i0]
plt.plot(v0*20+w[i0])
print(w[i0])
plt.plot(V)

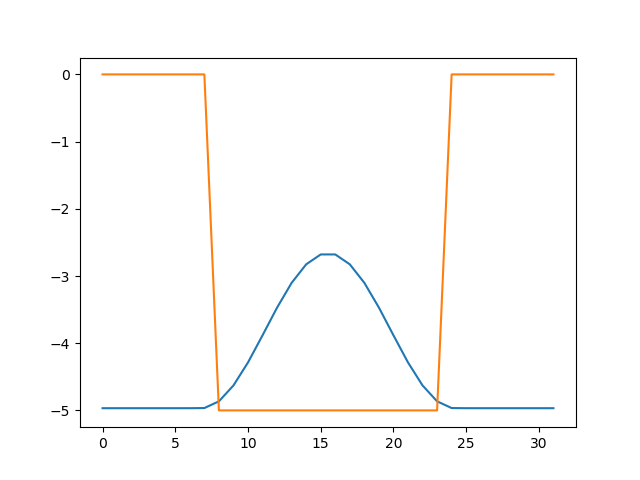
これは、先程の行列の絶対値最大固有値と対応する固有ベクトルを求め、絶対値最大固有値を表示し、固有ベクトル(波動関数)をポテンシャル関数とともにプロットするスクリプトになっています。

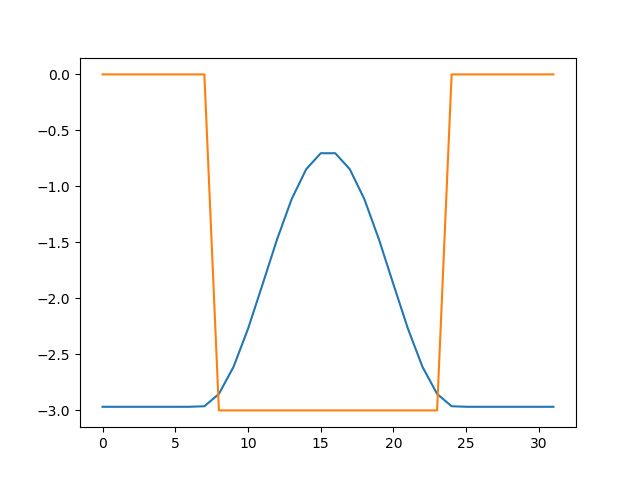
実行すると、固有値-4.9672674197348705の他に、以下のような図が出力されると思います。

ポテンシャルの形がオレンジで、波動関数の二乗が青で描いてあります。波動関数は20倍に誇張してあります。井戸の中に電子が閉じ込められており、少し井戸の外側に染み出していること、固有エネルギーが、ポテンシャルの底(-5.0)よりも、若干高い(-4.97)ことがわかります。このように、ポテンシャルに閉じ込められた状態を束縛状態といいます。

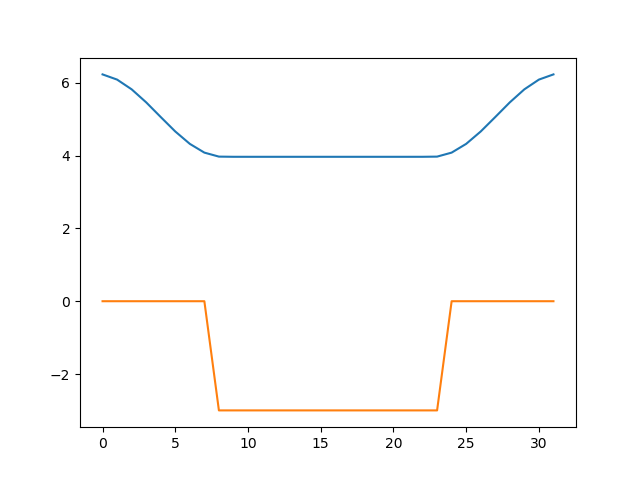
さて、ここまでは楽勝でした。では、ポテンシャルの底を少し浅くしてみましょう。どうなるでしょうか？先程のスクリプトを$d=3$にして再度実行してみます。

何かおかしなことになりました。固有値も負ではなく、正の値(3.967956931783471)になっています。波動関数の二乗ではなく、生の波動関数を表示してみましょう。

基底状態では節が無いはずの波動関数がばたついています。実はこれは、束縛されていない、自由な電子の状態を拾っています。もともとのシュレーディンガー方程式において、井戸の中の状態は離散化され、エネルギーは飛び飛びの値をとります。しかし、ある程度以上のエネルギーを持つ電子は井戸に束縛されておらず、自由に飛び回ることができます。この時のエネルギー準位は連続値を取りますが、離散化によりこちらも飛び飛びの値になります。井戸の中に束縛された電子のエネルギー準位が離散的なのはもともとの方程式の特性ですが、井戸に束縛されていない電子のエネルギー準位が離散的になるのは、方程式を離散化した影響、いわばフェイクです³。

これを解決するには、絶対値最大ではなく、最小の固有値を拾ってくればOKです。

# i0 = np.argmax(abs(w)) ↓以下に修正
i0 = np.argmin(w)

正しい基底状態を拾うことができました。

ここではすべての固有状態を求めているため、「最初から最小の固有値と対応する固有状態を求めれば良いじゃないか」と思うかもしれません。しかし、一般の問題では全部の固有値を求めるのは計算が重すぎるため、一部の固有値だけを求めるということがよく行われます⁴。その際、もっとも簡単な方法が、絶対値最大の固有値と固有状態を求める累乗法(Power Method)と呼ばれる方法です。この方法は簡単ですが、ナイーブな方法では絶対値最大の固有値と固有状態しか求められないため、上記のような状態で「最小の固有値と対応する固有状態」を求めたい時には工夫が必要になります。

一般に、何か方程式を離散化して解く時、多くの場合においてそのままライブラリに放り込めば解けます。しかし、状況によっては変なことが起きることがあります。その時に「何が起きたか」「何が原因か」「正しい解を得るにはどうすればよいか」を考えるためには、量子力学だけでなく、線形代数の知識も必要となります。ここでは固有値問題の題材として量子力学を取り上げましたが、応用面において固有値問題が頻出するのは有限要素法でしょう。建物の構造解析や、材料の強度のチェックなど、産業応用で有限要素法は欠かせません。有限要素法を扱うためのライブラリやアプリケーションは多数存在します。しかし、有限要素法における前処理や、反復解法の性質を知らないと収束が遅くなったり、おかしなことが起きても気づかない、なんてことがおきます。そのためにも線形代数の知識は必須です。

運動方程式

先の二つの例では空間を離散化することで行列やベクトルが出てきましたが、今回は時間の離散化を見るために運動方程式を考えてみます。

以下のようなハミルトニアンを考えます。

$$
H = p^2/2 + q^2/2
$$

$p$が一般化運動量、$q$が一般化座標で、これは調和振動子を記述するハミルトニアンです。ハミルトンの運動方程式は以下のように書けます。

\begin{align}
\dot{p} &= -q \\
\dot{q} &= p
\end{align}

これは、以下のように行列の形でも書けます。

\frac{d}{dt}
\begin{pmatrix}
p \\
q
\end{pmatrix}
=
\begin{pmatrix}
0 & -1 \\
1 & 0 
\end{pmatrix}
\begin{pmatrix}
p \\
q
\end{pmatrix}
= L
\begin{pmatrix}
p \\
q
\end{pmatrix}

ただし、$L$は

L=
\begin{pmatrix}
0 & -1 \\
1 & 0 
\end{pmatrix}

です。この方程式を形式的に解くと

\begin{pmatrix}
p(t) \\
q(t)
\end{pmatrix}
=
\exp{(tL)}
\begin{pmatrix}
p(0) \\
q(0)
\end{pmatrix}

ここで、

\exp{(tL)}
= I + tL + \frac{t^2 L^2}{2!} + \cdots
+ \frac{t^n L^n}{n!} + \cdots

です。一般には指数関数の肩に行列が乗ったものは厳密に計算できませんが、今回は計算できます。

\exp{(tL)}
=
\begin{pmatrix}
\cos t & \sin t \\
-\sin t & \cos t
\end{pmatrix}

つまり、これは原点を中心として時計回りの回転になります。さて、この厳密解を知らないものとして、時間発展を離散化してみましょう。以下、時間刻みを$h$とし、時刻$t$から$t+h$の状態を求めることを繰り返すことで時間発展させることにします。

最も簡単なのは一次のオイラー法です。それはこんな式で書けます。

\begin{align}
p(t+h) &= p(t) - h q(t) \\
q(t+h) &= q(t) + h p(t) \\
\end{align}

行列表示するとこうなります。

\begin{pmatrix}
p(t+h) \\
q(t+h)
\end{pmatrix}
=
\begin{pmatrix}
1 & -h \\
h & 1
\end{pmatrix}
\begin{pmatrix}
p \\
q
\end{pmatrix}
\equiv \tilde{U}_E
\begin{pmatrix}
p \\
q
\end{pmatrix}

これは、厳密解を$t$に関して一次までテイラー展開していることに対応していることがわかります。しかし、この方法で計算すると、どんどんエネルギーが増えて行きます。

import matplotlib.pyplot as plt
  
vq = []
vp = []
h = 0.05

q = 1.0
p = 0.0
for i in range(1000):
    (tp, tq) = (p, q)
    (p, q) = (tp - h * tq, tq + h * tp)
    vp.append(p)
    vq.append(q)

plt.plot(vq, vp)

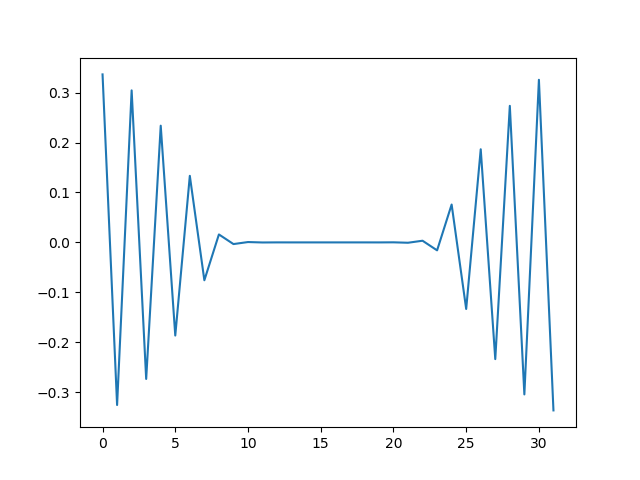
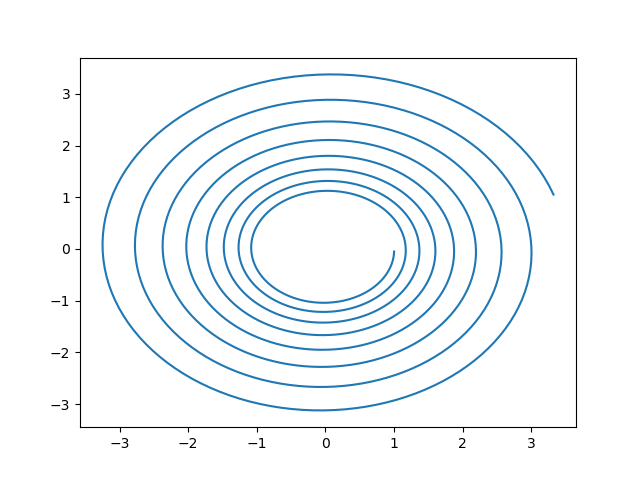
本来、円を描くはずの軌道が螺旋を描きながらエネルギー(半径)が大きくなっています。

なぜエネルギーが大きくなるかというと、時間発展を記述する行列$\tilde{U}_E$の行列式が$1$より大きいからです。実際に行列式を計算してみると、

$$
|\tilde{U}_E| = 1 + h^2 > 1
$$

と1より大きいため、この行列が引き起こす写像が、面積を増加させていることがわかります。面積が増える、すなわち空間を引き伸ばしているので、エネルギーも単調に増えていきます。

次に、運動方程式を離散化する際によく行われるシンプレクティック積分を試してみましょう。一次のシンプレクティック積分は以下のようにかけます。

\begin{align}
p(t+h) &= p(t) - h q(t) \\
q(t+h) &= q(t) + h p(t+h) \\
\end{align}

次のステップの$q$を計算する際、すでに更新した$p$を使うのがポイントです。計算してみましょう。

import matplotlib.pyplot as plt
  
vq = []
vp = []
h = 0.05

q = 1.0
p = 0.0
for i in range(1000):
    p = p - h * q
    q = q + h * p
    vp.append(p)
    vq.append(q)

plt.plot(vq, vp)

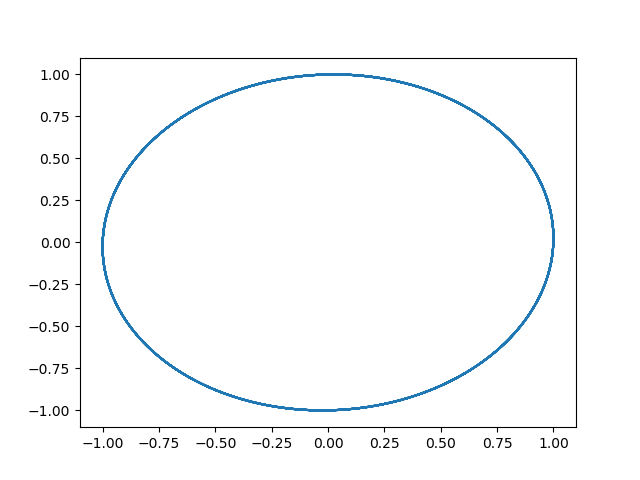
軌道が閉じて円になり、エネルギーが発散しなくなりました。先程の方程式を行列表示してみましょう。

\begin{pmatrix}
p(t+h) \\
q(t+h)
\end{pmatrix}
=
\begin{pmatrix}
1 & -h \\
h & 1 - h^2
\end{pmatrix}
\begin{pmatrix}
p \\
q
\end{pmatrix}
\equiv \tilde{U}_S
\begin{pmatrix}
p \\
q
\end{pmatrix}

全体としてのテイラー展開の精度は1次ですが、一つだけ二次まで展開されています。時間発展を記述する行列$\tilde{U}_S$の行列式は

$$
|\tilde{U}_S| = 1 - h^2 + h^2 = 1
$$

と、厳密に1になっています。軌道は厳密解からずれているものの、近似された時間発展演算子(を記述する行列)は、変換の前後で面積要素を厳密に保存します。これがシンプレクティック積分の特徴です。この性質により、エネルギーが厳密な値から揺らぐものの、一方的に増加もしくは減少しないため、安定に長時間積分できます。

今回は調和振動子を扱ったので、時間発展演算子が行列で表現できましたが、一般には非線形になるために行列では表現できません。しかし、時間発展演算子が空間の面積(体積)を保存するかどうかは、時間発展のヤコビ行列式が1になるかどうかで判断できます。このように、運動方程式の数値積分という分野にも線形代数が顔を出すことがわかります。

シンプレクティック積分に興味がある方は解析力学の幾何学的側面シリーズを参照してください。

線形安定性解析

線形偏微分方程式は解くことができますが、非線形の微分方程式は一般には解くことができません。でも、その微分方程式で記述された系の性質を調べたい場合があります。そのような時に使うのが線形安定性解析です。

車が渋滞する状況を記述する、最適速度模型(Optimal Velocity Model)という模型があります。サーキットの中を$N$台の車が同じ方向に進んでいる状況を考えます。$n$番目の車の位置と速度を$x_n$、$v_n$とすると、最適速度模型は以下のような微分方程式で記述されます。

\begin{align}
\dot{v_n} &= a \left(V(x_{n+1}-x_n) - v_n \right) \\
\dot{x_n} &= v_n
\end{align}

ただし$V(x)$は、最適速度関数と呼ばれる関数で、以下のように定義されます。

$$
V(x) = \tanh(x-2) - \tanh(2)
$$

この模型は、「自分の前の車を見て、車間距離から決まる最適速度に合わせてアクセルやブレーキを踏む」というドライバーの振る舞いをモデル化したもので、パラメータによってスムーズに流れたり、渋滞ができたりします。詳しくは紹介記事を書いたのでそちらを参照してください。

さて、この方程式は非線形であり、厳密解を得ることは困難です。しかし、「全員が等間隔に並び、その車間距離で決まる最適速度で走っている状況」が、この方程式の解であることがわかります。

いま、サーキットの全長を$L$としましょう。$N$台の車が等間隔に並ぶと、車間距離は$b \equiv L/N$です。この車間距離での最適速度は$\bar{v} = V(b)$です。各車が車間距離$b$だけあけて、それぞれ最適速度$\bar{v}$ぴったりで走っている時は、$\dot{v}_n = 0$、すなわち速度変化がなく、一定速度で走っている状態になります。全員が同じ速度で走っているので車間距離も変化せず、同じ車間距離を保ったまま回り続けます。この解を一様流解といいます。一様流解は以下のような式で表現できます。

\begin{align}
v_n &= \bar{v} \\
x_n &= \bar{v}t + bn
\end{align}

さて、一様流解の状態で、誰かがブレーキもしくはアクセルを踏んだとしましょう。その「乱れ」は増幅されるでしょうか？それとも時間とともに消えていくでしょうか？それを調べるのが線形安定性解析です。

一様流解の状態から、それぞれ速度が$\delta v_n$、位置が$\delta x_n$だけずれた状態を考えましょう。ずれが小さいと思うと、

$$
U(x_{n+1} - x_n) \sim U(b) + U'(b) (\delta x_{n+1} - \delta x_{n})
$$

と展開できます。すると、運動方程式が、$\delta v_n$と$\delta x_n$に関する連立微分方程式、

\begin{align}
\dot{\delta v_n} &= a   U'(b) (\delta x_{n+1} -  \delta x_{n}) - \delta v_n\\
\dot{\delta x_n} &= \delta v_n
\end{align}

と書けます。$\delta v_n$と$\delta x_n$の時間微分が$\delta v_n$と$\delta x_n$の線形結合でかけていますから、これは方程式が線形化されたことを意味します。

したがって、$\delta v_n$と$\delta x_n$を並べたベクトル$\vec{z}$に関する時間発展だと思うと、適当な行列$L$を用いて

$$
\frac{d \vec{z}}{dt} = L \vec{z}
$$

と書くことができます。この方程式の安定性は、$L$の最大固有値の実部で決まります。これはフーリエ級数により求めることができて、$N$が十分大きい時の線形安定条件

$$
a > 2 V'(b)
$$

が得られます。

計算の詳細については原著論文を参照してください⁵。

まとめ

本稿では、主に数値計算における線形代数の有用性を紹介するため、熱伝導方程式、シュレーディンガー方程式、ハミルトンの運動方程式、そして最適速度模型を取り上げました。線形代数の有用性というか、要するに微分方程式をなんかしようと思うと、ほぼ間違いなく線形代数が顔を出すということがなんとなくわかっていただけたかと思います。

私はAIの専門家ではないので確かなことは言えませんし、「AI人材」というのが何を意味するのか私にはわかりません。線形代数があやふやでも、TensorFlowやChainerといったフレームワークを使って成果を出すことはできるでしょう。ただ、「AI人材」というのを「とりあえずフレームワークを使える人材」もしくは「必要に応じて計算の定義に立ち返って検証したり、新たなフレームワークを構築できる人材」と定義するならば、個人的には学生さんは後者を目指して欲しいな、という気がしています。

しつこいですが線形代数は広範な範囲にまたがって活躍する重要な学問です。ここで挙げた例以外にも様々な分野で出てきます(例えばCGとか)。線形代数には、ここで紹介した用語(主に固有値や固有ベクトル)の他にも「行列のランク」「対角和(トレース)」「正則性」など、初学者にとっては「計算方法や定義はわかったけど、それってなんの役に立つのさ？」という用語が多数出てきます。もちろん重要だからそういう用語が定義されるのですが、それらの紹介をする前に執筆者が力尽きました。他の方による記事の投稿を待つことにします。

1. 後で関数の内積を使いたいのでカッコを使っていますが、内積とベクトルの表記がごっちゃになっていますね。まぁ文脈でわかると思うのでこのままにします。 ↩

2. シンプルに書くために非効率的に書いています。 ↩

3. 実際には空間を有限に限定していることにより自由電子の準位も離散化されますが、今回のケースでは離散化による影響の方が大きいです。 ↩

4. そもそも波動関数のベクトルを数本メモリに格納するのがやっとで、ハミルトニアンをまるごと保持するのは不可能であるような大きい問題を解くことも多いです。その場合はハミルトニアンの全対角化はかなり厳しくなります。 ↩

5. すみません、この記事でちゃんと線形安定性解析をやろうと思ったのですが、ここで力尽きました。 ↩