これはU-TOKYO AP Advent Calendar 2017の24日目の記事です。いま見たらまだ空いてたので、23日の記事の続きを書いてみましょう。
空間について
解析力学では位相空間を考えます。適切な位相空間を考えることで系の状態がその空間の一点で表現され、時間発展は点の移動として表現されます。その空間について考えてみましょう。
今、二つの自由度$q_1, q_2$で表現される系を考えます。これは二次元空間の位置だと思ってもいいですし、二重振り子の二つの角度だと思ってもかまいません。さて、$q_1, q_2$で張られた空間を考えます。この空間を状態空間$M$と呼びましょう。さて、よく知られているように運動方程式は二階微分方程式ですから、この空間だけでは運動を記述することはできません。運動を記述するには、座標に対応する速度$\dot{q_1}, \dot{q_2}$が必要になります。
状態空間$M$は一般には曲がっているため、ある状態点$Q(q_1, q_2)$における速度と、別の点における速度は異なる意味を持ちます。つまり、それぞれの点$Q$において、別々の速度が定義されていると考えるべきです。
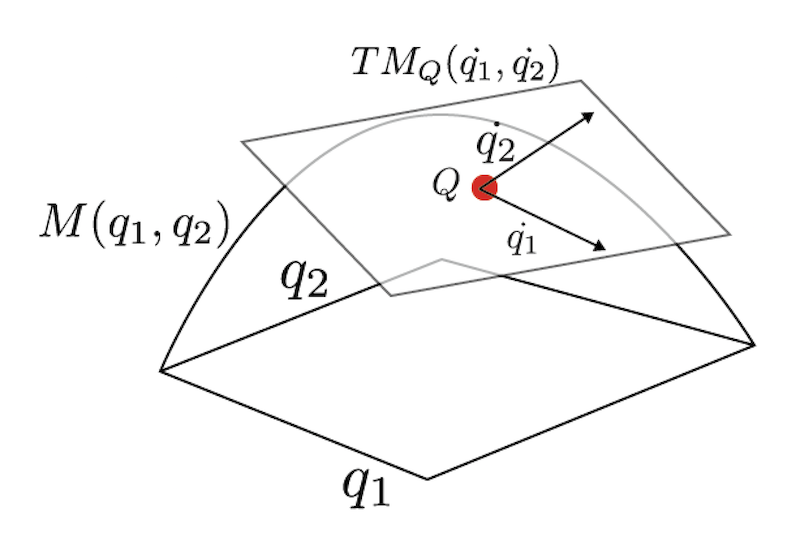
ある点$Q$において、その点における速度$\dot{q_1}, \dot{q_2}$が作る空間を$TM_Q(\dot{q_1}, \dot{q_2})$と呼び、$M$の点$Q$における接空間(tangent space)と呼びます。また、$M$上の点における接空間を集めた集合がなす空間を接バンドル(tangent bundle)と呼び、$TM$で表します。図解するとこんな感じです。
$q_1, q_2$で張られる空間$M(q_1, q_2)$があり、ある点$Q$に接する接平面は$TM_Q(\dot{q_1}, \dot{q_2})$は速度ベクトル$(\dot{q_1}, \dot{q_2})$で張られており、その接平面を全部合わせた空間が接バンドル$TM$です。接バンドル$TM$は$(q_1, q_2, \dot{q_1}, \dot{q_2})$で張られています。より正確には、まず$(q_1, q_2)$で接空間が指定され、その中の点を$\dot{q_1}, \dot{q_2}$で指定します。
さて、運動方程式とはそれぞれの速度の時間微分を定義することです。
\begin{align}
\ddot{q_1} &= f_1 \\
\ddot{q_2} &= f_2
\end{align}
この力は自由度の数だけ必要ですが、ラグランジアン$L(q_1, q_2, \dot{q_1}, \dot{q_2})$を考えると、その変分から$f_1$や$f_2$といった必要な力が全部出てくる、ということを解析力学で学んだと思います。すなわち、ラグランジアンは接バンドル$TM$に住んでいます。
さて、詳細は省きますが、接空間$TM_Q$を貼るベクトルは実は$\partial/\partial q_1$と$\partial/\partial q_2$です。つまり、接空間$TM_Q$上のベクトル$(v_1, v_2)$は、
(v_1, v_2) = v_1 \frac{\partial}{\partial q_1} + v_2 \frac{\partial}{\partial q_2}
と表現されます。微分形式を学んだかと思いますが、上記のベクトルに対応するコベクトルを次のように定義することができます。
\left(
\begin{matrix}
p_1\\
p_2
\end{matrix}
\right)
= p_1 dq_1 + p_2 dq_2
ここで、$\partial / \partial q_i$と$dq_j$の間に自然な内積
\left<
\frac{\partial}{\partial q_i}, dq_j
\right>
\equiv
\frac{\partial q_j}{\partial q_i}
= \delta_{ij}
が定義できることに注意しましょう。この変換により、 接空間$TM_Q$には、自然に$dq_1, dq_2$が張る空間が定義できることになります。この空間を余接空間(cotangent space)と呼び、$T^*M_Q$で表します。$M$上の全ての点における余接空間を集めた空間が余接バンドル(cotangent bundle)で、$T^*M$で表されます。
もうお気づきだと思いますが、この空間は$(q_i, \dot{q_i})$からルジャンドル変換で$(q_i,p_i)$に移った世界です。ハミルトニアン$H$は、この余接バンドル$T^*M$に住んでいます。
リュービル演算子のエルミート性について
前の記事において、ハミルトンの運動方程式は位相空間に速度場を導入すること、その速度場はdivergence freeであることから、流れが非圧縮であることを紹介しました。それをリュービル演算子の観点から見てみましょう。以下では一自由度のハミルトン系$H(p,q)$を考えることにします。
リュービル演算子とは、時間微分演算子のことで、以下のように定義されます1。
i L A = \frac{d A}{d t}
ここで、$A(p,q)$の時間微分は
\frac{d A}{d t} =
\dot{q} \frac{\partial A}{\partial q}
+
\dot{p} \frac{\partial A}{\partial p}
ですから、リュービル演算子は
i L = \dot{q} \frac{\partial }{\partial q}
+
\dot{p} \frac{\partial }{\partial p}
と表現することができます。さて、この演算子がエルミートである条件を考えましょう。ある内積$(f, g)$を考えた時に
(iL f, g) = (f ,iL g)
と、演算子を左右どちらにかけても同じ結果になる時、この演算子$iL$はエルミートであると言います。
いま、位相空間が$(p,q)$で張られているので、この世界の関数の内積$(f,g)$を
(f, g) = \int f^* g dp dq
で定義しましょう。先程のリュービル演算子の定義を放りこんで計算すると、
\begin{align}
(f, iL g) &= \int f^* (iL) g dp dq \\
&= \int f^* \left(
\dot{q} \frac{\partial }{\partial q}
+
\dot{p} \frac{\partial }{\partial p}
\right) g dp dq \\
&= (iL f, g) - \int fg
\left(
\frac{\partial \dot{q}}{\partial q} +
\frac{\partial \dot{p}}{\partial p}
\right) dp dq
\end{align}
となります。ただし、途中で$p$と$q$についてそれぞれ部分積分を使い、かつ境界でゼロを仮定しています。さて、リュービル演算子がエルミートであるためには、部分積分で出てきたゴミがゼロでなければいけませんから
\frac{\partial \dot{q}}{\partial q} +
\frac{\partial \dot{p}}{\partial p}
= 0
でなければなりません。これは先の記事で出てきた位相空間での流れ場の非圧縮条件にほかなりません。つまり、ハミルトンの運動方程式が位相空間に非圧縮な流れ場を作るということは、リュービル演算子がエルミートであるということと等価になります。
流れ場について
さて、ベクトル解析で、divergenceがゼロであるような流れはポテンシャルで書けるということを習ったと思います。ハミルトンの運動方程式でも同様なことが書けます。
まず、ハミルトニアン$H$の勾配、$\nabla H$を考えましょう。具体的にはこんな形になります。
\nabla H =
\left(
\begin{matrix}
\partial_p H \\
\partial_q H \\
\end{matrix}
\right)
これを使って、運動方程式はこのように書けます。
\left(
\begin{matrix}
\dot{p} \\
\dot{q}
\end{matrix}
\right)
=
\Omega \nabla H
ただし、ここで$\Omega$は以下のような反対称行列です。
\Omega =
\left(
\begin{matrix}
0 & -1 \\
1 & 0
\end{matrix}
\right)
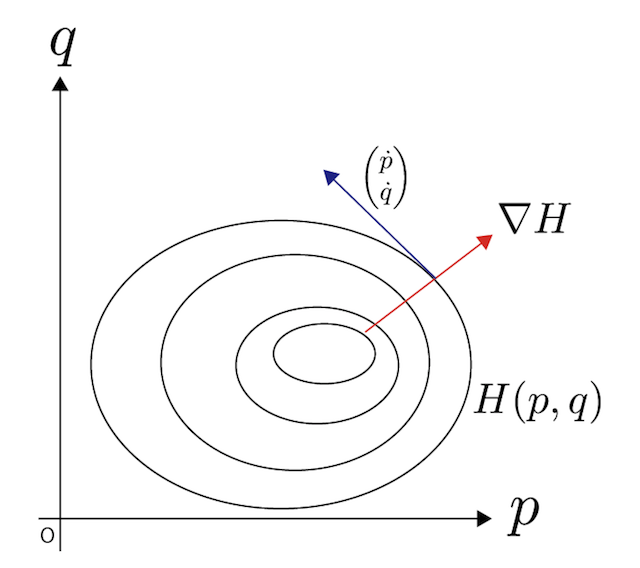
つまり、ハミルトンの運動方程式とは、位相空間に定義されたスカラー関数$H$の勾配を、90度回転させたもの、ということになります。
上図を見ると分かる通り、位相空間における点の速度ベクトルは、必ずハミルトニアンの勾配に直交しています。ハミルトニアンの勾配に直交しているのだから、この運動はハミルトニアンの値を変えません。これが、ハミルトンの運動方程式においてハミルトニアンが時間不変量になる直感的な理由となります。
まとめ
解析力学の幾何学的な側面の続きを書いてみました2。まとめると
- 我々の目に見える自由度で張られた空間が状態空間$M$
- 速度ベクトルを考慮した空間が接バンドル$TM$で、ラグランジアンはそこに住んでいる
- 接空間に共役な空間である余接空間を集めた空間が余接バンドル$T^*M$で、ハミルトニアンはそこに住んでいる。
- 時間発展がシンプレクティックであることとリュービル演算子がエルミートであることは等価である
- ハミルトンの運動方程式で位相空間が進む方向ベクトルはハミルトニアンの勾配に直交する向きとなっており、それ故にこの運動でハミルトニアンは保存される
といった感じです。そういう意味でハミルトンの運動方程式は、広い意味で「回転」を記述していると言えるかと思います。ある軸のまわりに回転させる変換では、その軸から点までの距離(半径)が保存されます。その半径がハミルトニアンにあたります。実は、ハミルトニアン$H$と時間$t$も含めた拡張位相空間を考えると、この回転というイメージがよりわかりやすくなるのですが、この辺で力尽きました。詳細は参考文献を読んで下さい。
参考
- 解析力学1, 2 (中村孔一、山本義隆著, 朝倉物理学大系) ←もし解析力学に興味があるなら読んで絶対に損はしないし、買って手元においておくべき本だと思います(個人の感想です)。