はじめに
あるデータセットの分布(確率密度関数)を見たいときに、ヒストグラムを作るのは面倒くさい。最初に最小値と最大値を調べないといけないし、分散の小さい正規分布などでは、中央付近のビンは細かく、その他は粗くとらないときれいな分布が見えない。そういう場合は確率密度関数ではなく、累積分布関数を見るほうが楽だしきれいだ。累積分布関数はソート一発で求めることができる。
方法
データが配列dataに入っているとする。これをソートして、
(データの値, そのデータの位置の割合)
をプロットすると、それが累積分布関数になる。コードにするとこんな感じ。
# 配列dataにデータが入っている
data.sort!
n = data.size
n.times do |i|
puts "#{data[i]} #{i.to_f/n.to_f}" # これが累積分布関数になる
end
原理
確率密度関数(probability density function、PDF) $f(x)$の原始関数 $F(x)$ が累積分布関数(cumulative distribution function, CDF)であり、以下のように定義される。
F(x) = \int_{-\infty}^x f(x) dx
累積分布関数の定義から明らかなように、ある確率変数$X$が、ある値$x$以下の値を取る確率が$F(x)$で与えられる。いま、$N$個のサンプルがあったとして、ある値$x$より小さいデータが$m$個あったとするならば、この確率変数の累積分布関数$F(x)$は$m/N$と推定できる。データが昇順にソートしてあれば、あるデータが$i$番目にあったならば、そのデータを含めてそれより小さいデータは$i$個あるのだから$i/N$が累積分布関数の推定値を与える。
サンプル
いくつかの分布について例を挙げる。
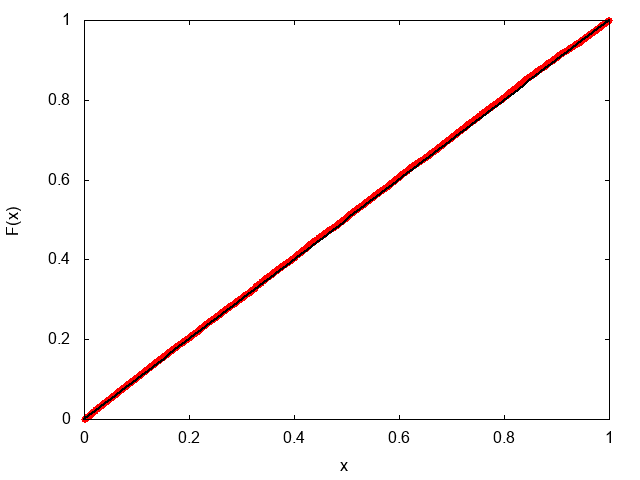
一様分布
rand()をそのままdataにpushすれば、一様分布になる。
data = []
10000.times do
data.push rand()
end
この時、分布関数は$f(x) = 1$であるので、累積分布関数は$F(x) = x$となる。プロットするとこんな感じ。
赤点がデータ、黒の実線が理論曲線。
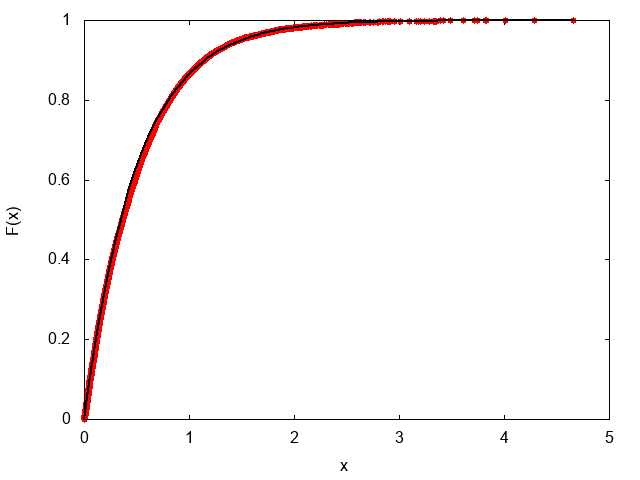
指数分布
一様乱数を$r$として、$-\log(1-r)/\lambda$とすると、パラメータ$\lambda$の指数分布となる。
data.push -Math::log(1.0-rand())/lambda
分布関数は$f(x) = \lambda e^{-\lambda x}$、累積分布関数は$F(x) = 1 - e^{-\lambda}$となる。
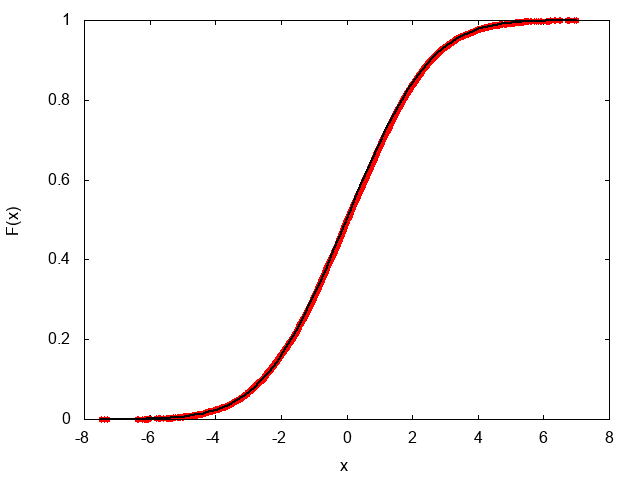
ガウス分布
一様乱数からガウス分布を作るには、ボックス=ミュラー法を使う。一様乱数$r_1, r_2$から、平均0、標準偏差$\sigma$のガウス分布を作るには$\sigma \sqrt{-2 \log(r_1)} \cos(2 \pi r_2)$とすれば良い。
r1 = rand()
r2 = rand()
data.push sigma*Math::sqrt(-2.0*Math::log(r1))*Math::cos(2.0*Math::PI*r2)
ソース
上記3つのデータを作る手抜きRubyスクリプトも掲載しておく。
def uniform(param)
rand()
end
def exp_dist(lambda)
-Math::log(1.0-rand())/lambda
end
def gaussian(sigma)
r1 = rand()
r2 = rand()
sigma*Math::sqrt(-2.0*Math::log(r1))*Math::cos(2.0*Math::PI*r2)
end
def make_dist(dist,param,filename)
puts filename
data = []
10000.times do
data.push dist.call(param)
end
data.sort!
n = data.size
open(filename,"w") do |f|
n.times do |i|
f.puts "#{data[i]} #{i.to_f/n.to_f}"
end
end
end
make_dist(method(:uniform),nil,"uniform.dat")
make_dist(method(:exp_dist),2.0,"exp.dat")
make_dist(method(:gaussian),2.0,"gaussian.dat")
上記をプロットするgnuplotファイル
set term png
set out "uniform.png"
set xla "x"
set yla "F(x)"
set ytics 0.2
set xtics 0.2
unset key
p "uniform.dat" pt 7 lc rgb "red"\
, x lc rgb "black" lw 2
set out "exp.png"
set xtics 1.0
p "exp.dat" pt 7 lc rgb "red"\
, 1-exp(-x*2) lc rgb "black" lw 2
set out "gaussian.png"
set xtics 2.0
p "gaussian.dat" pt 7 lc rgb "red"\
, (1+erf(x/sqrt(2)/2))/2 lc rgb "black" lw 2
以下のようにすればグラフが描画される。
$ ruby dist.rb
$ gnuplot plot.plt
まとめ
データがどういう分布をしているか見るのには、とりあえず累積分布関数を見るのが良いと思う。ソートするだけだし、確率密度関数を見るよりきれいな場合が多い。確率密度関数が欲しいときには、累積分布関数を数値微分して出したほうが、ヒストグラムから作るよりもきれいで簡単だと思う。
どうでもいいけど
誤差関数の定義って
\mathrm{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt
なんだけどさ、なんで
\mathrm{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2/2} dt
としなかったんだろうね。おかげで上記のプロットファイルでも、ガウス分布の理論曲線描く時に、
p "gaussian.dat" pt 7 lc rgb "red"\
, (1+erf(x/sqrt(2)/2))/2 lc rgb "black" lw 2
って余計なsqrt(2)が必要になって面倒くさい。