はじめに

ParaViewはオープンソースかつマルチプラットフォームな可視化ソフトウェアである。このParaViewで読むことができるVTKファイルフォーマットについてまとめる。

ソースは
https://github.com/kaityo256/paraview-sample
においてある。

ParaView

Windows/MacともにParaViewのインストールで苦労したことは無いので、すぐに入ると思う。公式サイト

から落としてインストールすればよい。

VTKフォーマット

ファイルの構造

VTK(Visualization Toolkit)ファイルフォーマットParaViewで読み込めるファイルフォーマットである。単純な形式であるレガシーフォーマット(Simple Legacy Format)と、XML形式の二種類あるが、ここでは単純なレガシーフォーマットのみ扱う。基本的には以下のPDFを読めば全部書いてある。

VTKレガシーファイルフォーマットは、こんな形式になっている。

# vtk DataFile Version 1.0
simple
ASCII
DATASET STRUCTURED_POINTS
DIMENSIONS 21 21 21
ORIGIN 0.0 0.0 0.0
SPACING 1.0 1.0 1.0

POINT_DATA 9261
SCALARS intensity float
LOOKUP_TABLE default
... (以下データ)

最初の行はファイルのバージョン情報。大文字小文字は区別し、バージョンをあらわす数字x.x以外の場所はこの通りに記述する必要がある。
次がファイルの名前。最大256文字。適当に書けばよいと思うが、個人的にはファイル名をここに記述している。
次がファイルフォーマット。ASCIIかBINARYを記述する。本稿ではASCIIフォーマットのみ説明する。
次がデータセットの構造。いくつか種類があるが、本稿では構造格子(Structured Grid)と非構造格子(Unstructured Grid)のみ扱う。
最後がデータセット。点データ(POINT_DATA)とセルデータ(CELL_DATA)があるが、本稿では主に点データを扱う。

データ構造

ファイルの四行目からはデータセットの構造を与える。一番単純な構造は構造格子(Structured Grid)で、以下のようなフォーマットを与える。

DATASET STRUCTURED_POINTS
DIMENSIONS 21 21 21
ORIGIN 0.0 0.0 0.0
SPACING 1.0 1.0 1.0

最初の行がデータセット(DATASET)の構造を指定する。ここでは構造格子(STRUCTURED_POINTS)を指定している。
次の行は、三次元直方体の三辺の点の数を与える。ここでは21×21×21の立方体構造を与えている。
ORIGINは、原点の座標を指定する。
SPACINGは、ひとつのグリッド(直方体形状)のサイズ。いわゆるアスペクト比で、昔はASPECT_RATIOと書いたが、今は非推奨。

これで三次元空間上に21×21×21=9261点の格子点が定義された。

データ点

格子が定義されたら、それぞれの格子上に定義される物理量を指定する。フォーマットはこんな感じになる。

POINT_DATA 9261

SCALARS intensity float
LOOKUP_TABLE default
0
0
0
0
....

最初に、これは点上に定義されたデータだと宣言する(POINT_DATA)
次からデータセット。いくつか種類があるが、本稿では主にスカラー量(SCALARS)とベクトル量(VECTORS)を扱う。
データセットは、「種類名前型」を指定する。最初の大文字の「SCALARS」は種類。次の「intensity」はデータの名前。自分でわかりやすいような名前をつければよい。最後が型。ここでは浮動小数点数「float」を指定している。
最後にデータの数だけデータをずらずら並べればよい。

サンプル1 単純球

フォーマットを理解するには、適当なVTKを吐くスクリプトを書いてみるのが早い。以下は、球の内部で、中心が1、表面が0となるような強度を持つようなスカラーデータを吐くスクリプト。

grid = 10
dim = grid*2+1
points = dim**3
r = 0.8

puts <<"EOS"
# vtk DataFile Version 1.0
test
ASCII
DATASET STRUCTURED_POINTS
DIMENSIONS #{dim} #{dim} #{dim}
ORIGIN 0.0 0.0 0.0
SPACING 1.0 1.0 1.0

POINT_DATA #{points}

SCALARS intensity float
LOOKUP_TABLE default
EOS

(-grid..grid).each do |iz|
  (-grid..grid).each do |iy|
    (-grid..grid).each do |ix|
    x = ix.to_f/grid
    y = iy.to_f/grid
    z = iz.to_f/grid
    v = r*r - (x*x + y*y + z*z)
    v = 0 if v < 0
    puts v.to_s
    end
  end
end

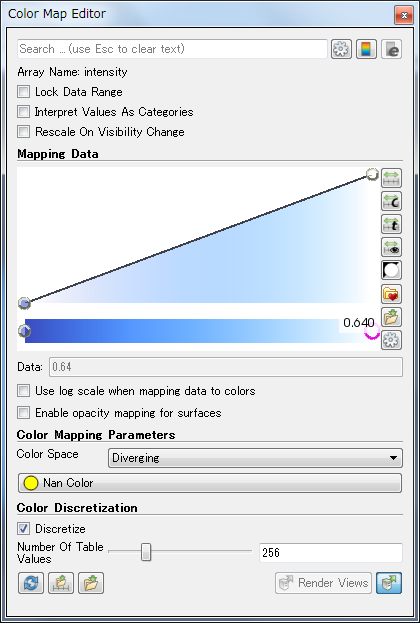
これをParaViewで読み込んで、Applyボタンを押した後、Representationを「Outline」から「Volume」にすると、以下のような表示なる。

ただし、色はColor Map Editorでこんな感じに指定している。

サンプル2 波動関数

単純な球ではつまらないので、波動関数(要するに球面調和関数)を表示してみよう。ソースはこんな感じ。

def export_vtk(filename,p)
  puts filename
  grid = 10
  dim = grid*2+1
  points = dim**3
  open(filename,"w") do |f|
    f.puts <<"EOS"
# vtk DataFile Version 1.0"
Wavefunction
ASCII
DATASET STRUCTURED_POINTS
DIMENSIONS #{dim} #{dim} #{dim}
ORIGIN 0.0 0.0 0.0
SPACING 1.0 1.0 1.0
POINT_DATA #{points}
SCALARS scalars float
LOOKUP_TABLE default
EOS
    for iz in -grid..grid
      for iy in -grid..grid
        for ix in -grid..grid
          x = ix.to_f/grid
          y = iy.to_f/grid
          z = iz.to_f/grid
          r = (x*x + y*y + z*z)**0.5
          f.puts p.call(x,y,z,r)
        end
      end
    end
  end
end

p_2pz = lambda{|x,y,z,r| Math.exp(-r*3.0)*(z)}
p_3dz2 = lambda{|x,y,z,r| Math.exp(-r*4.0)*(3*z**2 - r**2)}
p_3dzx = lambda{|x,y,z,r| Math.exp(-r*4.0)*(z*x)}

export_vtk("2pz.vtk",p_2pz)
export_vtk("3dz2.vtk",p_3dz2)
export_vtk("3dzx.vtk",p_3dzx)

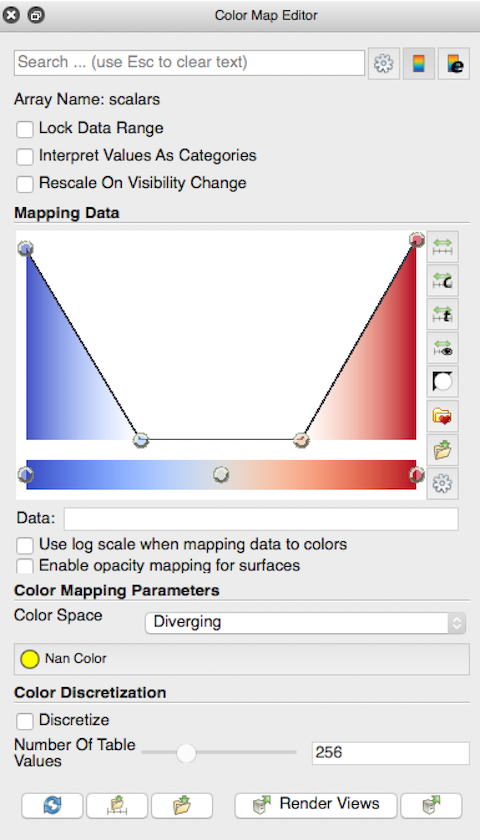
それぞれ2pz, 3dz2, 3dzx軌道を表示する。表示のためのColormapにちょっと工夫が必要だが、たとえば2pzなら、以下のような設定にすればよい。

値がゼロ付近は表示しないようにして、かつ波動関数の位相の正負を色で表現している。結果はこんな感じ。

同様に、3d$z^2$、3d$zx$軌道はこんな感じになる。

3d$z^2$

3dzx

個人的には3d$z^2$軌道が面白くて好き¹。

まとめ

VTKレガシーフォーマットを出力し、ParaViewで表示してみた。ここではフォーマットとしてはもっとも単純な構造格子を用い、可視化としてももっとも単純なVolumeを利用したが、他にもさまざまなことができる。特に連番のVTKファイルを与えてムービーを作る機能が便利なので、いろいろ試されたい。

本当はもうちょっとxy平面の軌道は中心付近に局在してるんだけど、色のつけ方によって中心に穴を開けて見せている。 ↩

ParaViewでVTKレガシーフォーマットを使う その1