はじめに
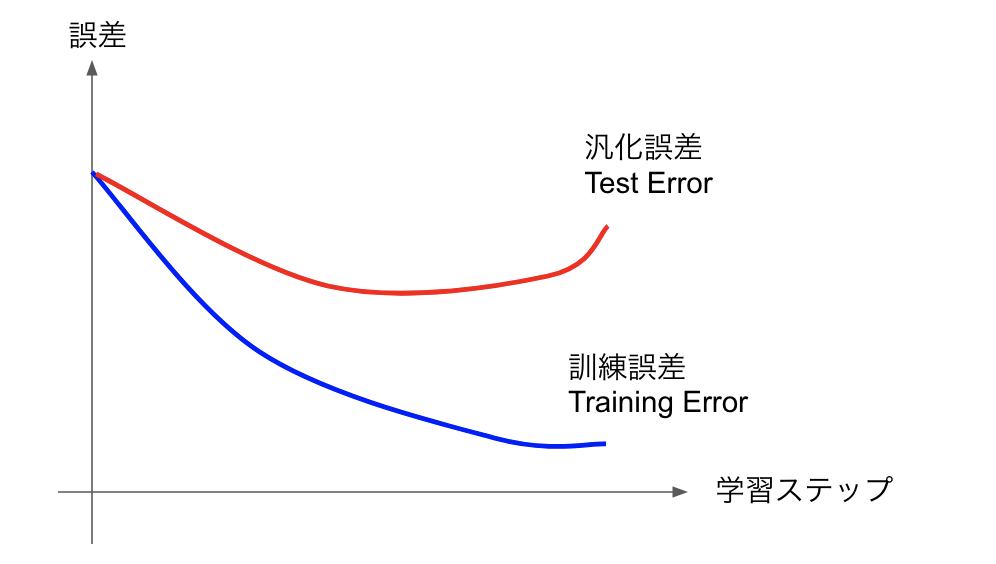
機械学習でよく出てくる図に、こんなのがあります。
学習が進む(もしくはモデルパラメータが増える)ほど訓練誤差(Training error)が低下する、つまりテストデータに対する予測精度は向上するが、テストのデータセットに入っていないデータに対する予測精度が下がり、汎化誤差(Test Error)が上がってしまうものです。いわゆる過学習(Over Fitting)という奴です。テストのデータ数が、モデルの自由度に比べて少ないほどこの傾向は顕著になります。
さていま、訓練データに対して「完璧」に学習が進んだとしましょう。つまり、理論的にはこれ以上ないほど過学習した状態を考えます。当然、訓練データが少ないほど、訓練データに対する予測はしやすくなりますから、訓練誤差は下がります。逆に、訓練データが少ないほど過学習しやすくなりますから、汎化誤差は増えるでしょう。訓練データを増やせば増やすほど、訓練誤差と汎化誤差の差は減っていくことが予想されます。また、「データ」は常にきれいとは限りません。だいたい何かしらの「ノイズ」が乗っていることでしょう。すると、テストデータの数を増やしていくと、最終的に精度は「ノイズの強さ」で頭打ちになりそうです。まとめると、
- 訓練データが少ないほど、訓練誤差は小さく、汎化誤差は大きくなる
- 訓練データが十分に多いと、訓練誤差も汎化誤差も、ノイズの強さで頭打ちになる
という感じです。直感にあう振る舞いですね。
この振る舞いは、簡単なケースなら厳密に計算できます。ここでは、極めて単純なモデルについて、訓練誤差と汎化誤差を厳密に計算してみましょう。僕が計算が苦手で、なんどもごちゃごちゃになったので、以下の計算はうるさいくらい細かくやります。
設定
いま、何か入力$x$に対して出力$y$を観測し、入力と出力の間の関係を推定したいとしましょう。例えば、ある物質の電気抵抗を知りたいとします。入力は電圧、出力、つまり観測値は電流です。この時、入力と出力の間には線形関係
$$
y = a x
$$
が期待されます。$a$は抵抗の逆数です。しかし、観測には誤差がつきものです。いま、$n$回観測するとして、$i$番目の入力$x_i$に対して、出力$y_i$には以下のように誤差がのるとしましょう。
$$
y_i = a x_i + \varepsilon_i
$$
ただし、$\varepsilon_i$は、観測ごとに独立な平均ゼロ、分散$\sigma^2$のホワイトノイズで、以下を満たすものとします。
\begin{align}
\left[ \varepsilon_i \right]_\varepsilon &= 0 \\
\left[ \varepsilon_i \varepsilon_j \right]_\varepsilon &= \delta_{ij} \sigma^2
\end{align}
ただし、$[\cdots]_\varepsilon$はノイズに関する平均です。
さて、$n$回の観測から$a$の値を推定することを考えます。この時、訓練誤差を$E_\mathrm{training}$、汎化誤差を$E_\mathrm{test}$とすると、それぞれ
$$
E_\mathrm{training} = \sigma^2 \left( 1 - \frac{1}{n}\right)
$$
$$
E_\mathrm{test} = \sigma^2 \left( 1 + \frac{1}{n}\right)
$$
となります。まず$n=1$の時、観測点が一点しかないので、テストデータは完璧に予測できます。つまり訓練誤差はゼロです。そこから、$n$を増やしていくと、誤差が増えていって、最終的にノイズの強さでバウンドされることがわかります。
逆に、汎化誤差は、$n$が小さいほど大きく、$n$が大きいほど訓練誤差との差が小さくなって、やはりノイズの強さでバウンドされます。本稿では、これらの式を導出することを目的とします。
訓練誤差
まず、訓練誤差の導出をしましょう。そのためには訓練誤差の定義をする必要があります。訓練に使うのは$n$個のデータセット$(x_i, y_i)$の組です。ここから$y = a x$の$a$を最小二乗法で推定することにします。欲しいのは、自乗誤差
$$
C = \sum_i (y_i - \tilde{a} x_i)^2
$$
を最小にするような予測値$\tilde{a}$です。これは$\partial C/ \partial \tilde{a} = 0$となるような
$\tilde{a}$なので、
$$
\frac{\partial C}{\partial \tilde{a}} = -2 \sum_i x_i y_i + 2 \tilde{a} \sum_i x_i^2 = 0
$$
より、ただちに
$$
\tilde{a} = \frac{\sum_i x_i y_i}{\sum_i x_i^2}
$$
と求まります。ここで、後の便利のために$i$に関する算術平均を$\left<\cdots\right>$で表しましょう。つまり
$$
\left< x_i^2\right> \equiv \frac{\sum_i x_i^2}{n}
$$
です。この表記を用いると、
\tilde{a} = \frac{\left< x_i y_i \right>}{\left<x_i^2 \right>}
と表すことができます。最小二乗法の最も簡単な場合ですね。
さて、訓練誤差$E_\mathrm{training}$は、$\tilde{a}$を決めたデータセットに対する予測誤差ですから
$$
E_\mathrm{training} = \frac{1}{n} \left[ \sum_i (y_i - \tilde{a}x_i)^2 \right]_{\varepsilon,x}
$$
が定義です。ただし $\left[ \cdots\right]_{\varepsilon,x}$ は、ノイズ$\varepsilon_i$と、入力座標$x_i$のとり方に関する平均を意味します。
中の自乗をばらしてやりましょう。
\begin{align}
\frac{1}{n} \sum_i (y_i - \tilde{a}x_i)^2 &= \frac{1}{n}\sum_i y_i^2 - \frac{2 \tilde{a}}{n} \sum_i x_i y_i +\frac{1}{n} \tilde{a} \sum_i x_i^2\\
&= \frac{1}{n} \sum_i y_i^2 - 2 \tilde{a} \left< x_i y_i\right> + \tilde{a}^2 \left< x_i^2\right> \\
&= \frac{1}{n} \sum_i y_i^2 - \frac{\left<x_i y_i\right>^2}{\left<x_i^2\right>}
\end{align}
途中で先に求めた$\tilde{a}$の表式を使っています。以上から、
E_\mathrm{training} = \left[\frac{1}{n} \sum_i y_i^2 \right]_\varepsilon - \frac{\left[\left<x_i y_i\right>^2\right]_\varepsilon}{\left<x_i^2\right>}
となります。ここで、$x_i$は入力であり、入力はノイズの影響を受けないから$[\cdots]_\varepsilon$を素通りすることに注意。
この式に出てくる要素を一つ一つ評価していきましょう。まず、第一項です。
\begin{align}
\left[y_i^2\right]_\varepsilon &= \left[(ax_i+\varepsilon_i)^2 \right]_\varepsilon \\
&= a^2 x_i^2 + \sigma^2
\end{align}
ここから、
$$
\left[ \frac{1}{n} \sum_i y_i^2 \right]_\varepsilon= a^2 \left< x_i^2 \right> + \sigma^2
$$
となります。第二項は、異なるインデックスを持つノイズの積の平均がゼロであることに注意すれば、
\begin{align}
\left[ \left< x_i y_i\right>^2 \right]_\varepsilon &= \left[\frac{1}{n^2} \sum_i (a x_i^2 + \varepsilon_i) \sum_j (a x_j^2 + \varepsilon_j)\right]_\varepsilon\\
&= a^2 \left< x_i^2\right>^2 +\left[ \frac{\sum_i x_i^2 \varepsilon_i^2 }{n^2}\right]_\varepsilon \\
&= a^2 \left< x_i^2\right>^2 + \frac{\sigma^2\left< x_i^2\right> }{n}
\end{align}
と求まります。以上から訓練誤差の表式、
$$
E_\mathrm{training} = \sigma^2 \left(1 - \frac{1}{n} \right)
$$
が求まりました。なお、$\left< x_i^2\right>$がキャンセルして消えているため、入力に関する平均$[\cdots]_x$は考えなくて良いことに注意しましょう。
汎化誤差
次に汎化誤差です。いま、訓練に含まれていないデータの組$(x,y)$を新たに観測しましょう。やはりノイズが乗るので、
$$
y = ax + r
$$
となります。わかりやすさのために別記号を使いましたが、$r$は平均ゼロ、分散$\sigma^2$のホワイトノイズです。訓練用データから推定した$\tilde{a}$を使った時のテストデータの予測誤差が汎化誤差ですから、
$$
E_\mathrm{test} = \left[ (y - \tilde{a}x)^2 \right]_{r, \varepsilon, x}
$$
が汎化誤差$E_\mathrm{test}$の定義です。新たにテストデータのノイズ$r$に関する平均も取る必要があります。この$r$に関する平均は簡単に取ることができて、
\begin{align}
E_\mathrm{test} &= \left[ (y - \tilde{a}x)^2 \right]_{r, \varepsilon, x} \\
&= \left[ (ax + r - \tilde{a}x)^2 \right]_{r, \varepsilon, x} \\
&= \left[ (a-\tilde{a})x^2\right]_{\varepsilon, x} + \sigma^2 \\
&= \left[ (a-\tilde{a})\right]_{\varepsilon,x} \left[ x^2\right]_{x} + \sigma^2
\end{align}
となります。まず、$\left[ (a-\tilde{a})^2\right]_{\varepsilon}$から評価しましょう。$a^2$は定数ですから平均操作の影響を受けません。後は$a \tilde{a}$と$\tilde{a}^2$の平均操作をする必要がありますが、$\left[ \tilde{a} \right]_\varepsilon$ は簡単に評価できます。
\begin{align}
\left[ \tilde{a} \right]_\varepsilon &= \left[ \frac{\left<x_i y_i \right>}{\left< x_i ^2\right>} \right]_\varepsilon \\
&= \frac{\left[ a \left<x_i^2 \right> + x_i \varepsilon_i \right]_\varepsilon }{\left< x_i^2\right>} \\
&= a
\end{align}
$\left[ \tilde{a}^2 \right]_\varepsilon$についても、先に求めた結果を使えば、
\left[ \tilde{a}^2 \right]_\varepsilon = a^2 + \frac{\sigma^2}{n \left<x_i^2\right>}
と求まります。以上を汎化誤差$E_\mathrm{test}$の定義に代入すると、
\begin{align}
E_\mathrm{test} &= \left[ (a-\tilde{a})\right]_{\varepsilon,x} \left[ x^2\right]_{x} + \sigma^2 \\
&= \left[ a^2 - 2 a^2 + a^2 + \frac{\sigma^2}{n \left<x_i^2\right>} \right]_x \left[ x^2\right]_{x} + \sigma^2 \\
&= \frac{\left[ x^2\right]_{x}}{\left[ \left< x_i^2\right>\right]_x}\frac{\sigma^2}{n} + \sigma^2\\
&= \sigma^2 \left( 1 + \frac{1}{n}\right)
\end{align}
これが求めたい式でした。
なお、最後に
\left[x^2\right]_x = \left[ \left<x_i^2\right>\right]_x
を使っています。これは、トレーニング用とテスト用データで、入力値を同じようにサンプリングする、ということを意味しています。
まとめ
$y = a x$という線形関係がある系で、$n$個の観測値から最小二乗法を使って$a$の値を予測する問題について、訓練誤差と汎化誤差が厳密に計算できることを示しました。一つ一つの計算は全く難しくないのですが、「この場合、何が訓練誤差で何が汎化誤差なのか」「何についての平均をとっているか」がごちゃごちゃになりやすく、意外に苦戦しました。
本稿を読んだ機械学習を志す人は、是非上記を「そら」で導出できるか挑戦してください。きっとどこかで「あれ?」と混乱すると思います。なお、この計算が簡単過ぎると思った人は、$x$と$y$をベクトルにしてみたり、$y = ax + b$みたいにバイアス付きの線形関係で計算してみたりすると良いんじゃないでしょうか。
参考文献
上記の議論は、以下のレビューに出てくる例の簡単なケースです。
- A high-bias, low-variance introduction to Machine Learning for physicistsarXiv:1803.08823