1.概要
某ゲームの影響で競馬を始めて早数年。
それなりに予想法を勉強して、毎週の重賞で当たったり、外れたり。
とはいえ収支はマイナスだった。
それだけならよかったのだが、友人の誘いで地方競馬(南関東競馬)に手を出した。
友人いわく、中央競馬より簡単との事。
しかし、当たらない。中央競馬より当たらない。
収支もまあひどい。
そのような事があり、競馬AIを作ったら収支が今よりましになるのではないかと考えた。
2.機械学習モデル
競馬AIを作る上で最も重要なのは目的変数の設定だ。
着順を予想するのか、走破タイムを予想するのか。
そこで先に説明変数を考えた。
普段どのように競馬予想をしているのかといえば、馬柱と呼ばれる、出走馬の過去何走分かの結果を表にまとめたものを見ながら予想している。
ならば、説明変数にも馬柱を読み込ませればいいのでは?
そして、説明変数にその馬の過去走のデータを使うということは、その馬の能力の絶対値を計算するという事になる。
大前提として、競馬はタイムアタックではない。出走馬同士の横の比較があり、着順が決まる。そしてその着順で馬券が当たるか決まる。
ならば、その馬の絶対値を表している目的変数は何か、データに出てくる能力の絶対値のバロメーターは何か?
そう考えたときに、タイムが思いついた。
着順ならどうしても横の比較が入ってしまうが、タイムなら縦の比較のみでよいし、各馬のタイムを並べてソートすれば横の比較が可能になる。
そのため、目的変数を走破タイム、説明変数を過去5走分のデータとそのレースの施行条件とした。
データ分析、エンコーディングを行い、入力層のユニット数は269、出力層のユニット数は1とした。
また、幾つかのテストを行い、ニューラルネットワークの構造は
269→205→140→75→25→1
活性化関数は全てrelu、損失関数はMSE、最適化手法はAdam、学習率は1e-5とした。
3.学習
学習回数1000で学習を開始した。
だが、MAEが1.7を切ったタイミングで明らかにMAEの減少量が落ちている。
そこで、試しに損失関数をMAEに変えてみた。
すると、MAEの減少率が損失関数にMSEを使用したときよりも減少量が大きい。
そのため、損失関数を書き換え、MAEが1.7を切ったタイミングでMSEからMAEに切り替えるようにした。
※具体的なコードは5.付録にあります。
4.学習結果
最終的に、
MAEが訳1.02程度、MSEが1.6程度、R^2スコアが0.99程度になった。
その時の学習曲線を以下に示す。
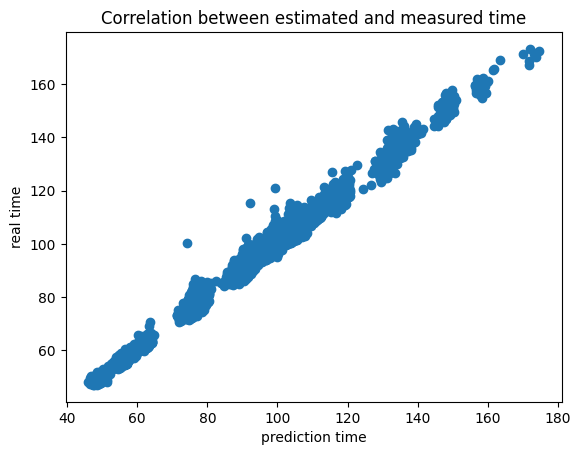
また、横軸に推定値、縦軸に正解値をとったグラフを以下に示す。
全体的にうまく推定できている。
5.実用
このモデルを使って6日ほど実際に馬券を買って検証してみた。
馬券は推定タイムが一番高い馬の単勝を買うとした。
1日目
bet:1200
return:1910
2日目
bet:1200
return:210
3日目
bet:1200
return:1760
4日目
bet:700
return:470
5日目
bet:1000
return:1580
6日目
bet:1200
return 1820
総計
bet:6500
return:7750
回収率:119.2%
6.付録
・ニューラルネットワークの定義
class Net(torch.nn.Module):
# 使用するオブジェクトを定義
def __init__(self):
super(Net, self).__init__()#親クラスのオブジェクト:Net,親クラスのメソッド:__init__():インスタンスの初期化
self.fc1 = torch.nn.Linear(269, 205)#一層から二層目までのニューラルネットワーク
self.fc2 = torch.nn.Linear(205, 140)
self.fc3 = torch.nn.Linear(140, 75)
self.fc4 = torch.nn.Linear(75, 25)
self.fc5 = torch.nn.Linear(25, 1)
# 順伝播
def forward(self, x):
x = torch.nn.functional.relu(self.fc1(x))#relu関数を活性化関数としてニューラルネットワークの結果を代入
x = torch.nn.functional.relu(self.fc2(x))
x = torch.nn.functional.relu(self.fc3(x))
x = torch.nn.functional.relu(self.fc4(x))
x = self.fc5(x)
return x
# インスタンス化
net = Net()
net
・損失関数の定義
class MixedLoss(nn.Module):
def __init__(self, a=1.7):
super(MixedLoss, self).__init__()
self.a = a
def forward(self, predictions, targets):
# 誤差を計算
errors = torch.abs(predictions - targets)
# 条件に応じて損失を選択
loss = torch.where(errors > self.a, (predictions - targets) ** 2, errors)
return torch.mean(loss)
#目的関数の設定
criterion = MixedLoss(a=1.7)#損失関数、MAEとMSEを値によって変更
criterion
・最適化手法の選択と設定
#最適化手法の選択
# net.parameters() を展開(パラメータの取得)
for parameter in iter(net.parameters()):
print(parameter)
# 初期学習率の設定
initial_lr = 1e-6
#最適化手法の設定
optimizer = torch.optim.NAdam(net.parameters(),lr=initial_lr)
optimizer
・学習ループ
net.train()
# エポックの数
max_epoch = 1000
#学習曲線用の変数
epoch_loss = []
val_epoch_loss = []
train_r2_scores = []
val_r2_scores = []
train_mae_scores = []
val_mae_scores = []
# 学習ループ(tqdmで進捗を表示)
for epoch in tqdm( range(max_epoch)):
#for batch in train:
# バッチサイズ分のサンプルを抽出
#x_tensor, t_tensor = batch
# 学習時に使用するデバイスへデータの転送
x_train_tensor = x_train_tensor.to(device)
t_train_tensor = t_train_tensor.to(device)
# パラメータの勾配を初期化
optimizer.zero_grad()
# 予測値の算出
y = net(x_train_tensor)
y_val = net(x_val_tensor)
# 目標値と予測値から目的関数の値を算出
loss = criterion(y, t_train_tensor)
loss_val = criterion(y_val,t_val_tensor)
# 目的関数の値を表示して確認
# item(): tensot.Tensor => float
#print('loss: ', loss.item())
# 各パラメータの勾配を算出
loss.backward()
# 勾配の情報を用いたパラメータの更新
optimizer.step()
#学習曲線用の変数蓄積
epoch_loss.append(loss.data.numpy().tolist())
val_epoch_loss.append(loss_val.data.numpy().tolist())
# R²スコアの計算
train_r2 = r2_score(t_train_tensor.cpu().detach().numpy(), y.cpu().detach().numpy())
val_r2 = r2_score(t_val_tensor.cpu().detach().numpy(), y_val.cpu().detach().numpy())
train_r2_scores.append(train_r2)
val_r2_scores.append(val_r2)
# MAEの計算
train_mae = mean_absolute_error(t_train_tensor.cpu().detach().numpy(), y.cpu().detach().numpy())
val_mae = mean_absolute_error(t_val_tensor.cpu().detach().numpy(), y_val.cpu().detach().numpy())
train_mae_scores.append(train_mae)
val_mae_scores.append(val_mae)
if (epoch+1) % 100 == 0:
print(f'Epoch [{epoch + 1}/{max_epoch}], Loss: {loss.item():.4f}, Val Loss: {loss_val.item():.4f}')
print(f'Train R²: {train_r2:.4f}, Val R²: {val_r2:.4f}')
print(f'Train MAE: {train_mae:.4f}, Val MAE: {val_mae:.4f}')
# 目的関数の値を表示して確認
# # item(): tensot.Tensor => float
print('loss: ', loss.item())