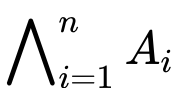自分用メモ: 論理学

TaPLを読めたり、色んな恩恵がありそうなので、論理学を学んでみる

命題論理

論理定数(又は命題定数)

"q", "r", "hoge_hoge" 等の記号

論理記号

論理記号は以下の５種類

¬ :not
(¬φ)

φ | ¬φ
- | -
1 0
0 1

∧ :and
(φ ∧ ψ)

φ ψ | φ ∧ ψ
- - | -
1 1 | 1
1 0 | 0
0 1 | 0
0 0 | 0

∨ :or
(φ ∨ ψ)

φ ψ | φ ∨ ψ
- - | -
1 1 | 1
1 0 | 0
0 1 | 0
0 0 | 0

⇒ :A then B
(φ ⇒ ψ)

φ ψ | φ ⇒ ψ
- - | -
1 1 | 1
1 0 | 0
0 1 | 1
0 0 | 1


⇔ :(A then B) and (B then A)
(φ ⇔ ψ)

φ ψ | φ ⇔ ψ
- - | -
1 1 | 1
1 0 | 0
0 1 | 0
0 0 | 1

演算子の優先順位

()で毎回くくると()が煩いので、演算子に優先順位を付ける

上が優先順位高く、下が低い

High

¬
∧
∨
⇒
⇔

Low

※1 これは http://intrologic.stanford.edu/coursera で提案された手法で、一般的かはわからない

命題語彙

命題語彙は命題定数の集合

命題言語

命題言語は、命題語彙から形成できるすべての命題文の集合

呼び方知らない演算子群

Σっぽいやつ

意味はA_1 and A_2 and ..... and A_n

出典元: https://wiis.info/math/logic/predicate-logic/inference-rule/

述語論理

述語論理は命題論理を拡張したもの。

話の世界

話の世界は有限集合でなければならない

例
話の世界: U = { a, b, c, d, e }

論理記号

論理記号は命題論理の論理記号に２つの限量記号、"全称記号 ∀"と"存在記号 ∃"が追加される

全称記号の意味は話の世界の集合の要素全てに当てはまるってことで、こんな感じ。 (詳しくは"よくわかる記号論理の159ページあたりを参照

A_1 and A_2 and ..... and A_n

束縛変項

使いそうな用語カタログ的な奴

例

∃yF(x, y)

1. 右のF(x, y)のyは∃yのyを照応している
2. 右のF(x, y)のyも∃yのyも束縛されている
   1. このように束縛されている変項を束縛変項と言う
   2. 限量記号は変項(例 x, y)と共に必ず使われる。そのため、誤解が生じない限り、変項まで含め、"∀x"や"∃y"を限量記号と呼べば、"限量記号に照応する変項は束縛されている"と言える
3. xは束縛されていないので、自由変項と言う

n項述語と変項への代入

1項述語の例
xはそそっかしい

2項述語の例
xはyが好き

このxやyの変項へ代入する方法には２通りある。
単純代入と同時代入
単純代入はxを代入してから、yを代入する
同時代入は、xとyを同時に代入する

２項述語に単純代入をした場合、１回目は１項述語になり、２回めは0項述語になる

述語言語

述語言語（Predicate Language）はPrLと呼ばれる

...やる気ある時に随時更新する