Juliaでカーブフィッティング

###この記事は?
スクリプト言語なのにC言語並の高速計算ができると評判の言語Juliaでカーブフィッティングをやってみた話です。

###パッケージ
Juliaは発展途上の言語であり、パッケージが急速に整備されています。一方でPythonなどエコシステムが出来上がった言語のようにとりあえず

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

としておけば科学技術系の計算は大体事足りる、ということはなくやりたいことに応じてパッケージを変える必要が有ります。ここがもう少し発展すれば流行ると思うのですが現状ではあまり収集がついていない印象です。

今回はプロット用のパッケージとしてPlotsを最小二乗法のパッケージとしてLinearLeastSquaresを用います。また、確率分布を扱うパッケージとしてはDistributionsを用います。なお、PlotsはバックエンドでGRを動かすと良いとの記事を見かけたのでそれにしたがっています。

###データを作る
フィッティングされる方の曲線を作ります。今回は三角関数に誤差項が乗っているデータを扱います。

using Distributions
using Plots
using LinearLeastSquares

dist = Normal(0.0, 0.05)  
eps = rand(dist, 100) 
x = collect(0.01:0.01:1.0)
f(x) = 0.5 + 0.4 * sin(2pi*x) + eps

collect()でnumpyのarange()のようなことができます。ただしarange()は後端を含めないのに対して、Juliaのcollect()は両端を含みます。記法としては、collect(start: interval: end)のようにします。

関数定義は非常に簡単にできます。また、2xのように数字を変数の前につけた場合は2*xと解釈されるので可読性が高くなります。randやsinなどの数学関数が組み込みなのはいいですね。

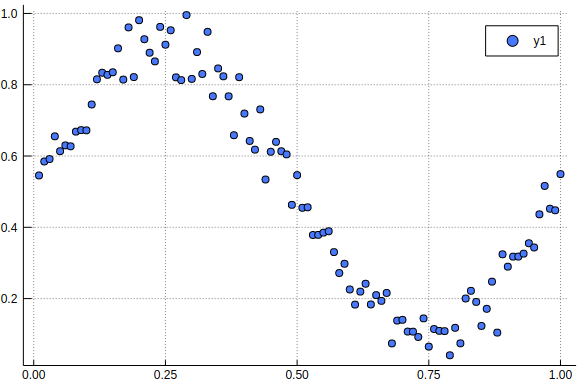
このデータを見てみます。

gr()
scatter(x, f(x))

いい感じですね。記述がシンプルでとても良いです。

###サンプル
学習用サンプルを採取します。今回は等間隔に10点とります。

index = collect(1:10:91)
x_i = x[index]
f_i = f(x)[index]

Juliaのインデックスは1始まりです。完全に罠かなんかです。MATLAB由来らしいとのことです。MATLABは個人的には使わないのですが、Juliaは結構似ていると聞きます。

###フィッティング
LinearLeastSquaresのサンプルコードに習ってフィッティングをしてみます。

slope = Variable()
offset = Variable()
line = offset + x_i * slope
residuals = line - f_i
fit_error = sum_squares(residuals)
optval = minimize!(fit_error)

シンプルですね。JuliaはRubyの影響も受けているので破壊的メソッドに!をつけるようです。他にもブロックみたいなのがあるようです。

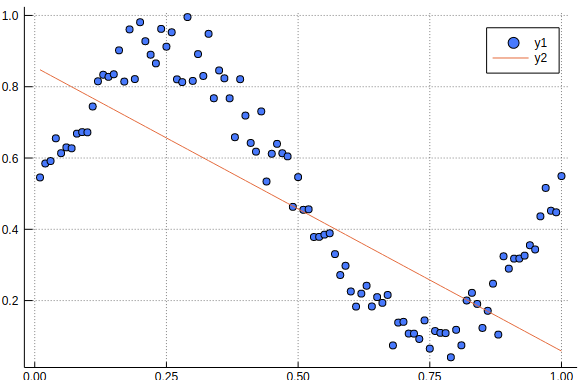
プロットしてみます。

y = evaluate(slope) * x + evaluate(offset)
plot!(x, y)

それっぽいですね。

###3次近似、6次近似、10次近似
次数を増やしてみます。任意の次数で近似できるようにしたいので関数化します。

function linear_regression(x, f, n_dims)
    offset = Variable()
    coeffs = [Variable() for i in 1:n_dims]
    
    line = offset
    for i in 1:n_dims
        line += coeffs[i] * x .^ i
    end
    
    residuals = line - f
    fit_error = sum_squares(residuals)
    optval = minimize!(fit_error)
    return offset, coeffs
end

functionキーワードでも関数定義ができます。一文で書ける関数をf(x) = ...で、ちょっと長い関数をfunctionキーワードで定義するといった使い分けなんでしょうか？ちなみに無名関数もありx -> x^2 + xみたいにかけるようです。

Juliaには内包表記があります！素晴らしいですね。

帰ってきた値からfitした曲線を作る関数も定義します。

function fitted_curve(x, offset, coeffs)
    n_dims = length(coeffs)
    line = evaluate(offset)
    for i in 1:n_dims
        line += evaluate(coeffs[i]) * x .^ i
    end
    
    return line
end

ちなみにreturn文がない場合は最後の式の評価が返り値になる？らしいです。Rubyと同じなんですかね。

定義した関数を使って見ます。

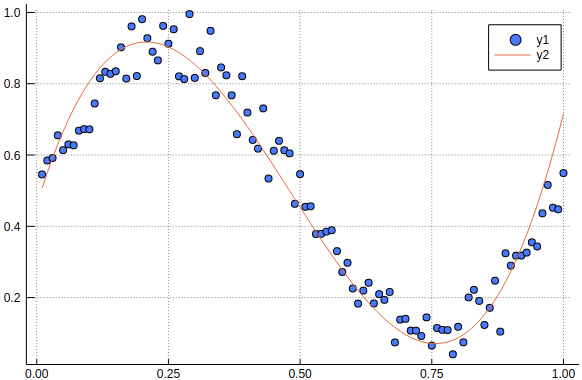
offset, coeffs = linear_regression(x_i, f_i, 3)
y = fitted_curve(x, offset, coeffs)
scatter(x, f(x))
plot!(x, y)

ちゃんと動作していますね。

offset, coeffs = linear_regression(x_i, f_i, 6)
y = fitted_curve(x, offset, coeffs)
plot!(x, y)

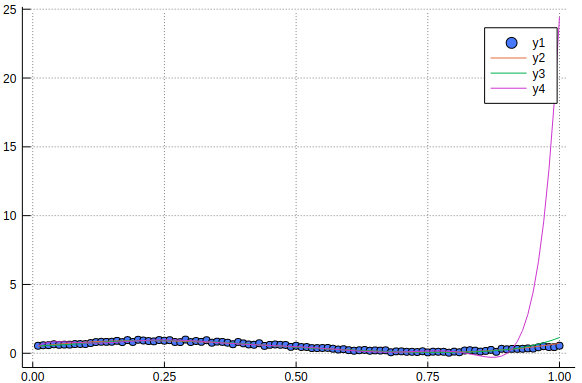
offset, coeffs = linear_regression(x_i, f_i, 10)
y = fitted_curve(x, offset, coeffs)
plot!(x, y)

十次近似を入れると見事なまでにオーバーフィッティングしてあらぬ方向に行っています。