序章
やっほー。原です。
休日にだらだら YouTube みてたら、こんな動画がおすすめに出てきたよ。

https://youtu.be/_suZM2y9wyA
最近スプラトゥーンの実況動画しか観ないから、急にこんなん出てきてびっくりしたよ。
普段観ないジャンルの動画がおすすめに出てくるとなんかポチって押しちゃうよね。
この人が言う必勝の賭け方がえれぇシンプルだったから、
「これなら簡単にシミュレーションできるやん!」
って思って、実際にやってみた。

前提
動画曰く
「ルーレットやバカラのように、当たった時の配当が 2 倍や 3 倍になるゲームにおいて有効です。」だって。
バカラってなに?
それはそうと、今回は
当たる確率が ${\frac{1}{2}}$で当たったらベット額の 2 倍ゲットできるゲームっていう前提でシミュレーションするよ。
あと、資金は無限っていう前提でやるよ。これ重要。テストに出ます。
賭け方
●準備
まず **「1, 2, 3」**という配列を用意しよう。
おわり。
●ベット金額
「ベット金額は配列の両端の数字を足したものになります。」
つまり「1, 2, 3」という配列の場合
1 + 3 = 4
だからベット金額は 4 になるよ。
※ 単位は円とかドルとかチップとか勝手に解釈していいと思うよ。
●負けた時
→ 負けた金額を数列に追加する。
4 負けた場合、
「1, 2, 3」に 4 を追加するから、数列は
「1, 2, 3, 4」になるよ。
😸<「次ベットする時は 1 + 4 = 5 になるッピ!」
●勝った時
→ 数列の両端の数字を消す。
数列が「1, 2, 3, 4」だったら、両端を消して
「2, 3」になるよ。
●終了条件
→数列が空になったら終了
数列が「2, 3」の状態で勝ったら、両端の数字を消すから数列は空になるよ。
こうなったら終わりだよ。
シミュレーションではまた数列「1, 2, 3」からやり直すことにするよ。
〜〜 賭け方の説明、おわり 〜〜
シミュレーション
さあやるぜ!!!!!!!!!!!!!!
うおおおおおおおおおおおおおおおおおおおおおあああああああああああああああああ!!
できたぜ!
小一時間ぐらいでコーディングできたよ。
いつ見ても自分のコードはきたねえ。
あ、ソースコードは下の方に載せておくよ。嫌だけどね。
●エポック数: 100000
→ 数列が空になるまでが 1 エポックとする
ってな感じで、シミュレーション開始!!!
● 1エポック目 スタート
x 負け -4 | 収支: -4
初戦敗北...
Oh my god.
● 1エポック目 スタート
x 負け -4 | 収支: -4
◯ 勝ち +10 | 収支: 1
◯ 勝ち +10 | 収支: 6
----- エポック終了 -----
あれ、終わったんだが。早いなオイ。
配列の動きとしては
「1, 2, 3」 ベット額 1 + 3 = 4
↓ 負け
「1, 2, 3, 4」 ベット額 1 + 4 = 5
↓ 勝ち
「2, 3」 ベット額 2 + 3 = 5
↓ 勝ち
「」 エポック終了
って感じだね。とりあえずちゃんと動いてるっぽいわ。良かった。
続いては 2 エポック目!!
● 2エポック目 スタート
x 負け -4 | 収支: 2
◯ 勝ち +10 | 収支: 7
◯ 勝ち +10 | 収支: 12
----- エポック終了 -----
+12 で 2 エポック目終了!!
いい感じじゃない。
それじゃあここからは 100000 エポック目まで飛ばして、結果を見よう!!!
結果発表〜〜〜〜〜〜!
:
◯ 勝ち +14 | 収支: 1089628
◯ 勝ち +12 | 収支: 1089634
----- エポック終了 -----
*************************************
- エポック数: 100000
- 合計ゲーム数: 691853
- 最終収支: 1,089,634
- 最低収支: -783,261
- 最大ベット: 389,640
*************************************
お!!
- 最終収支: 1,089,634
最終的な収支が 109 万になってる!!!
すげーーーーーーーーーーーーーーーーーーーーー
ボロ勝ちやん!!
って、ん...?
- 最低収支: -783,261
途中ぼろ負けしとるやないかーーーイ
嘘だろオイ!何があったんだってばよ!!
- 最大ベット: 389,640
39 万賭けたゲームがあったんかい!!
どんだけ大勝負に出てんだよ!
そんなん心が持たないよ!
...100000 エポックまで飛ばしてる間に色々あったんやな。
大変だったな。お疲れ様。
最終的に勝てて良かったよ。
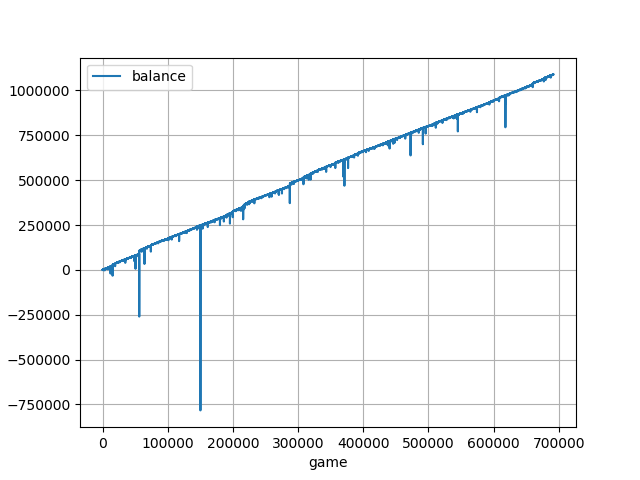
結果(プロット)
横軸がゲームで、縦軸が収支だよ。
グリッドの単位がでかいから見にくいかもしれんけど、ごめんねごめんね。
考察
他にも何回かやってみたけど、最終的な収支は必ずプラスだったよ。
しかも、やればやるほど勝ちがでかくなっていたよ。
「モンテカルロ法すげーじゃん!!」
そう思っていた時期が僕にもありました。
でも何か大事なこと忘れていませんか?
そう...
「このシミュレーションには破産という概念がない」
「資金は無限という前提でシミュレーションしている」
という落とし穴を...
やればやるほど、収支がプラスになっていくワケなんだけど、
やればやるほど、大負けする可能性も高くなっていく。
よく考えればそうよね。
負けた時、"負けた額 + α" でベットするから
連敗が続いたらベット額がえげつねーことになるよね。
「やればやるほどプラスになるが、資金が有限の場合いつか大負けして死ぬ」
死ぬのはカジノか、ギャンブラーか。
〜〜 DEAD OR ALIVE 〜〜
以上、本当は怖いモンテカルロ法でした。
おしまい。
終わりに
ここまで読んでくれた方、ありがとう。
この記事が面白いと思った方、
「いいね」 とか 「フォロー」 とか しなくて大丈夫だよ。
照れるからね。
また休日暇だったら投稿していくよ。
ソースコード
動作環境: Python 3.6.5(anaconda3-5.2.0)
大したライブラリないから anaconda なしでも動くと思うよ。
あ、その場合 matplotlib だけ pip install すれば大丈夫だと思うよ。
# -*- coding: utf-8 -*-
import random
import copy
import matplotlib.pyplot as plt
def main():
# parameter
EPOCH_NUM = 100000
MANGNIFICATION = 2 # ゲームの倍率
# const
INITIAL_BET_ARRAY = [1, 2, 3]
# balance
BALANCE = 0
# result
gameNum = 0
maxBet = 0
minBalance = 0
balanceRecordArray = []
for game in range(EPOCH_NUM):
print("● " + str(game + 1) + "エポック目 スタート")
betArray = copy.copy(INITIAL_BET_ARRAY)
while True:
gameNum += 1
bet = betArray[0] + betArray[-1]
if bet > maxBet:
maxBet = bet
BALANCE -= bet
# 勝負開始
gameResult = random.randrange(MANGNIFICATION)
if gameResult == 0: # win
BALANCE += bet * MANGNIFICATION
betArray = betArray[1:-1]
print(" ◯ 勝ち +" + str(bet * MANGNIFICATION) + " | 収支: " + str(BALANCE))
else: # lose
if BALANCE < minBalance:
minBalance = BALANCE
betArray.append(bet)
print(" x 負け -" + str(bet) + " | 収支: " + str(BALANCE))
# 記録
balanceRecordArray.append(BALANCE)
# エポック終了判定
if not betArray:
print("----- エポック終了 -----")
break
print("*************************************")
print("- エポック数: " + str(EPOCH_NUM))
print("- 合計ゲーム数: " + str(gameNum))
print("- 最終収支: " + "{:,}".format(BALANCE))
print("- 最低収支: " + "{:,}".format(minBalance))
print("- 最大ベット: " + "{:,}".format(maxBet))
print("*************************************")
plt.plot(range(len(balanceRecordArray)), balanceRecordArray, label="balance")
plt.grid()
plt.xlabel("game")
plt.ylabel("chips")
plt.legend()
plt.savefig("result.png")
if __name__ == '__main__':
main()