はじめに
こんにちは。アカツキでゲームのクライアントエンジニアをしているkackytwです。Akatsuki Advent Calender 2016でどんな話をしようかあれこれ考えた結果、会社の皆様から要望が多かった、私が趣味で作り上げたオープンソースの麻雀ゲームで採用しているAIアルゴリズムの話をしようかなと思い立ちました。ソースコードはこちらにあります。
外観
麻雀AIが扱うデータとして
- 自分の手牌データ
- 自分や相手の河牌データ
があります。
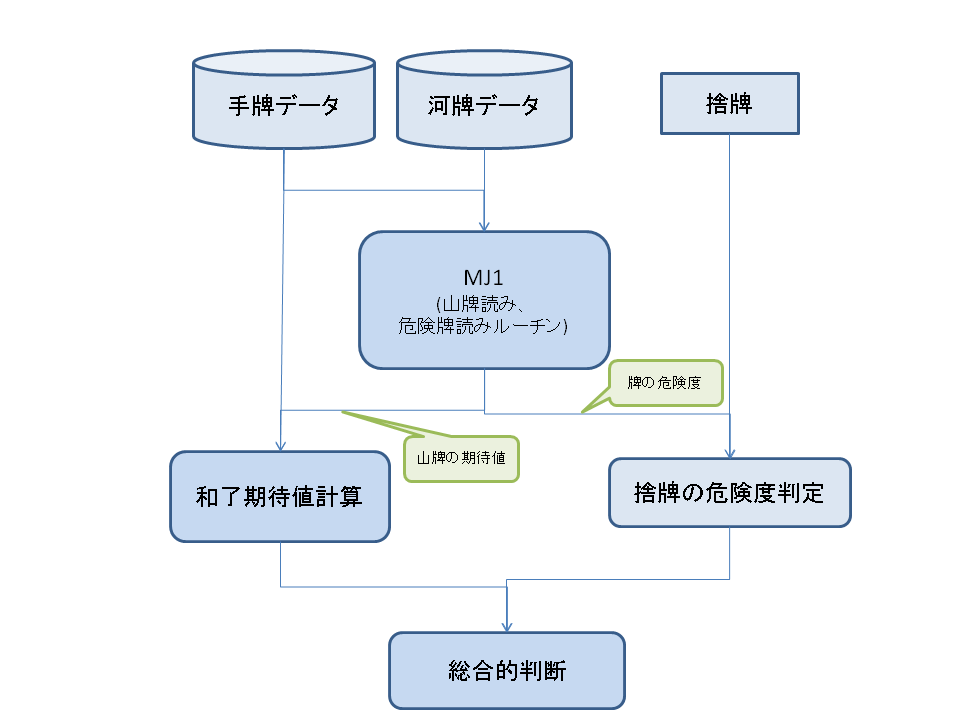
このデータに対して、私のAIでは次のようなフローを手牌の中の1つの牌を捨牌として、すべての手牌に対して行い、捨てるべき牌を決定します。
MJ1とは
とつげき東北さんの「科学する麻雀」で紹介されている、乱数を駆使した山牌、危険牌読みアルゴリズム。とつげき東北さんのサイト「システマティック麻雀工学」でもアルゴリズムの紹介がなされています。
http://totutohoku.b23.coreserver.jp/hp/mjcom.htm
サイトによれば人間の推測に匹敵、あるいはそれを上回る結果が出るそうです。書籍の方も面白いので興味のある方は手に取ってみてください。
期待値計算アルゴリズム
期待値計算アルゴリズムには様々な手法があります。私が試した方法をご紹介します。
手牌点数化方式
たとえば
- 面子 = 20
- 両面塔子 = 10
- リャンカン塔子 = 8
- 嵌張、辺張塔子 = 5
- 対子 = 8
- ドラ = 15
などといった感じに牌の組み合わせに点数を振ってこの合計が高くなるように打牌するやり方。
辺張塔子(1,2萬) = 5
面子(5萬) = 20
両面塔子(2,3筒) = 10
リャンカン塔子(5,7,9筒) = 8
で5+20+10+8=43点となる。
まうじゃんをつくっている石畑さんの本にも載ってるアルゴリズムです。
https://www.amazon.co.jp/%E3%82%B3%E3%83%B3%E3%83%94%E3%83%A5%E3%83%BC%E3%82%BF%E9%BA%BB%E9%9B%80%E3%81%AE%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82%BA%E3%83%A0-I%E3%83%BBO-BOOKS-%E7%9F%B3%E7%95%91-%E6%81%AD%E5%B9%B3/dp/4777513319/ref=asap_bc?ie=UTF8
メリット
- 非常にシンプルで理解しやすくてそこそこ和了れるAIがすぐに作れる
- 計算が速い
デメリット
- 手役を織り込みづらい(手役は1つの牌や面子ではなく、組み合わせで構成されることがある)
- 数の多い塔子 vs 面子1つなどの比較が難しい。平気で面子を落としたりする
ゲーム木構成法
ツモ牌、捨牌、ツモ牌、捨牌…でゲーム木を構成して、和了にたどり着くまで探索→期待値を計算していく方法です。
(ツモ牌=34種)×(捨牌[最大14種])で、1巡で最大476通り存在します。
メリット
- ゲームAIで一般的に採用される方法であり、それらで採用されている最適化手法を取り入れやすい
デメリット
- 愚直なやり方(総当たり)では3巡で1億通り突破して詰む\(^o^)/
- 和了までの手数が多い序盤で特につらい
- メモ化もかなりメモリーを食ってつらい
- シャンテン数によって計算量が変わるため、ユーザーにどのくらい手が進んでいるかばれてしまう
モンテカルロ法
乱数を使ってその後のツモ牌をシミュレーションし、和了した回数や点数を積算して結果がよいものを採用します。
メリット
- 役とかドラとかそのあたりの考慮を一発で織り込める
デメリット
- 計算がくそ遅い(シミュレーション回数30000回くらいやらないとものにならない)
- 七対子大好きAI(本当にそうなります。考察は今回は省きます)
和了形逆算法
手牌から和了形のすべての組み合わせへたどり着くまでの確率と上がり点を計算し、それらの積和を求めることで期待値計算を行います。1
和了形は
- チートイツ形
_{34}C_{7} = 5379616
- 平和形
順子は(1,2,3),(2,3,4),(3,4,5),(4,5,6),(5,6,7),(6,7,8),(7,8,9)の7通りで、かつ3つの色が存在するので合計21通りあり、これが4つ構成されることになるため
21^4 = 194481
- 1刻子+3順子
刻子は34通り、順子は21通りなので
34×21^3=314874
同様に
- 2刻子+2順子
_{34}C_2×21^2=247401
- 3刻子+1順子
_{34}C_3×21=125664
- 4刻子
_{34}C_4=46376
正確にはアタマがあるのでこれらに対して34倍されますが、アタマが何であるかはそれほど点数に影響することは少ない(タンヤオや一色、ドラなどはありますが)ので代表的なもの、すでに持っているものなどで計算することで計算量を削減することができます。また、チートイツ形は愚直に計算すると組合せが多すぎますが、たとえば、
- 3対子以上ない場合は計算しない(期待値ゼロ)
- 3対子以上ある場合はそれを固定した上で残りの4対子についての期待値計算を行う
などという形式にすることで組合せは
_{34}C_{4} = 46376
となり、計算量を大幅に削減することができます。計算量は大きいものの、今時のCPUを使えばなんとか現実的なアルゴリズムを実現できます。
メリット
- 計算量が巡目やシャンテン数によらず一定となる
- 役やドラを容易に織り込める
デメリット
- 計算量は多い(ゲーム木やモンテカルロほどではないが)
私は現在最後に説明した和了形逆算法を採用しています。4つのアルゴリズムを戦わせてみて現状では一番よい成績が得られたためです。どうやって戦わせているのか、ということについては今回は割愛します。
総合的判断
最後に捨牌の危険度と手牌の期待値を総合的に判断するフェーズがあります。しかし、このフェーズは実はかなり難易度が高いです。なぜなら、捨牌の危険度と手牌の期待値は同じ尺度ではないので一概に比べられないからです。今のところどうしているかといいますと、ステートマシンを使って判断を行っています。つまり、
- 上がりを目指す状態(初期状態)
- 和了期待値を採用
- オリる状態
- 牌の危険度を採用
とします。上がりを目指す状態からオリる状態へ遷移する条件としては
- 1人からリーチをかけられている => イーシャンテン以上なければオリ
- 2人以上からリーチをかけられている => テンパってなければオリ
といった感じで判断しています。オリる状態から上がりを目指す状態への遷移は採用していません。ここは賛否両論あるかと思いますが、一度オリるという意思決定をしたのであれば、それを貫き通した方が総合的にはよいのではないかと考えています。かつてはここに比較演算などをつかったファジーな判断を採用したこともあるのですが、これは判断の閾値近辺でふらふらする現象が起こります。つまり、ある巡目ではオリ、次の巡目では突っ張るといった感じで一貫性のない打牌をするということです。麻雀経験者ならわかると思いますが、これは和がれもせずに誰かに振って終わるという最悪の結果を招くことが多いです。
おわりに
ざっくりとシンプルに麻雀AIの仕組みを説明しました。それなりに理解はいただけると思いますが、ここのアルゴリズムに対して深く突っ込んでいなかったり不備はご容赦ください。また、改善の余地もたくさん残っていますのでツッコミやアイデア歓迎です^^
-
このやり方はQ学習で言うところのBellman方程式を後ろ向き推論で解くことに近しいです。https://ja.wikipedia.org/wiki/%E3%83%99%E3%83%AB%E3%83%9E%E3%83%B3%E6%96%B9%E7%A8%8B%E5%BC%8F ↩