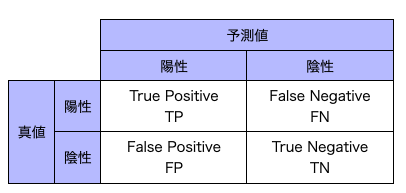
混合行列について
二値分類では混合行列を用いて予測結果を分類することができる。予測結果の「陽性;Positive」、「陰性;Negative」に対して、それが正解かどうかの「True」、「False」をつけて表現する。
- True Positive, TP:陽性と予測して、真に陽性(正解した)
- False Pisitive, FP:陽性と予測して、真には陽性ではなかった(不正解)
- True Negative, TN:陰性と予測して、真に陰性(正解した)
- False Nenegative, FN:陰性と予測して、真にいんせいではなかった(不正解)
各評価指標
Accuracy(正解率)
全データのうちどれだけ正解したかの指標。アンバランスなデータセットである場合(ex. 負例が多い)、とりあえず「負例」と答えても accuracy が 99% とかになってしまうので、データの性質に注意。
$$
\frac{TP+TN}{TP+FP+TN+FN}
$$
Precision(適合率、≒精度)
「陽性」と予測したもののうち、真に陽性であるものの割合。
$$
\frac{TP}{TP+FP}
$$
- 分母は、モデルが陽性と判断したデータ数(実際のデータの陽性数ではない)
- 分子は、正しい陽性判定数
備考点
- 分かりやすいデータにのみ(自信を持てる場合にのみ)陽性判定を行えば、FP(偽陽性)が少なくなり Precision は 100% に近くなる。
- Precision が高ければ、モデルの陽性判定は信用できることになる
- ただし、どれだけ真の陽性を見逃しているかは評価されていない。
Recall(再現率)
真に陽性であるもののうち、正しく「陽性」と予測したものの割合。
$$
\frac{TP}{TP+FN}
$$
- 分母は、真に陽性であるデータ数(実際のデータの陽性数)
- 分子は、正しい陽性判定数
備考点
- モデルがすべて「陽性」と予測した場合、FN(偽陰性)はゼロになるため Recall が100% になる
- Recall が高い場合は、真の陽性を逃していないということになる
- 「すべて陽性」と判定すると、TPも増えるがそれに伴って、FP(偽陽性)も増える
- Precision が低下するので、モデル自体の「陽性判定」に信頼が置けなくなる
Precision と Recall
Precision と Recall は以下の理由からトレードオフの関係にある。
- Precision を高くするには、FP を減らす
- 「陰性;N」判定を増やすことになり、TNと共にFNも増加する
- Recall を高くするには、FN を減らす
- 「陽性;P」判定を増やすことになり、TPと共にFPも増加する
各種指標を使いたいのは次の場合
- とにかくモデルの陽性判定が確度の高いものである必要がある場合→Precision
- ex. 広告マーケティング:DMを送付すれば効果がある、というユーザーを的確に見抜きたい。Precision が低いと、無駄なDMを大量に送付することとなってしまう
- 陽性者の見逃しを極力避けたい場合→Recall
- ex. がん患者の診断:がん患者かどうかを判定するときに、ひとまず「がんである(=陽性)」と判定しておけば、見逃しはなく多くの人命を救うことに繋がる
Specificity(特異度)
真に陰性であるもののうち、正しく「陰性」と予測したものの割合。
$$
\frac{TN}{FP+TN}
$$
F1スコア
Precision と Recall の調和平均であり、トレードオフの関係にある両者の評価指標を同時に評価し、バランスの良いモデル予測かどうかを調べることができる。
$$
F_1 = \frac{1+1}{1/P + 1/R} = 2\cdot \frac{P\cdot R}{P + R}
$$