【初心者用】主成分分析とは次元削減

目次

1.はじめに
2.主成分分析とは
3.アルゴリズム
4.コード例
5.おわりに

1. はじめに

主成分分析（Principal Component Analysis, PCA）は、多次元データを少ない次元に変換する統計的手法です。この手法は、データの特徴を保ちながら、情報を損失する最小限の次元に変換します。

今回は、機械学習やデータ解析の重要な手法であり、データの可視化や次元削減に広く使われている主成分分析について、考えてみます。

2. 主成分分析とは

例えば、英語・数学・国語・理科・社会の５つの科目の成績があるとします。数学・理科は理系科目であり、英語・国語・社会は文系科目です。
理系科目同士、文系科目同士には通常、相関がありますよね。

現在の状態では、５つの科目がそれぞれ１つの次元を占めています。つまり、５次元の空間にデータが存在しています。

主成分分析は、この５次元のデータを、新しい基底（軸）に変換します。この基底は、元の次元よりも少ない次元で、元のデータのばらつきが最大化されるように選ばれます。

例えば、２次元に削減したい場合、つまり新しい基底を２つ用意すると、データはそれぞれの基底に射影されます。この結果、元のデータを２次元の空間で表現することができます。

3. アルゴリズム

数学的には、以下の手順を踏んでいます。

1. データの標準化: 最初に、各科目の成績を標準化します。これは、データを平均が０、標準偏差が１になるように変換することです。

2. 共分散行列の計算: 次に、各科目の間の共分散を計算します。これにより、各科目間の関係性がわかります。

3. 共分散行列の固有値と固有ベクトルを計算: 共分散行列の固有値とそれに対応する固有ベクトルを計算します。固有ベクトルは新しい基底を表し、固有値はその基底の重要度を示します。

4. 上位k個の固有値に対応する固有ベクトルを選ぶ: 固有値を大きい順に並べ、上位k個の固有値に対応する固有ベクトルを選びます（kは削減後の次元数）。

5. データの射影: 選ばれた固有ベクトルを使って、元のデータを新しい基底に射影します。

これで、元の５次元のデータを２次元のデータに削減することができます。この２次元のデータは、元のデータの特徴を保ちながら、次元が削減されています。

4. コード例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

# ダミーデータ作成 (0から100の範囲に修正)
np.random.seed(0)
english_scores = np.random.randint(0, 101, 15)
math_scores = np.random.randint(0, 101, 15)
japanese_scores = np.random.randint(0, 101, 15)
science_scores = np.random.randint(0, 101, 15)
social_scores = np.random.randint(0, 101, 15)

# データを結合
scores = np.vstack((english_scores, math_scores, japanese_scores, science_scores, social_scores)).T

# 主成分分析
pca = PCA(n_components=2)
scores_pca = pca.fit_transform(scores)

# プロット
plt.figure(figsize=(8, 6))
plt.scatter(scores_pca[:, 0], scores_pca[:, 1], c='b')

# ラベル付け
for i in range(len(scores)):
    plt.text(scores_pca[i, 0], scores_pca[i, 1], f'Person {i+1}')

# ラベル設定
plt.title('PCA: Science vs Humanities')
plt.xlabel('Science Ability')
plt.ylabel('Humanities Ability')
plt.grid(True)
plt.show()

このコードでは、まず15人分のダミーテスト成績をランダムに生成し、それらをscoresとして結合しています。次に、PCAを用いて2次元に次元削減し、結果をscores_pcaに格納します。

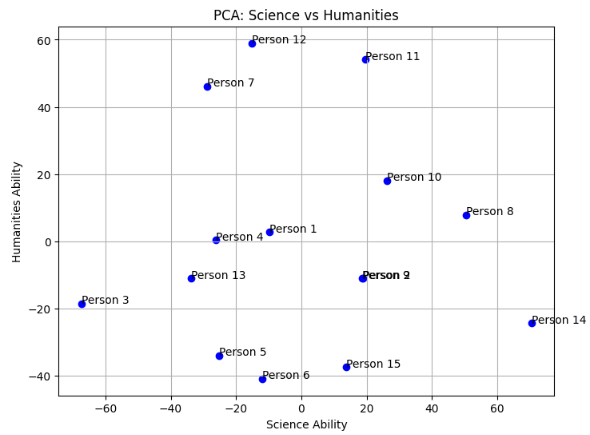
最後に、scores_pcaの2つの成分をプロットし、各点には対応するラベル（Person 1, Person 2, ...）を付けています。プロットのx軸は理科系学力、y軸は文科系学力を表します。

このコードを実行すると、PCAを用いて次元削減が行われ、2次元空間にデータがプロットされます。

結果は以下の通りです。

１．理系能力、文系能力は、英語では、それぞれ、'Science Ability'、'Humanities Ability'と言います。

２．軸の単位は、主成分分析を行った結果得られる新しい基底（軸）です。これらの基底は、元の成績データを線形変換して得られるものであり、元の成績の単位とは異なります。

通常、PCAの結果から得られる新しい軸には、元のデータの寄与度（主成分の寄与率）が付与され、その単位は特定できません。数学的には無次元の量として扱われます。

5. おわりに

いかがだったでしょうか？
もともと、英語、数学、国語、理科、社会の５科目分、５次元だったデータが、理系能力、文系能力の２次元に次元削減できました。

人は５次元を直接的には可視化できませんが、２次元であれば、簡単に可視化できますね。
ぜひ、データ分析の際、使ってみてくださいね。

主成分分析と因子分析

主成分分析（Principal Component Analysis, PCA）に似た分析手法に、因子分析（Factor Analysis）があります。

PCAはデータの主要な特徴を抽出し、次元削減に使用される一方、因子分析は観測変数の背後にある共通因子を特定し、それらの関係を理解するのに使われます。

共に、多変量解析の手法であり、データセット内のパターンや構造を理解するのに使われますが、それぞれ異なるアプローチを取ります。

1. 目的:

   • 主成分分析 (PCA): 主成分分析は、元の変数の情報をできるだけ保持しながら、データの次元を削減することを目的とします。つまり、情報損失を最小限に抑えながら、データの主要な特徴を抽出します。

   • 因子分析 (Factor Analysis): 因子分析は、観測された変数の背後にある潜在的な因子（要因）を見つけ出すことを目的とします。つまり、観測変数の変動の背後にある共通因子を特定します。

2. 仮定:

   • PCA: 主成分分析は、独立な変数を仮定します。つまり、各主成分は互いに無相関です。

   • 因子分析: 因子分析は、観測変数に共通因子と独自の因子（特有の因子）があると仮定します。共通因子は観測変数全体に影響を与え、特有の因子は個々の観測変数にのみ影響します。

3. 解釈:

   • PCA: 主成分は、元の変数の線形結合で構成されます。これらの主成分は、元の変数の情報を保持する新しい基底を表します。

   • 因子分析: 共通因子は、観測変数の変動に影響を与える要因を表します。特有の因子は、観測変数固有の要因を表します。

4. 適用例:

   • PCA: PCAは、次元削減やデータの可視化に使われます。例えば、顔の画像データを2次元に圧縮して顔の特徴を可視化する場合など。

   • 因子分析: 因子分析は、心理学や社会科学などで使われ、観測された変数の背後にある潜在的な因子（例: 性格特性、能力など）を探索するのに使われます。