目次
1.構造方程式モデリングとは
2.準備
3.分析
4.仮説
5.学習
6.おわりに
1. 構造方程式モデリングとは
構造方程式モデリング(Structural Equation Modeling, SEM)は、統計学の手法の一種であり、複数の変数間の関係を同時に評価するために用いられる強力なツールです。
SEMは、観測変数(測定された変数)と潜在変数(観測できないが仮想的に存在する変数)の間の関係をモデル化することができます。これにより、複雑な現象やシステムを統計的に理解しやすくなります。
以下にSEMの主な要素を説明します。
-
構造モデル
- SEMでは、潜在変数と観測変数の間の関係を表現する数学的なモデルがあります。これは通常、線形方程式や因果関係のモデルとして表現されます。
-
観測モデル
- 観測変数は、実際にデータとして得られる変数です。SEMでは、観測変数が潜在変数をどの程度正確に反映しているかを示す観測モデルがあります。
-
潜在変数
- 潜在変数は、直接観測することができないが、理論的に重要な概念や特性を表します。例えば、幸福度や知識などが潜在変数の例です。
-
パス
- パスは、変数間の直接的な影響や関係を示します。例えば、AがBに影響を与える場合、AからBへのパスが存在します。
-
誤差項
- 観測変数や潜在変数の値がモデルから予測される値と実際の値のズレを示す誤差項があります。
SEMの利点は、複数の変数間の複雑な関係を同時に扱えることです。例えば、教育の影響を調査する場合、学力、学習環境、家族の影響などの要因が相互に影響し合う場合、SEMはそれらの関係を包括的にモデル化できます。
SEMは社会科学、心理学、経済学、教育学など幅広い分野で利用されており、研究者や分析者にとって重要なツールとなっています。
2. 準備
それでは、具体的に構造方程式を使っていきましょう。
まず、必要なライブラリやモジュールの準備をしましょう。
#共分散構造分析を行うためのライブラリ
!pip install semopy
#パス図を出力するためのライブラリ
!pip install graphviz
#モジュールのインポート
import pandas as pd
import seaborn as sns
import semopy
from semopy import Model
from sklearn import datasets
今回は、データはscikit-learnが提供しているリネルドのデータを使用します。
Linnerud データセットは、20 人の成人男性がフィットネスクラブで測定した 3 つの生理学的特徴(体重、胴囲、脈拍)と、3つの運動能力(懸垂の回数、腹筋の回数、跳躍)の関係を示したデータセットです。
「体重」「胴囲」「脈拍」と、「懸垂の回数」「腹筋の回数」「跳躍」の関係がデータとして提供されています。
#データセット
df = datasets.load_linnerud(as_frame=True).frame
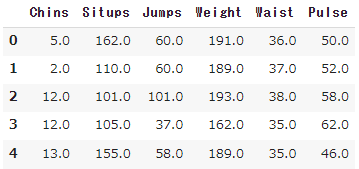
df.head()
データは、こんな感じです。
各変数の単位による影響をなくすためのデータの標準化(平均 0、分散 1)を行います。
#データの標準化
df_std = df.apply(lambda x: (x-x.mean())/x.std(), axis=0)
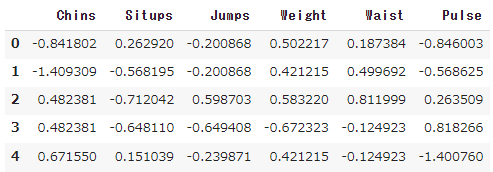
df_std.head()
3. 分析
仮説を考えるため、まず、各変数の相関を見てみましょう。
df_std_corr = df_std.corr()
df_std_corr
相関は、以下の通りです。
ヒートマップにした方が分かりやすいので、ヒートマップにします。
sns.heatmap(df_std_corr, cmap="coolwarm", vmin=-1, vmax=1, annot=True)
ヒートマップは、以下の通りです。カラーマップは分かりやすいですね。
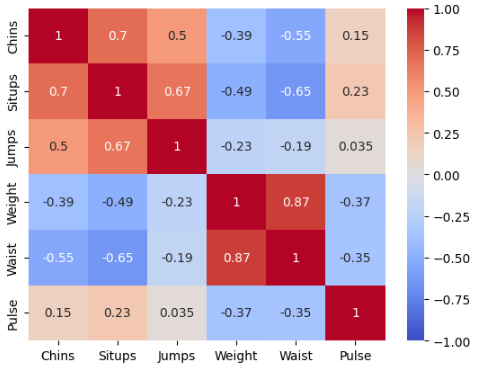
ヒートマップからは、以下のことが分かります。
1.「懸垂の回数」「腹筋の回数」「跳躍」は、それぞれ、相関が高い。
2.「体重」と「胴囲」は、相関が高い。
3.「脈拍」は、他の要素と、あまり相関が見られない。
4. 仮説
相関を考慮して、仮説を考えます。ここでは、以下の仮説を立てます。
1.「懸垂の回数」「腹筋の回数」「跳躍」の裏には、身体能力という潜在変数があるとします。
2.「体重」と「胴囲」の裏には、身体という潜在変数があるとします。
3.「懸垂の回数」「腹筋の回数」「跳躍」は、それぞれ、身体能力と身体により説明されるものとします。
4.「懸垂の回数」「腹筋の回数」「跳躍」は、それぞれ、相互に共変関係があり、「体重」と「胴囲」の間にも共変関係がある。
次に、仮説モデルを変数descに代入します。
仮説において、構造方程式を使用しますので、構造方程式モデリングと言います。
# 仮説モデルを変数descに代入する
desc = '''
# 測定方程式(潜在変数 =~ 観測変数)
Capability =~ Jumps + Situps + Chins
Body =~ Waist + Weight
# 構造方程式(目的変数 ~ 説明変数、潜在or観測どちらもOK)
Chins ~ Capability + Body
Situps ~Capability + Body
Jumps ~ Capability + Body
# 共変関係(双方向、潜在or観測どちらもOK)
Chins ~~ Situps
Situps ~~ Jumps
Chins ~~ Jumps
Weight ~~ Waist
'''
5. 学習
いよいよ、構造方程式モデリングを使った、学習を行います。
semopyのModelを用意して、fitで学習させ、inspectで学習結果のパラメータ一覧を表示することができます。
# 学習器を用意
mod = Model(desc)
# 学習結果をresに代入する
res = mod.fit(df_std)
# 学習結果のパラメータ一覧を表示する
inspect = mod.inspect()
print(inspect)
学習結果のパラメータ一覧は、以下の通りです。
モデルの評価をしてみましょう。
# モデルの評価指標を表示
stats = semopy.calc_stats(mod)
# 転置して表示
print(stats.T)
注目したいのがCFI、GFI、AGFI、NFIの4つ。
これらはモデルの適合度指標と呼ばれ、0.9以上であれば良いモデルと言えます。
まずまずの適合度ですね。
グラフ化は、以下のコードで行います。
pass_graph = semopy.semplot(mod, "sample.png", plot_covs=True, engine="dot")
pass_graph
グラフ化した結果は、以下の通りです。
6. おわりに
構造方程式モデリング、如何だったでしょうか。
観測変数の裏に潜む、潜在変数を図示出来るのは、とても、面白かったです。
もちろん、仮説を立てるところが大切ですので、分析者の腕の見せ所かもしれません。
因子分析を高度にした分析として、いろんなところで、活用できると良いですね。