目次
1.はじめに
2.平均
3.分散
4.標準偏差
5.おわりに
1. はじめに
1.平均はデータの大雑把な状況を把握する代表値の主役です。
2.分散が分かると、個々のデータの大雑把な立ち位置が分かります。
3.標準偏差から偏差値が求められます。
2. 平均
もし、試験の結果が60点だったとして、これって、良かったのか、悪かったのか、分からない。でも、平均が40点だったとした、60点は悪くない。逆に、平均が80点だったとしたら、60点は平均以下ということで、イマイチの結果だった、ということ。
つまり、全体の大雑把な傾向を把握するのに、平均は便利。
平均(Mean):
$$
\text{平均} = \frac{1}{n} \sum_{i=1}^{n} x_i
$$
ここで、n はデータの個数で、$x_i$はデータの値(i番目のデータ)です。
import numpy as np
# ダミーデータ
data = [12, 15, 18, 20, 22, 25]
# 平均の計算
mean = np.mean(data)
print("平均:", mean)
結果は、平均: 18.6となります。
代表値
全体的な傾向を把握する数値は代表値(Descriptive StatisticsまたはSummary Statistics)と言います。データセットの特徴を要約し、理解するために使用される数値です。以下に代表的な代表値とその有用な場面を簡単に説明します。
平均(平均値、Mean):数値データ全体の中心的な値を知りたい場合に使用されます。例えば、テストの平均点や商品の平均価格などです。
ちなみに、英語のAverage は一般的な意味での平均で、代表値を意味するときもあります。統計などの専門的な話をするときには Mean を使うと良いですね。
中央値(Median):データを昇順または降順に並べたときに、ちょうど中央に位置する値です。データセットに外れ値(極端な値)が含まれる場合や、データの分布が歪んでいる場合に、平均よりも代表的な中心値を求めるために使用されます。所得なんかは、とても大きい人がいるので、中央値を使うのが良いですね。
最頻値(Mode):データセット内で最も頻繁に現れる値です。
カテゴリカルなデータ(例: 色やカテゴリなど)において、最も一般的な選択肢を知りたい場合に使用されます。例えば、アンケートの回答の中で最も多い回答などです。
なお、平均は全体的な傾向を把握する上で、とても大切だけど、一つ一つのデータの個性みたいなものは、捨象した概念だから、その点は、頭の片隅に置いておいてください。
3. 分散
平均と比べることで、自分が全体の真ん中より上か下か、分布をグラフ化したときに山の右か左かは、分かるようになりました。
でも、どれくらい、平均より良いのかは分からない。もちろん、平均との差の絶対値の大きさも大切だね。でも、例えば、試験の例で言うと、平均点付近に、みんなの成績が集まっている試験がある一方、点がバラけている試験もある。
そのバラけ具合を判断するのが、分散です。分散は平均との差の二乗を足して、データの数で割ったものです。平均との差は、プラスの場合も、マイナスの場合もあるので、二乗して、正の数にしています。
試験の点数がバラけている場合、分散は大きくなるし、逆に、みんなの点数が平均点の周辺に集まっている場合、分散は小さくなります。
分散(Variance):
$$
\text{分散} = \frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2
$$
ここで、$\mu$は平均です。
# 分散の計算
variance = np.var(data)
print("分散:", variance)
結果は、分散: 18.5となります。
共分散
分散と似た用語で、共分散(Covariance)があります。統計学において2つの異なる変数がどれだけ同時に変動するかを測るための指標です。1つの変数が増加するときに他の変数も増加するか、減少するかを示します。共分散は、変数間の関連性や相関性を理解するのに役立ちます。
4. 標準偏差
分散は、平均との差の二乗の平均をとった数値なので、平均と足したり引いたりすると変なことになる。そこで、分散の平方根をとって、平均と次数をそろえることで、足したり引いたりできるようにしたのが、標準偏差です。
標準偏差(Standard Deviation):
$$
\text{標準偏差} = \sqrt{\text{分散}} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2}
$$
# 標準偏差の計算
std_deviation = np.std(data)
print("標準偏差:", std_deviation)
結果は、標準偏差: 4.3となります。
5. おわりに
平均と分散と標準偏差のうち、標準偏差は分散の平方根ですから、平均と標準偏差の2つが分かると、データの形状が分かります。
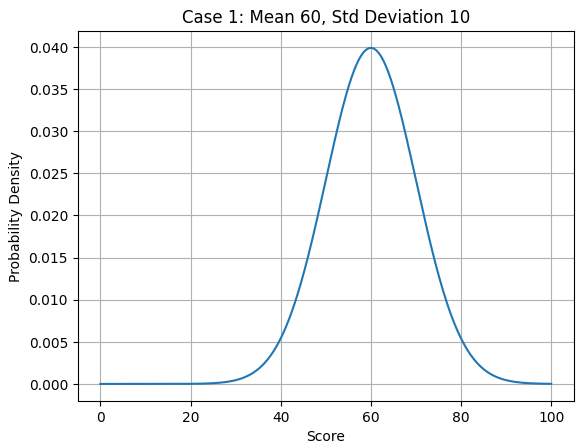
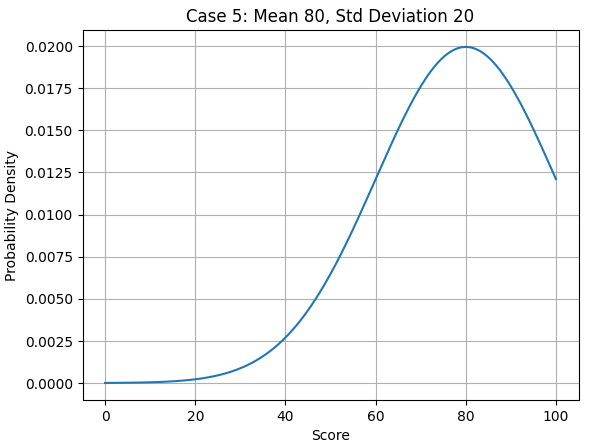
最後に、平均と標準偏差を基に、いくつか、グラフを載せておきます。見ていただくと、なんとなく、イメージが湧くと思います。
ケース1:平均60点、標準偏差10点
ケース2:平均40点、標準偏差5点
ケース3:平均40点、標準偏差20点
ケース4:平均80点、標準偏差5点
ケース5:平均80点、標準偏差20点
参考までに、ケース1のコードを載せておきます。平均と標準偏差を変更すれば、他のケースのコードになります。
import matplotlib.pyplot as plt
import numpy as np
mean1 = 60
std_deviation1 = 10
x1 = np.linspace(0, 100, 500)
y1 = (1/(std_deviation1 * np.sqrt(2*np.pi))) * np.exp(-0.5*((x1 - mean1)/std_deviation1)**2)
plt.plot(x1, y1)
plt.title('Case 1: Mean 60, Std Deviation 10')
plt.xlabel('Score')
plt.ylabel('Probability Density')
plt.grid()
plt.show()