LoginSignup
1
4
@ka201504

因子分析とは何か？主成分分析との比較

Last updated at Posted at 2023-10-15

目次

1.はじめに
2.分析のアプローチ
3.分析のモデル
4.Pythonでの実装
5.おわりに

1. はじめに

因子分析って、個人的には、ちょっと、分かりにくいです。
主成分分析との違いも、分かりにくいです。
因子分析とは、一体、何なのか？　
主成分分析と比較した上で、調べてみましたので、共有させて頂きます。
Pythonを使った、コードも載せましたので、ご覧ください。

2. 分析のアプローチ

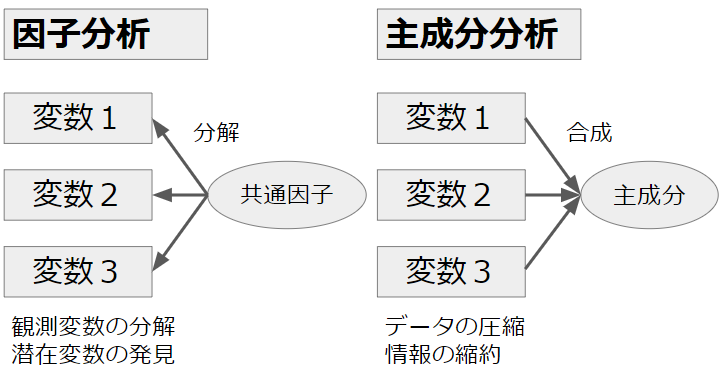
因子分析は、共通因子の働きを各変数について分解し、観測変数の背後にある潜在変数として、見つけ出します。
一方、主成分分析は、各変数を主成分に合成し、データの圧縮、情報の縮約を行います。

image.png

因子分析と主成分分析は、多変量データを理解しやすくするための統計的手法です。
それぞれのアプローチは、データ解釈のために異なる観点からアプローチします。

  1. 因子分析

    • 背景

      • 因子分析は、観測変数（例: アンケートの質問項目）の背後に存在する潜在的な要因や因子を明らかにするための手法です。つまり、観測できないが重要な影響を与える要因を見つけ出します。
      • 例えば、人々の健康に影響を与える要因は、遺伝、環境、生活習慣などがありますが、これらは直接観測できないですよね。因子分析は、このような隠れた要因を理解しようとします。

    • アプローチ

      • 観測変数同士の相関を解析し、それらの背後にある共通因子を特定します。例えば、健康に関連するアンケート項目（食事、運動、ストレスなど）が相関する場合、それらは共通の「健康」因子に起因する可能性があります。

    • 目的

      • 様々な観測変数を効果的に要約し、データの潜在的な構造や関係を明らかにすることです。

  2. 主成分分析

    • 背景

      • 主成分分析は、元のデータをより少ない変数（主成分）に圧縮する手法です。これによって、データの情報をできるだけ保持しながら次元を削減します。

    • アプローチ

      • 変数間の相関を利用して、データを新しい軸（主成分）に射影します。最初の主成分は最もデータのばらつきを説明する軸であり、次の主成分はそれに直交する軸で、次に多くのばらつきを説明します。
      • つまり、分散の最大化です。

    • 目的

      • 元のデータの情報を保持しながら、次元を減らし、データを簡潔に理解しやすくします。主成分は元の変数と異なる軸上に位置するため、元の変数の意味を持たない場合もあります。

因子分析と主成分分析の違い

まとめると、因子分析は隠れた構造や因子を見つけるために使われ、観測変数を潜在的な共通要因に分解します。一方、主成分分析はデータの情報を最大限保持しながら次元を削減し、データを簡潔に表現します。

例えば、健康調査を考えてみましょう。因子分析では、食事、運動、ストレスなどの観測変数を分解して、共通の健康因子を見つけ出します。主成分分析では、これらの健康関連の変数を組み合わせて、新しい指標を作成し、それを用いて健康状態を説明します。

どちらの手法もデータ解釈を容易にし、異なる観点からデータを理解するのに役立ちます。しかし、それぞれのアプローチが異なる側面に焦点を当てています。

3. 分析のモデル

因子分析は、共通因子に加え、観測変数ごとの独自因子を考えます。
一方、主成分分析は、主成分を考えるだけで、独自因子のようなものは、考えません。

因子分析では、独自因子を考えるため、変数が条件式より多いので、分析結果が数学的に厳密には一義には決まりません。また、因子の数によって、分析結果も異なります。

一方、主成分分析では、独自因子のようなものを考えないため、変数と条件式が同一で、固有値問題を解くことで、分析結果が一義に決まります。

image.png

因子分析と主成分分析のモデルの違いについて、考えます。

因子分析:

因子分析の基本モデルは以下の通りです。

  1. 観測モデル

観測変数 $X$ と共通因子 $F$ 、および独自因子 $U$の関係を表します。

X = \Lambda F + U
  • $X$ : 観測変数の行列 (n×p)
  • $\Lambda$ : 因子負荷行列 (p×m) - (m) は共通因子の数
  • $F$ : 共通因子の行列 (n×m)
  • $U$ : 独自因子の行列 (n×p)

このモデルでは、共通因子 $F$ と独自因子 $U$ の影響が考慮されます。

  1. 分散共分散行列

    観測変数の分散共分散行列は以下のように表されます。

    $$\Sigma = \Lambda \Lambda' + \Psi $$

    • $\Sigma$ : 観測変数の分散共分散行列 (p×p)
    • $\Lambda'$ : $\Lambda$ の転置
    • $\Psi$ : 独自因子の分散共分散行列 (p×p)

なお、観測変数の分散共分散行列は、標準化（平均を０、分散を１にする）していれば、相関行列と同じになります。
このため、相関行列を標準化したのち、分散共分散行列として、計算に用います。

主成分分析

主成分分析の基本モデルは以下の通りです。

  1. 観測モデル

    主成分 $Z$ と主成分負荷行列 $L$ の関係を表します。

    $$Z = XL$$

    • $Z$ : 主成分の行列 (n×m) - $m$ は主成分の数
    • $L$ : 主成分負荷行列 (p×m)

    このモデルでは、主成分 $Z$ のみが考慮されます。

  2. 分散共分散行列

    主成分の分散共分散行列は以下のように表されます。

    $$\Sigma_Z = LL' $$

    • $\Sigma_Z$ : 主成分の分散共分散行列 (m×m)

違いの解説

  1. 因子分析

    • モデルには共通因子 $F$ と独自因子 $U$ が含まれます。
    • 因子数 $m$ を変えると、解が異なる可能性があります。
    • 分散共分散行列は共通因子の影響と独自因子の影響を反映します。

  2. 主成分分析

    • モデルには主成分 $Z$ のみが含まれます。
    • 固有値問題の解によって主成分が一義的に決まります。
    • 分散共分散行列は主成分の影響のみを反映します。

因子分析では共通因子と独自因子の影響を考慮し、主成分分析では主成分のみが考慮されるため、モデルの構造や解釈が異なります。また、因子分析では因子数の選択が重要であり、主成分分析ではこのような選択はありません。

4. Pythonでの実装

それでは、いよいよ、Pythonで、実装してみましょう。

(1)因子分析のコード

A.準備

まず、準備として、必要なライブラリやデータの準備をしましょう。
今回は、主要５科目について、２０人分のダミーデータを使います。

import pandas as pd
from factor_analyzer import FactorAnalyzer
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns

# データの準備
data = {
    'No': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20],
    '英語': [60, 42, 66, 81, 74, 60, 55, 53, 78, 49, 88, 38, 50, 43, 66, 43, 75, 52, 58, 46],
    '数学': [86, 30, 45, 85, 77, 67, 52, 46, 48, 40, 80, 41, 25, 34, 29, 52, 38, 71, 65, 28],
    '国語': [51, 54, 49, 73, 63, 50, 42, 57, 81, 66, 72, 57, 44, 29, 66, 51, 73, 69, 35, 42],
    '理科': [72, 31, 61, 95, 36, 41, 71, 55, 47, 45, 56, 25, 38, 24, 37, 72, 40, 63, 50, 29],
    '社会': [41, 46, 62, 77, 65, 53, 38, 52, 78, 63, 71, 50, 60, 38, 73, 65, 81, 70, 66, 44]
}

B.データの確認

df = pd.DataFrame(data)
df.head()

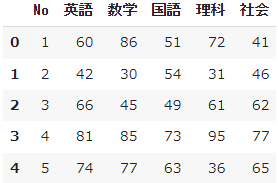
データは、こんな風になっています。

image.png

No.は、後ほど、主成分分析で、データのプロットをする際に、利用します。

C.相関行列

相関係数を一覧化した相関行列を求めます。

# 相関行列を計算
corr_matrix = df.iloc[:, 1:].corr()

# 相関行列を可視化
plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', xticklabels=df.columns[1:], yticklabels=df.columns[1:])
plt.title("相関行列")
plt.show()

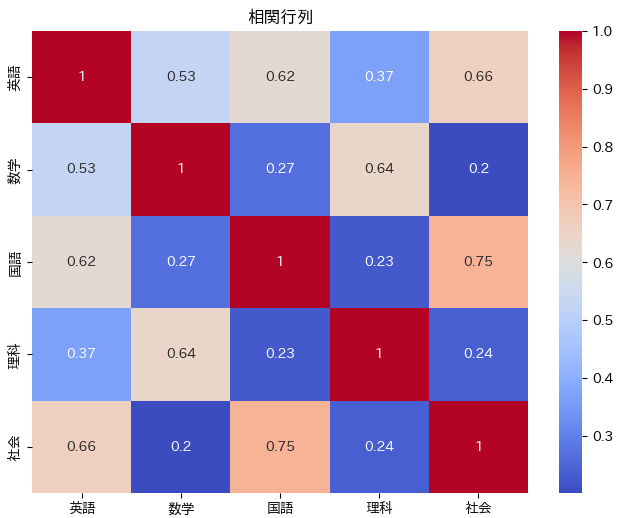
相関行列は、以下の通りです。
「英語は、国語、社会と」、「数学は、理科と」、相関関係が見て取れます。

image.png

D.因子分析と因子負荷行列

次に、因子分析をして、因子負荷行列を求めます。

# 因子分析
# 因子数を2に指定
fa = FactorAnalyzer(n_factors=2, rotation=None)
fa.fit(df.iloc[:, 1:])

# 因子負荷行列をデータフレームとして取得
factor_loadings = pd.DataFrame(fa.loadings_, columns=[f'Factor{i+1}' for i in range(2)], index=df.columns[1:])

# 因子負荷行列を表示
print("因子負荷行列:")
print(factor_loadings)

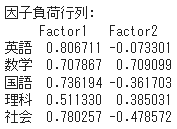
因子負荷行列は、以下の通りです。

image.png

第一因子は、すべての教科で、プラスですね。これは「総合学力」を示しています。
一方、第二因子は、数学と理科で、プラスですね。これは「理系学力」を示しているということです。

E.因子数の検証

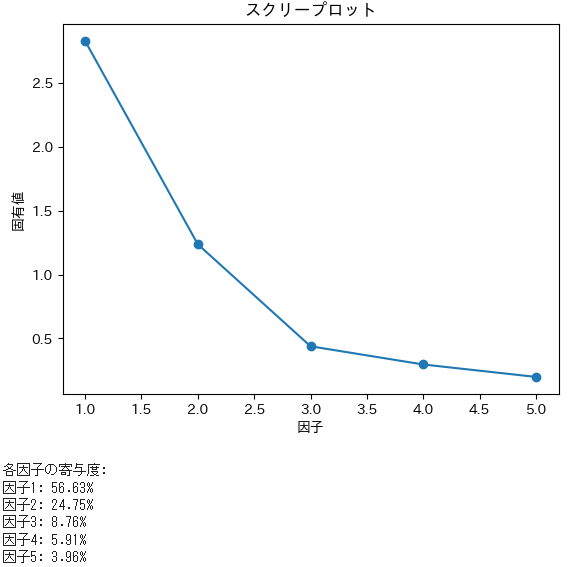
今回、因子を２つにしましたが、本当に２つで良かったのか、スクリープロットを表示し、各因子の寄与度も求めてみます。

# スクリープロットを表示
ev, v = fa.get_eigenvalues()
plt.plot(range(1, len(ev)+1), ev, marker='o')
plt.title("スクリープロット")
plt.xlabel("因子")
plt.ylabel("固有値")
plt.show()

# 各因子の寄与度を計算
total_variance = np.sum(ev)
variance_explained = (ev / total_variance) * 100
print("\n各因子の寄与度:")
for i, var in enumerate(variance_explained):
    print(f"因子{i+1}: {var:.2f}%")

image.png

スクリープロットでは、因子２つ目までが、固有値１を超えています。
また、因子の寄与度を見ると、上位２つの因子で、８割となっています。
因子の数は、２つで良かったようです。

主成分分析のコード

主成分分析は、今回の本題ではないので、コードのみ、全文、記載しておきます。
３つのグループ分けをしていますが、そのグループの意味もコードにコメントしてあります。

import pandas as pd
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import japanize_matplotlib

# データの準備
data = {
    'No': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20],
    '英語': [60, 42, 66, 81, 74, 60, 55, 53, 78, 49, 88, 38, 50, 43, 66, 43, 75, 52, 58, 46],
    '数学': [86, 30, 45, 85, 77, 67, 52, 46, 48, 40, 80, 41, 25, 34, 29, 52, 38, 71, 65, 28],
    '国語': [51, 54, 49, 73, 63, 50, 42, 57, 81, 66, 72, 57, 44, 29, 66, 51, 73, 69, 35, 42],
    '理科': [72, 31, 61, 95, 36, 41, 71, 55, 47, 45, 56, 25, 38, 24, 37, 72, 40, 63, 50, 29],
    '社会': [41, 46, 62, 77, 65, 53, 38, 52, 78, 63, 71, 50, 60, 38, 73, 65, 81, 70, 66, 44]
}

df = pd.DataFrame(data)

# 主成分分析の実施
pca = PCA()
principal_components = pca.fit_transform(df.iloc[:, 1:])

# 主成分得点をDataFrameに変換
pc_df = pd.DataFrame(data=principal_components, columns=[f'PC{i+1}' for i in range(len(df.columns)-1)])

# 寄与率と累積寄与率を計算
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_explained_variance = explained_variance_ratio.cumsum()

# 主成分負荷量を取得
loadings = pca.components_

# 結果の表示
print("各主成分の寄与率:")
for i, ev in enumerate(explained_variance_ratio):
    print(f"PC{i+1}: {ev:.4f}")

print("\n各主成分の累積寄与率:")
for i, cev in enumerate(cumulative_explained_variance):
    print(f"PC{i+1}: {cev:.4f}")

# 主成分得点のプロット
plt.figure(figsize=(8, 6))

# 各グループの主成分得点の散布図を描画
# Group 1: 英語と数学が高め
plt.scatter(pc_df['PC1'][:10], pc_df['PC2'][:10], color='blue', label='Group 1')
# Group 2: 国語と社会が高め
plt.scatter(pc_df['PC1'][10:15], pc_df['PC2'][10:15], color='red', label='Group 2')
# Group 3: 理科が特に高め
plt.scatter(pc_df['PC1'][15:], pc_df['PC2'][15:], color='green', label='Group 3')

# 主成分ごとの補助線を引く
plt.axhline(0, color='black', linestyle='--', alpha=0.5)
plt.axvline(0, color='black', linestyle='--', alpha=0.5)

# ラベルの表示（大きくする）
for i, txt in enumerate(df['No']):
    plt.annotate(txt, (pc_df['PC1'][i], pc_df['PC2'][i]), fontsize=15, ha='right')

plt.title('主成分得点')
plt.xlabel('第1主成分')
plt.ylabel('第2主成分')
plt.legend()
plt.show()

# 主成分負荷量の表示
loadings_df = pd.DataFrame(loadings, columns=df.columns[1:], index=[f'PC{i+1}' for i in range(len(df.columns)-1)])
print("\n主成分負荷量:")
loadings_df

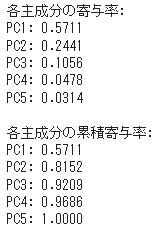
出力結果は、以下の通りです。

image.png

寄与率は、主成分１と主成分２の合計で、８割となっています。

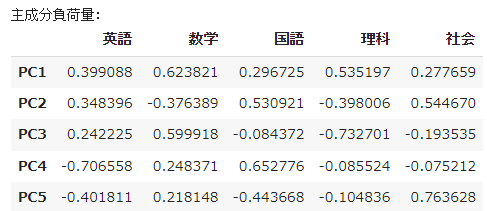
image.png

主成分負荷量は、主成分１が、因子分析と同様、「総合学力」ですが、主成分２は、因子分析では「理系学力」だったものが、主成分分析では「文系学力」となっているようです。
まあ、実質的には変わりはないのかもしれません。

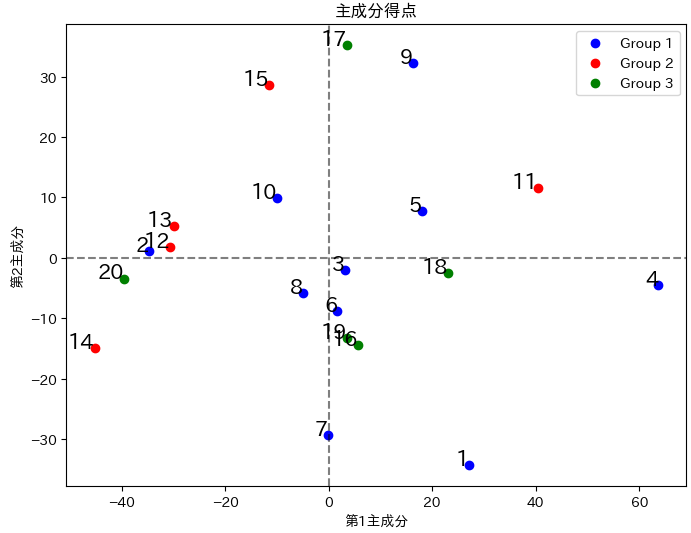
グループ分けした散布図も参考までに載せておきます。
グループの意味は、以下の通りです。
Group 1: 英語と数学が高め
Group 2: 国語と社会が高め
Group 3: 理科が特に高め
image.png

5. おわりに

因子分析と主成分分析、似て非なるもの、という感じです。
今回、調べてみて、似ている部分と異なる部分が、よく分かりました。

もし、間違った個所などがあれば、お気軽に、ぜひ、教えてください。

因子分析を上手に活用して、アンケートの分析など、やってみたいです(笑)

1
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
4