スパコンのベンチマークについて

　シングルヘル……シングルヘル……

令和2年12月24日木曜日、皆様いかがお過ごしでしょうか？
お仕事ですか？自粛ですか？

　シングルヘル……誰が為に鈴は鳴る……

真面目な技術記事も有益なのですがもう少しポエムっぽく行きましょう。

　Single Hell... Single Hell... Stay Home alone.

本日は@k_nitadoriがスパコン「富岳」で2期連続4冠となったベチマークについて思うところを書こうと思います。

（※）個人の見解であり所属機関とは一切関係ありません

散々がいしゅつ（→既出 <もしかして:きしゅつ>）な話題なのですが、あくまでもポエムなので語り部によって異なる趣をお楽しみください。

---

突然の宣伝になってしまうのですが、筆者はHPC-Physなる勉強会の世話人というをやっています。特にオンライン開催の第8回及び第9回では「富岳」におけるベンチマーク特集というのをやらせていただきました。HPCG以外はこちらの資料も交えた叙事詩を紡ぎ出せればと思います。

こういう勉強会、一度始めてしまうと枠を埋めるのに奔走し続けなくてはならないのが辛いところです。

　シングルヘル！

#HPL

HPLはHigh Performance LINPACKのこと。LINPACKは元々はライブラリの名前だったのですが、そこからスピンオフしたLINPACKベンチマークの方が有名になりました。HPLは並列計算機向けに並列化されたLINPACKベンチマークとなります。
スパコン（≒並列計算機、今日でほぼ同じ）のベンチマークとしては、あからさまにバラバラに計算できるもの（実用上は大事だけど）は不適格、逆にどうやっても並列化できなさそうなもの（これも大事だったりするけれど）も不適格ということで巨大な線形方程式の解法（並列化できるけど1台では解ききれない）が採用されたのかもしれません。
ここで富士通竹重さんの資料を見てみましょう。HPLで一番内側の処理となる倍精度の行列行列積の DGEMM （単精度や半精度の SGEMM や HGEMM も）の実装について詳細な説明があります。HPLを行うにあたっては先ずは DGEMM でなるだけピークに近い性能が出るようにしておくのが大事で、その上で全体でひとつの線形方程式を解く過程でのロードバランス、通信オーバーヘッド、 DGEMM 以外の処理のために9掛けとか8掛け（当然もっと悪いこともある）に差し引かれた実行性能が得られます。富士通の xGEMM は96%の効率を達成とのことで、HPC用プロセッサの面目躍如といったところでしょう。相場感としてはキャシュベースのプロセッサではせいぜい80%台、96%というのはスクラッチパッドの領域なのですが、セクタキャッシュという機能を利用してキャッシュミスを防いでいます。これは「たまたまそういう機能があったから使ってみたら速くなった」というのではなく、 xGEMM で最大限の性能が出せるようにという設計だったんじゃないかと推測しています（あくまでも個人的に）。
ここまで努力しても、「実アプリ的ではない」と一蹴されてしまうHPL、なんだか気の毒ですね。実アプリとかけ離れているとしたら、極端に高い効率でしょう。HPLで効率50%を割ったら「何かおかしいんじゃない？」という具合になりますが、実アプリで50%を超えるのというのは珍しいものです。 xGEMM でここまで高い効率が出せるのは、ブロック化によってmemory-wallを回避できているからです。ブロックサイズ $b$ に対して、行列行列乗算なら $O(b^3)$ の演算になるのに対して、メモリアクセスは $O(b^2)$ です。演算あたりのメモリアクセスが $O(1/b)$ になるので、（キャッシュを上手に使えていれば）一定以上の $b$ では主記憶アクセスネックにならないわけですね。アセンブラでべったりとレジスタを割り付けるように書かれていて命令レイテンシが隠蔽できるというのも大きいでしょう。
じゃぁ $b$ をどんどん大きくすれば帯域をケチりまくったHPL専用プロセッサを作れるかというとそこまで話は簡単でもないんですよね。 $b$ を2倍にすることで主記憶のB/F要求は半分にできますが、ロードバランスを維持するためには $N$ も2倍にすることになり、ノードあたりの搭載メモリが4倍になります。これだけなら帯域と容量のトレードオフなのですが、恐ろしいのはベンチマーク時間が8倍になってしまうことです（インタコネクト帯域も半減できるというメリットはあります）。あとノードあたりの行列サイズを固定してノード数を増やしていった場合、ノード数が4倍になるとベンチマーク時間が2倍になっていくというルールも、計測への負担となります。計算上、ノード数を64倍にしたら主記憶容量を1/4にし、主記憶とインタコネクト帯域を2倍にすることで実行時間を固定できるので、大規模な並列計算機になるほど広帯域で小容量のメモリを搭載するというのはHPLの実行時間にとっても理にかなった話となっています。「京」から「富岳」では総主記憶容量は4倍弱なので演算数が8倍弱、性能は40倍強となっており、計測は1/5程度の時間になり（一発で通ったのなら）楽になっただろうと想像します。

「京」のときの話になりますが、このような資料があったので引用させてください。

「一発勝負ではありません」には禿同（古い）です。
#HPCG

HPCGに関しては勉強会の資料がないのので代わりにこんなのはいかがでしょう：

「アプリケーションを表すモデルが線形方程式から微分方程式に移行し」
くわしい人は知っている．「Top500, Green500 の順位はもうスパコン性能の参考にならない」と順位リスト作成者が言い続けている

なかなかポエムポエム言い続けても天然物には勝てませんね。

ここでいう「微分方程式」はおそらく「偏微分方程式」のことです。偏微分方程式一般を直接解ける計算機はありませんが離散化することで線形方程式のかたちに落とし、その線形方程式を解いています。
解くべき方程式は

A \boldsymbol{x} = \boldsymbol{b}

あれっ、HPLと同じ？

　シングルヘル……シングルヘル……

違うのは行列 $A$ の性質とその解法です。
LINPACKで解いているのは「密行列」といって行の中の全ての要素に値が入っています。
いっぽうHPCGで解くのは「疎行列」といって、行の中で値が入っているのは対角成分ひとつとあとはいくつかの非対角成分のみ、残りの要素は0です。HPCGでは非対角要素は26個、一様3次元メッシュ¹の上下左右前後と斜めの成分です。
これだけ聞くと密行列の方が偉そう／難しそう感がありますが、扱える次元数が違います。密行列は格納するのに $N^2$ のメモリが必要ですが、疎行列なら値が0のところは詰めて格納することで $N\times(非対角要素数+1)$ で済みます。なので疎行列を密行列として扱って解くというのは $N$ がよほどか小さくない限りは行われません。

\boldsymbol{r}_i := \boldsymbol{b} - A \boldsymbol{x}_i

のようなベクトル行列積を何度も行いながら解を改善させていきます。

　シングルヘル……

---

「なるほど、この疎行列ってのが実用的な行列で、密行列はベンチマーク専用行列ってことですね」
「あ〜の〜な〜（怒）」
「でも『密』は回避した方がいいんでしょ？」
「ギャフン！」

• 「京」の時代の資料になりますが、SS研での理研AICS南さんの資料（2014)
  にカラーリングによるチューニングを含むHPCGの詳細が書かれています。

• 昨日の青子守歌さんの記事は実際にこのベンチマークに直接携わった方による資料なので貴重です。

#Graph500
架空の対話：
「何でHPCの人達ってFP性能ばっか測ってるの？」
「じゃあ浮動小数点演算は一切しないベンチマーク作ってみよっか」

理研R-CCS中尾さんのスライドになります。
2010年からもう10年来のベンチマークになるわけですね。
ビッグデータ()とはいうものの、このベンチマークではスパコンのメモリ一杯に置いたグラフを辿り初めてから辿り終えるまでの時間を計測し、最短乗車距離とか最長乗車距離探索のような「アルゴリズム実行」をしているわけではない（いや辿るだけでもアルゴリズムですが）みたいです。ともかく一切FP演算をしないというのは潔さ、清々しさを感じます。
（5年ほど前の）チューニングで一気にスコアを数倍にし首位を奪還というのは劇的でリストの活性化にもつつながったかと思うのですが、スパコンの基礎体力テストをしているのか、アルゴリズムコンテストをしているのかどっちなんだろうという懸念はあるでしょう。（この資料の7枚目）

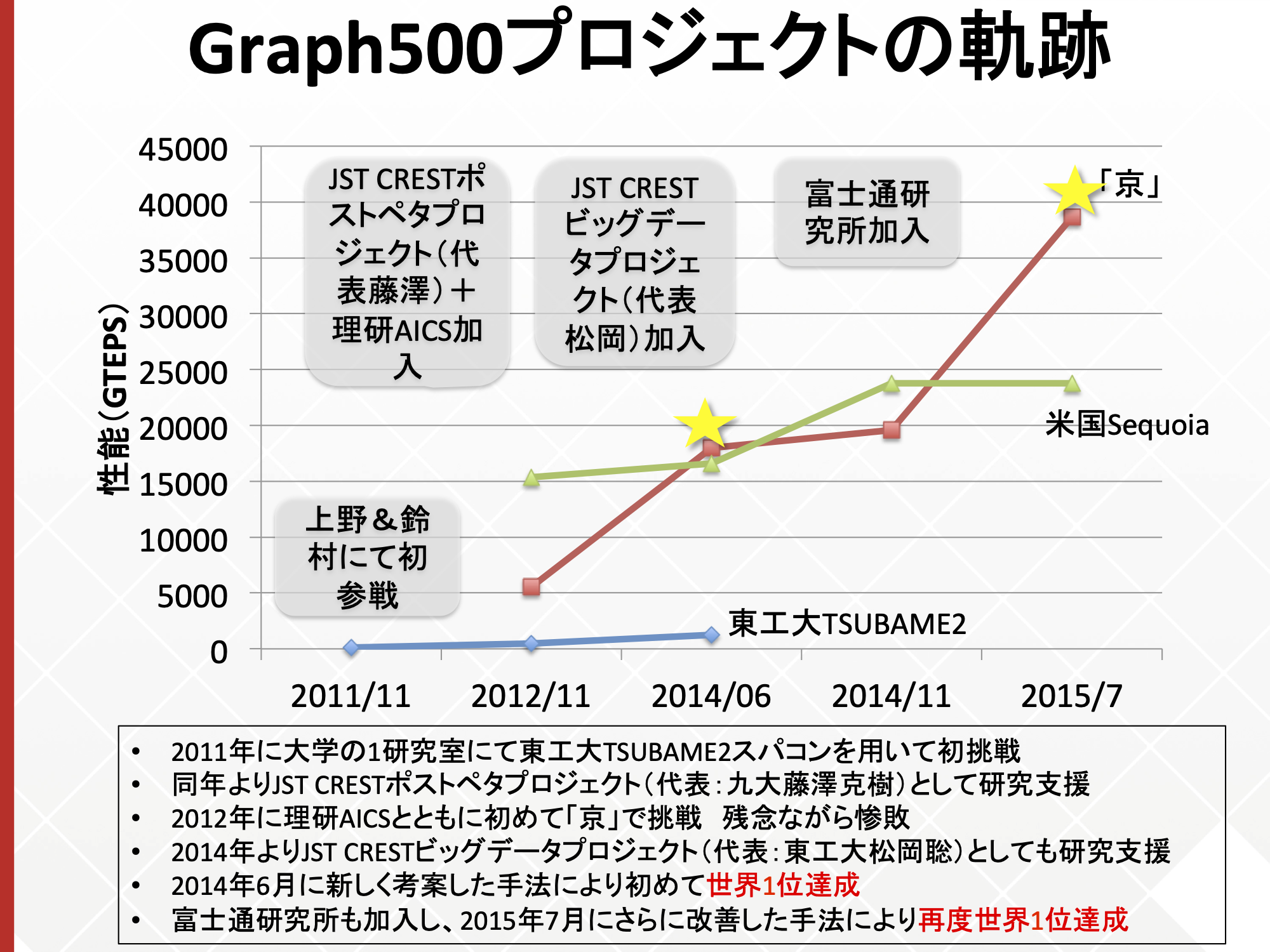
最近のGraph500のリストを見る限り、スコアはインタコネクトの総帯域を反映しているように見えます。「京」ではリンクあたり6.25 Gbps、x8レーンで（8b10b変換と仮定）5 GB/s、10リンクのうち最大4リンク同時通信で20 GB/sがピークのインジェクションでしたが、「富岳」では28 Gbps、x2レーン、6.8 GB/s、6 of 10リンク同時通信で40 GB/sのインジェクションとなります。SerDesの周波数が延びたのに対しておとなしい性能向上です。「富岳」では10あるリンクの1/4が光接続（QSFP28）になったのでその分のコストアップは勘定しなくてはと思いますが、「京」のときよりインタコネクトの原価率は下がってませんかね？
スコアは「京」の82,944ノードで32 TTEPS（テラテップス）、「富岳」の92,160ノードで71 TTEPS、「富岳」の158,976ノードで103 TTepsです。おおむね総インジェクションバンド幅を反映しているようにみえます。ただし中尾さんの資料を見る限りノード数が増えるにつれalltoallvの占める時間が増えており、トーラストポロジの弱点（インジェクションに対してバイセクションが弱い）が見えてきているのかもしれません。

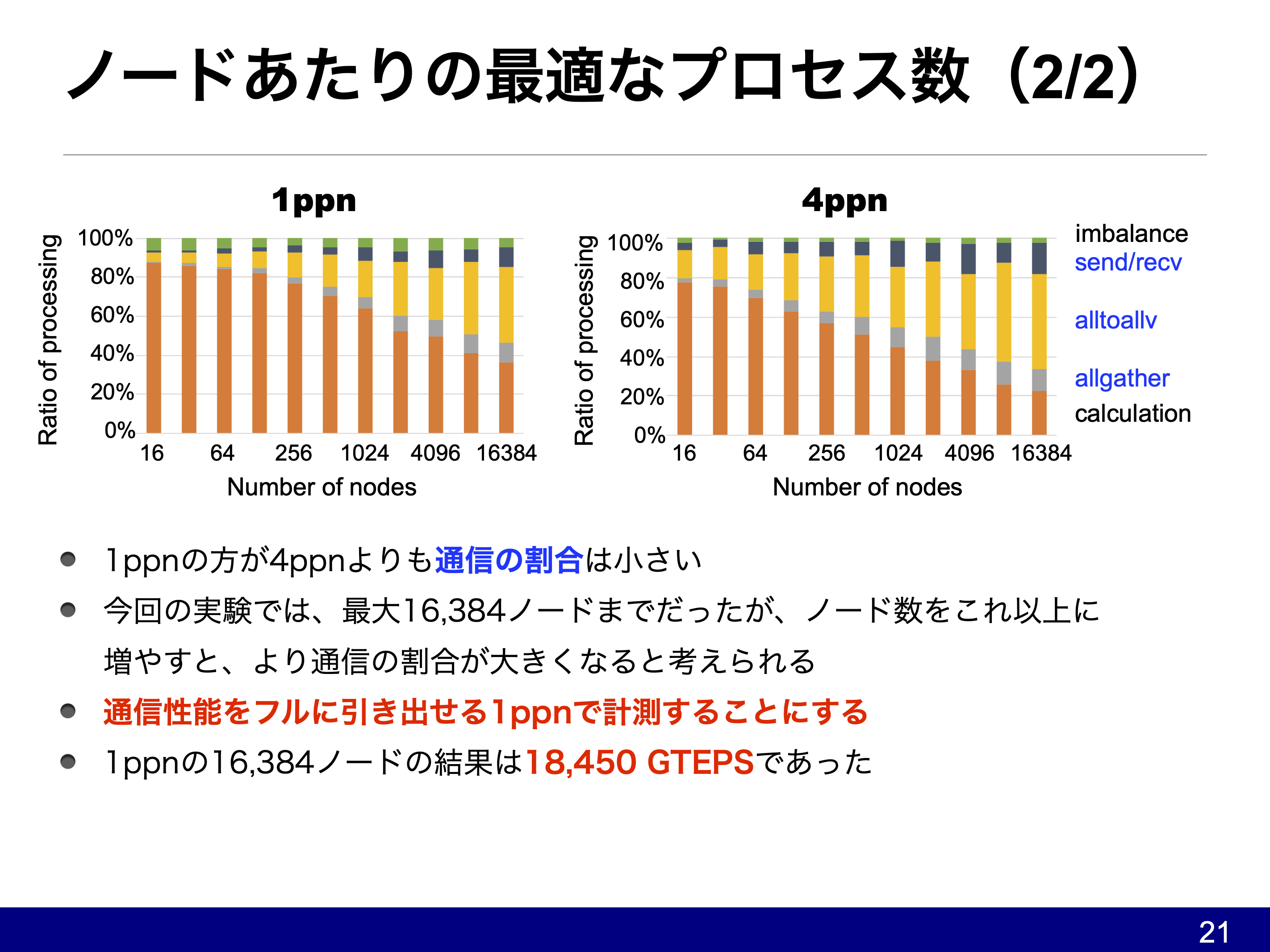
（ppnというのはprocess per nodeで、ノードあたり48スレッドの1プロセスが1ppn、12スレッドの4プロセスが4ppnとなります。富岳では1,2,4,8,12,16,24,48ppnどれでも動くはず。）

ついでの話なのですが、3次元の隣接通信を行うHPCGを以外のHPL、Graph500、HPL-AIでは縦横の2次元にコミュニケータ分割を行っていました。

24 \times 23 \times 24 \times 2 \times 3 \times 2 = (24 \times 23) \times (24 \times 2 \times 3 \times 2) = 552 \times 288 = 158,{}
976

みたいなマッピングを3つのグループで独立に行っていたみたいです。

まだよくわかっていないのは、TEPSがネットワーク帯域（特にインジェクション）をどのぐらい消費（消化）しているのかという換算レートです。200 Gbpsのリンクが10万ポートあるシステムなら確実に首位奪取できそうなのですが、近い将来にそういうシステムが現れるかどうか……

　シングルヘル……

特定のマシンがずっとトップに居座ると、誰も対抗しようとしなくなってリストごと死んでしまわないかというのが少し心配……

#HPL-AI
架空の対話：
「結局実アプリは疎行列なんでしょ？」
「いやいや、最近じゃAIは密行列なんじゃよ」
「でも倍精度いらないでしょ？」
「一理あるのぅ」

別名「混合精度LINPACK」といって、LINPACK同様の密行列を解くのに単精度や半精度の利用を認めたベンチマークです。AIでいう学習や推論を行っているわけではありません。
リストはこちら。2019/11のときは我々はルールも知らなかったと思うのですが……2020/06と2020/11では富岳が1.42 EFLOPS、2.00 EFLOPSで連覇となっています。
理研R-CCSの工藤さんの発表資料はこちらになります。
単に低い精度で解くだけでは、解の精度も低下してしまいます。HPL-AIでは

• LU分解そのものは低精度で行って良い
• 低精度で求めた$U^{-1}L^{-1}$を逆行列の近似として反復解法を適用する

ことで最終的に倍精度の解を求めるようになっています。また、問題となる行列 $A$ についてもHPLから変更されており

• 対角優位にすることで低精度でもLU分解が破綻しない
• HPLでは必須だったpartial pivotingが不要になった

というものがあります。Pivotingが不要というのはベンチマークプログラムを実装する側としては並列度も増えるし実装項目もバグもテストも減るので良いことずくめなのですが、工藤さんにとっては「簡単すぎた⁴」いう不満が残ったのかもしれません。

　シングルヘル……

ここで少しHPCにおける混合精度の思い出などを。SSE/SSE2ぐらいの時代から数値計算を始めたような世代では、SIMDなら単精度が倍精度より倍のスループットがあるとういうのが自然な感覚だったりします。でもHPC用のプロセッサを見てみるとそうでもなく、単精度は倍精度と同じFLOPSという石も少なくありません。京、BlueGene/{L,P,Q}、TaihuLighit、Aurora Tsubasa以前のSXなどが該当します。GPUの影響なのかSSEなのかはたまたAIなのか、最近のHPCアプリ／ベンチマークでは単精度やより低精度の演算性能にも注目するようになってきています。以前でもトランジスタが余っていたのかどうかはともかくとして、最近の方がより低精度演算にもトランジスタを使う方向になってきているみたいですね。

---

シングルヘル……

俺たちの2020年はこれからだ！

1. なので本当は構造格子の問題をあえて非構造格子として解くというベンチマークになっています。実は構造格子であることを利用して高速化することはベンチマークのルールで禁止されています。
   HPLでやっていたのは「密行列を直接法（LU分解法）で解く」というものだったのに対してHPCGは「疎行列を反復法（CG法²）で解く³」というベンチマークになっています。直接法では行列そのものを変形していくわけですが、反復法では ↩

2. 本当のことをいうと、 CG法は高々 $N$ 回の反復で収束する（ただし丸め誤差がない場合）ため直接法と反復法の両方の性質を併せ持つのですが、実質的に反復法と数えられることが多いです。 ↩

3. ベンチマーク時間の都合なのか、最後まで解いてはいないようです。
   本当は前処理（マルチグリッドとガウス＝ザイデル法）もあるのでもっと複雑なのですが、この疎行列ベクトル積の計算はメモリアクセスの非常に多い、現代の計算機ではほぼメモリネックになってしまう処理となっています。行列はシーケンシャルアクセスにはできるものの再利用性がなく（1語読んで1回積和したらポイ）、ベクトルはある程度キャッシュが効くもののギャザーアクセスになります。前処理に現れるマルチカラー化したガウス＝ザイデル法の部分も大体同じです。
   結局、リストに載るようなちゃんとチューニングされたコードではほぼ主記憶帯域幅を反映した性能になっているようです。いちおうFLOPS値やHPLとの性能比がリストに表示されるわけですが、「実効帯域／ピーク帯域」みたいな表示になっていてくれた方がわかりやすいかなとも思います（B/F=6を仮定してFLOPS値に掛けたのが実効帯域の目安）。逆に（HPLのときでもそうですが）主記憶帯域から期待できるスコアからあまりにも低い効率しか出ていない場合、コードか計算機の何処かがおかしいのでは、ということになります。
   なんだかんだいって、主記憶帯域で律速される非構造格子・疎行列解法のアプリ（実アプリの全てではないものの重要な位置を占める）の性能予測となるベンチマークとしてHPCGは定着してきたように思います。新しい計算機が入ったときに計測してサブミットしてもらえるようになって初めて、リストは生き永らえますから…… ↩

4. 経歴をみるとKNCでのチューニング経験があるようです。石としては失敗とされても人材育成には成功してるんじゃ……
   「簡単になった」ということで、「富岳」全系で計測できた2020/11の結果ではHPLの4.5倍の性能値となっています。ピーク性能比では倍：単：半が1:2:4なので、4倍を超えたspeed upはpivotが無い分とかその他チューニングの効果といってよいでしょう。対してGPU勢なのですが、Seleneが丁度4倍ですが他のシステムは4倍に届いていません。TensorCoreのピークは倍精度の16倍あったはずで、チューニングの程度がHPLには追いついていないのかもしれません。SummitのTensorCoreピークは3.3 EFLOPSあるので、6割ちょっとの効率が出るまでチューニングできれば富岳を超えてくるんですね。なのでこのベンチマークのリストが死んでしまわなければ、HPL-AIは富岳が最初に失冠するベンチマークの可能性が高いでしょう。ただまだリストもできたばかりで登録サイト数も限られています。チューニングによる逆転劇などが起きてリストが活性化してくれれば、と願っています。 ↩