対数正規分布の確認

#1.概要
対数正規分布について、どんな分布かイメージできていなかったのでサンプルデータを作って確認した。

2.対数正規分布のヒストグラム確認

確率変数$X$を自然対数で変換した$\log{X}$が$N(\mu,\sigma)$に従うとき、$X$は対数正規分布に従うという。
($X \sim LN(\mu,\sigma)$と表現)

この分布の乱数を生成するのがnp.random.lognormal。
これが上の定義に従っているか確認(疑っているのではなく勉強のための確認)。

##2.1.サンプルデータの準備

以下で乱数を生成。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import norm

np.random.seed(1) #乱数を再現できるようにnp.random.seed(1)としておく
df_smpl=pd.DataFrame() #DataFrameに複数サンプルデータを格納する
df_smpl['$\mu$2_$\sigma$1'] = np.random.lognormal(2, 1, 5000) # mu=2, sigma =1
df_smpl

	𝜇 2_ 𝜎 1
0	37.500166
1	4.007805
2	4.357194
3	2.526996
4	17.556208
...	...
4995	36.764997
4996	13.021646
4997	3.400805
4998	21.865033
4999	69.546074

##2.2.ヒストグラム確認

まず生成した乱数をそのままの状態で(自然対数での変換なしで)分布を確認。以下のコードを使用。

plt.hist(df_smpl['$\mu$2_$\sigma$1'], 500, density=True, align='mid',
         label='hist:$ \mu=2,\sigma=1$',
         alpha =0.5)
plt.xlim([0,50])
plt.legend()
plt.show()

次に自然対数での変換して、その分布を確認する。最初に以下で変換。

df_smpl_log = np.log(df_smpl)

	𝜇 2_ 𝜎 1
0	3.624345
1	1.388244
2	1.471828
3	0.927031
4	2.865408
...	...
4995	3.604546
4996	2.566613
4997	1.224012
4998	3.084889
4999	4.241989

次にヒストグラムを確認。

count, bins, ignored = \
  plt.hist(df_smpl_log['$\mu$2_$\sigma$1'], 50, density=True, align='mid',
          label='hist:$ \mu= 2,\sigma= 1$',
          alpha =0.5)
x = np.linspace(min(bins), max(bins), 10000)

pdf_N = (np.exp(-(x - 2)**2 / (2 * 1**2)) / (np.sqrt(2 * np.pi) * 1 ))
plt.plot(x, pdf_N,color='black',linestyle="dashed",
        label='pdf:$ \mu= 2,\sigma= 1$')

plt.legend()
plt.show()

ダッシュ線は正規分布$N(2,1)$の確率密度分布関数。
⇒np.random.lognormalを乱数を自然対数で変換したものの分布は正規分布に従うことを確認した。
⇒ np.random.lognormal`で生成したデータは対数正規分布に従うことを確認した。

3.対数正規分布のパラメータ依存確認

np.random.lognormalで乱数を生成するときには$\mu$と$\sigma$の2つのパラメータを設定した。
これらのパラメータをかえることで分布がどう変わるか確認する。

3.1.サンプルデータの準備

以下で$\mu$と$\sigma$の組み合わせ6通りのデータを生成。

np.random.seed(1)

mus = [2,3,4,2,2]
sigmas= [1,1,1,0.5,0.3]

for mu,sigma in  zip(mus, sigmas):
    df_smpl['$\mu$'+str(mu)+'_'+'$\sigma$'+str(sigma)] = np.random.lognormal(mu, sigma, 5000)
df_smpl

	𝜇 2_ 𝜎 1	𝜇 3_ 𝜎 1	𝜇 4_ 𝜎 1	𝜇 2_ 𝜎 0.5	𝜇 2_ 𝜎 0.3
0	37.500166	7.966496	48.304566	11.305818	4.139317
1	4.007805	62.108937	68.591582	4.276042	7.041859
2	4.357194	6.496144	38.386079	11.343875	5.756526
3	2.526996	9.730472	23.794312	15.435313	6.946004
4	17.556208	37.471146	42.052136	4.359153	10.053054
...	...	...	...	...	...
4995	36.764997	21.605730	35.628226	4.610774	9.728639
4996	13.021646	32.756524	423.913299	10.925591	4.245695
4997	3.400805	7.285282	27.500616	24.636200	10.007116
4998	21.865033	18.864914	132.981963	11.489031	7.465049
4999	69.546074	4.768969	43.057696	7.030106	7.010456

以下の組み合わせでパラメータ$\mu,\sigma$の依存性を確認。
$\mu$依存確認：$(\mu,\sigma) = (2,1),(3,1),(4,1)$
$\sigma$依存確認：$(\mu,\sigma) = (2,1),(2,0.5),(2,0.3)$

3.2.μ依存確認

対数正規分布の$\mu$の変化に対する分布の変化を確認。

display(df_smpl[['$\mu$2_$\sigma$1','$\mu$3_$\sigma$1','$\mu$4_$\sigma$1']])

for mu,sigma in zip([2,3,4],[1,1,1]):
    count, bins, ignored = \
      plt.hist(df_smpl['$\mu$'+str(mu)+'_'+'$\sigma$'+str(sigma)], 500, 
               density=True, align='mid',
               label='hist:$ \mu= $'+ str(mu)+'$,\sigma= $'+ str(sigma),
               alpha =0.5)
plt.xlim([0,50])
plt.legend()
plt.show()

	𝜇 2_ 𝜎 1	𝜇 3_ 𝜎 1	𝜇 4_ 𝜎 1
0	37.500166	7.966496	48.304566
1	4.007805	62.108937	68.591582
2	4.357194	6.496144	38.386079
...	...	...	...
4999	69.546074	4.768969	43.057696

$\mu$の増加に伴い、ピーク値が大きくなり裾が広がる(最頻値が大きくなり、分散が大きくなる)ことを確認した。

##3.3.σ依存確認

対数正規分布の$\sigma$の変化に対する分布の変化を確認。

display(df_smpl[['$\mu$2_$\sigma$1','$\mu$2_$\sigma$0.5','$\mu$2_$\sigma$0.3']])

for mu,sigma in  zip([2,2,2],[1,0.5,0.3]):
    count, bins, ignored = \
      plt.hist(df_smpl['$\mu$'+str(mu)+'_'+'$\sigma$'+str(sigma)], 500,
               density=True, align='mid',
               label='hist:$ \mu= $'+ str(mu)+'$,\sigma= $'+ str(sigma),
               alpha =0.5)
plt.xlim([0,20])
plt.legend()
plt.show()

	𝜇 2_ 𝜎 1	𝜇 2_ 𝜎 0.5	𝜇 2_ 𝜎 0.3
0	37.500166	11.305818	4.139317
1	4.007805	4.276042	7.041859
2	4.357194	11.343875	5.756526
...	...	...	...
4999	69.546074	7.030106	7.010456

$\sigma$の減少に伴い、ピーク値が大きくなり裾が狭まる(最頻値が大きくなり、分散が小さくなる)ことを確認した。
($\sigma$の増加に伴い、ピーク値が小さくなり裾が広がる(最頻値が小さくなり、分散が大きくなる)ことを確認した。)

4.対数正規分布の確率密度関数との対応確認

ここまで確認した内容と、確率密度関数・最頻値・分散との対応を確認する。

確率密度関数$f_{NL}(x)$、最頻値$x_{mode}$と分散$V[X]$は以下のように求まる。
(式の導出などはごちゃごちゃするので最後に書く)

$f_{NL}(x) = \frac{1}{\left( \sqrt{2 \pi} \right)\sigma x }\exp \left[ - \frac{(\log{x} -\mu )^2 }{2 \sigma ^2} \right] $

$x_{mode} = \exp[\mu - \sigma^2] $

$V[X] ＝\exp{ \left[ 2\mu + \sigma^2 \right] } \left( \exp{ [ \sigma^2 ] }-1 \right) $

##4.1 分布の確認

$f_{NL}(x)$と確認したデータ分布を重ねてグラフを作成。
$f_{NL}(x)$は以下でpdf_NLとしてコードに記入。グラフは黒のダッシュ線で表示。

$f_{NL}(x) = \frac{1}{\left( \sqrt{2 \pi} \right)\sigma x }\exp \left[ - \frac{(\log{x} -\mu )^2 }{2 \sigma ^2} \right] $
pdf_NL = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))/ (np.sqrt(2 * np.pi) * sigma * x ))

確率密度関数と乱数から生成したデータの分布との対応関係を確認する。
以下、確率密度関数を重ねたグラフを出力するコード。

for mu,sigma in zip([2,3,4],[1,1,1]):
    count, bins, ignored = \
      plt.hist(df_smpl['$\mu$'+str(mu)+'_'+'$\sigma$'+str(sigma)], 500, 
               density=True, align='mid',
               label='hist:$ \mu= $'+ str(mu)+'$,\sigma= $'+ str(sigma),
               alpha =0.5)
                                    
    x = np.linspace(min(bins), max(bins), 10000)
    pdf_NL = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
              / (np.sqrt(2 * np.pi) * sigma * x ))
    plt.plot(x, pdf_NL,color='black',linestyle="dashed",
             label='pdf:$\mu= $'+ str(mu)+'$, \sigma= $'+ str(sigma))

plt.xlim([0,50])
plt.legend()
plt.show()

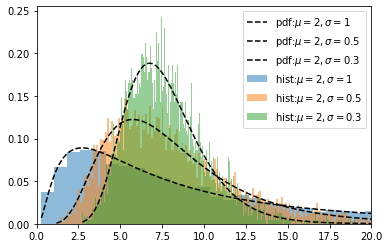
for mu,sigma in  zip([2,2,2],[1,0.5,0.3]):
    count, bins, ignored = \
      plt.hist(df_smpl['$\mu$'+str(mu)+'_'+'$\sigma$'+str(sigma)], 500,
               density=True, align='mid',
               label='hist:$ \mu= $'+ str(mu)+'$,\sigma= $'+ str(sigma),
               alpha =0.5)
                                    
    x = np.linspace(min(bins), max(bins), 10000)
    pdf_NL = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
              / (np.sqrt(2 * np.pi) * sigma * x ))
    plt.plot(x, pdf_NL,color='black',linestyle="dashed",
             label='pdf:$\mu= $'+ str(mu)+'$, \sigma= $'+ str(sigma))
    
plt.xlim([0,20])
plt.legend()
plt.show()

確率密度分布関数$f_{NL}(x)$がnp.random.lognormalで生成したデータの分布にフィットすることを確認した

##4.2 最頻値と分散の確認

この最頻値$x_{mode}$と分散$V[X]$の式は以下の通り(再掲。導出は最後)

$x_{mode} = \exp[\mu - \sigma^2]$
$V[X] ＝\exp{ \left[ 2\mu + \sigma^2 \right] } \left( \exp{ [ \sigma^2 ] }-1 \right) $

この式とデータの分布から確認した以下の結果は整合することを確認した。
$\mu$の増加に伴いピーク値(最頻値)が大きくなる。
$\sigma$の増加に伴いピーク値が小さくなる。

4.3.式の導出

###【確率密度関数の導出】
以下をもとに確率密度関数を導く。(青色は式変形した箇所)

確率変数$X$を自然対数で変換した$\log{X}$が$N(\mu,\sigma)$に従うとき、$X$は対数正規分布に従うという。
($X \sim LN(\mu,\sigma)$と表現)

$y=\log{x}$は正規分布に従うので以下の(1)が成り立つ。

\begin{eqnarray}
f_{N}(y) = \frac{1}{\left( \sqrt{2 \pi} \right) \sigma}\exp \left[ - \frac{(y -\mu )^2 }{2 \sigma ^2} \right] \tag{1}
\end{eqnarray}

対数正規分布の確率密度関数を$f_{NL}(x)$とすると、以下の(2)の関係が成り立つ。

\begin{eqnarray}
f_{NL}(x)=f_{N}(y)  \left| \frac{\partial y}{\partial x} \right|  \tag{2} 
\end{eqnarray}

(1),(2)より対数正規分布の確率密度関数(3)が得られる。

\begin{eqnarray}
f_{NL}(x) &=& \frac{1}{\left( \sqrt{2 \pi} \right)\sigma  }\exp \left[ - \frac{(\log{x} -\mu )^2 }{2 \sigma ^2} \right] \left| \frac{\partial y}{\partial x} \right| \\
  &=& \frac{1}{\left( \sqrt{2 \pi} \right)\sigma \color{blue}{x} }\exp \left[ - \frac{(\log{x} -\mu )^2 }{2 \sigma ^2} \right] \tag{3}
\end{eqnarray}

###【最頻値の導出】

最頻値$x_{mode}$は$f'_{LN}(x)=0$を満たす$x$である。

\begin{eqnarray}
f'_{LN}(x) = -\frac{1}{\left( \sqrt{2 \pi} \right) \sigma x} \frac{1}{x^2} \exp{\left[ - \frac{( \log{x} - \mu)^2)}{2 \sigma^2} \right]}\left( 1+ \frac{\log{x} - \mu}{\sigma^2} \right) = 0 \tag{4}
\end{eqnarray}

(4)式より最頻値$x_{mode}$は以下である。

\begin{eqnarray}
x_{mode} = \exp[\mu - \sigma^2] \tag{5}
\end{eqnarray}

　
###【分散の導出】

\begin{eqnarray}
V[X] &=& E[X^2] - \left( E[X] \right) ^2 \\
&=& \exp{ \left[ 2\mu + 2\sigma^2 \right] } - \left( \exp{ \left[ \mu - \frac{\sigma^2}{2} \right] } \right) ^2 \\
&=& \exp{ \left[ 2\mu + \sigma^2 \right] } \left( \exp{ [ \sigma^2 ] }-1 \right)  \tag{6}
\end{eqnarray}

(6)式で用いられる$E[X],E[X^2]$の導出は以下の通り。

\begin{eqnarray}
E[X] &=& \int^{\infty}_{0} x f_{LN}(x) dx \\
  &=& \int^{\infty}_{0} x \color{blue} {\frac{1}{\left(  \sqrt{2\pi} \right) \sigma}\frac{1}{x}
       \exp \left[ - \frac{ (\log{x}-\mu )^2 }{2\sigma} \right]}dx \\
 &=&  \int^{ \color{blue}{\infty} }_{ \color{blue}{- \infty}} \color{blue}{e^{y}} \frac{1}{\left(  \sqrt{2\pi} \right)\sigma}\exp \left[ - \frac{ (y-\mu )^2 }{2\sigma} \right] \color{blue}{dy}\\

 &=&  \int^{\infty}_{- \infty} \frac{1}{\left(  \sqrt{2\pi} \right)\sigma}\exp \left[ \color{blue}{ y } - \frac{(y-\mu)^2}{2\sigma^2} \right] dy\\
 &=&  \color{blue}{ \exp{\left[ \mu + \frac{\sigma^2}{2}   \right]}} \int^{\infty}_{- \infty}  \frac{1}{\left(  \sqrt{2\pi} \right)\sigma} \color{blue}{ \exp \left[ - \frac{\{ y-(\mu + \sigma^2) \}^2}{2\sigma^2} \right] } dy\\
 &=&  \exp{\left[ \mu + \frac{\sigma^2}{2}   \right]} \tag{7}
\end{eqnarray}

\begin{eqnarray}
E[X^2] &=& \int^{\infty}_{0} x^2 f_{LN}(x) dx \\
  &=& \int^{\infty}_{0} x^2 \color{blue}{ \frac{1}{\left(  \sqrt{2\pi} \right) \sigma}\frac{1}{x}
       \exp \left[ - \frac{ (\log{x}-\mu )^2 }{2\sigma} \right] } dx \\
 &=&  \int^{ \color{blue}{\infty} }_{ \color{blue}{- \infty}} \color{blue}{e^{2y}} \frac{1}{\left(  \sqrt{2\pi} \right)\sigma}\exp \left[ - \frac{ (\color{blue}{y}-\mu )^2 }{2\sigma} \right] \color{blue}{dy}\\

 &=&  \int^{\infty}_{- \infty} \frac{1}{\left(  \sqrt{2\pi} \right)\sigma}\exp \left[ \color{blue}{ 2y } - \frac{(y-\mu)^2}{2\sigma^2} \right] dy\\
 &=&  \exp{ [ 2\mu + 2\sigma^2  ]}  \int^{\infty}_{- \infty}  \frac{1}{\left(  \sqrt{2\pi} \right)\sigma}\color{blue}{ \exp \left[ - \frac{\{y-(\mu + 2\sigma^2) \}^2}{2\sigma^2} \right] }  dy\\
 &=&  \exp{\left[ 2\mu + 2\sigma ^2  \right]} \tag{8}
\end{eqnarray}

以上