はじめに
https://atcoder.jp/contests/abc128/tasks/abc128_e
こちらの問題ために、どうしても
「要素の追加・削除・最小値探索を高速に出来る方法」
が欲しくなったのですが、Rubyのデフォルトにはなさそうだったので、今後の為に自分で作りました。
ヒープ・優先度付きキュー(priority_queue)みたいなやつです。
ヒープとは[1]
ヒープは半順序集合をツリーで表現したデータ構造です。親ノードは、子ノードよりも小さい(あるいは大きい)か等しいという条件を満たすツリー構造になります。
とあります。
今回は 親ノードは、子ノードよりも小さい の方(最小ヒープ)の話をしてきます。
実際のヒープ
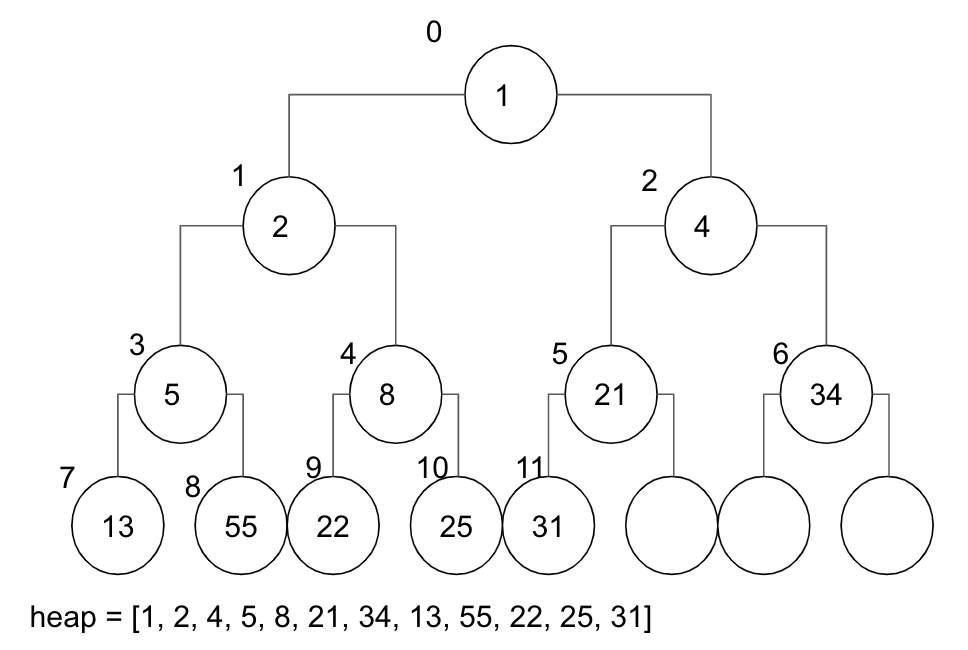
実際にはこんな感じの木構造です。
親のほうが小さい、というだけのルールに則って数字を並べているだけです。
親のほうが小さいというルールに従っている状態で、ノードの追加・削除を行っていると、最小値は常に0番目のノードになります。
ツリー構造の各ノードやその親子関係を、Arrayで表現します。
あるノードのindexをi(i = 0,...)としたとき、
その子のindexは (i << 1) + 1 と (i << 1) + 2
その親のindexは (i - 1) >> 1 で計算できます。( >> << はビットシフトです)
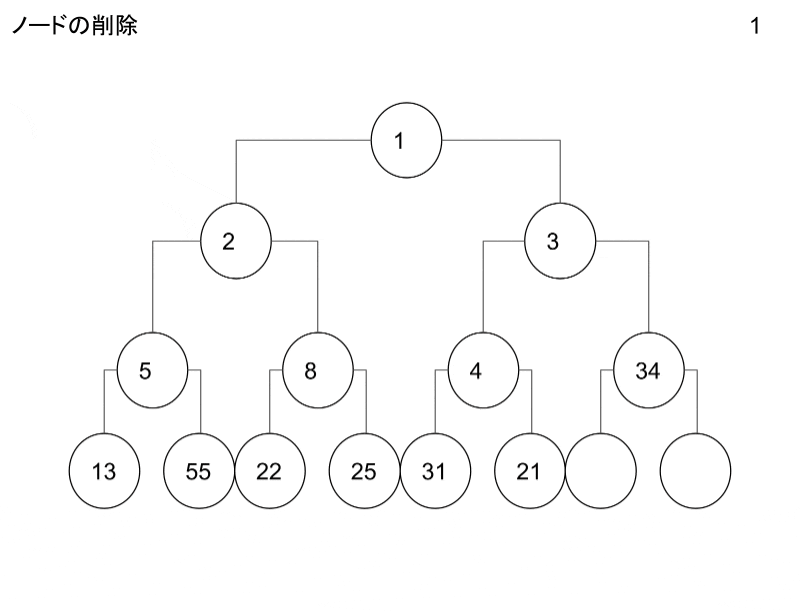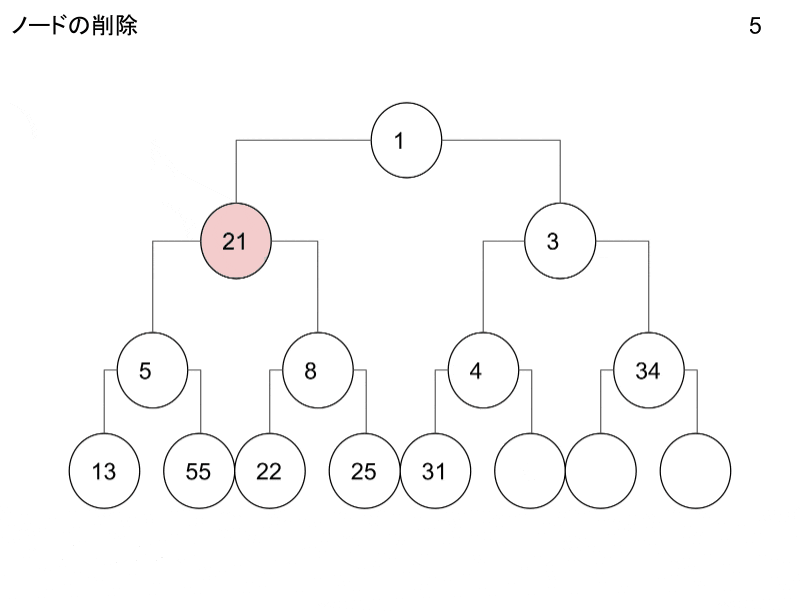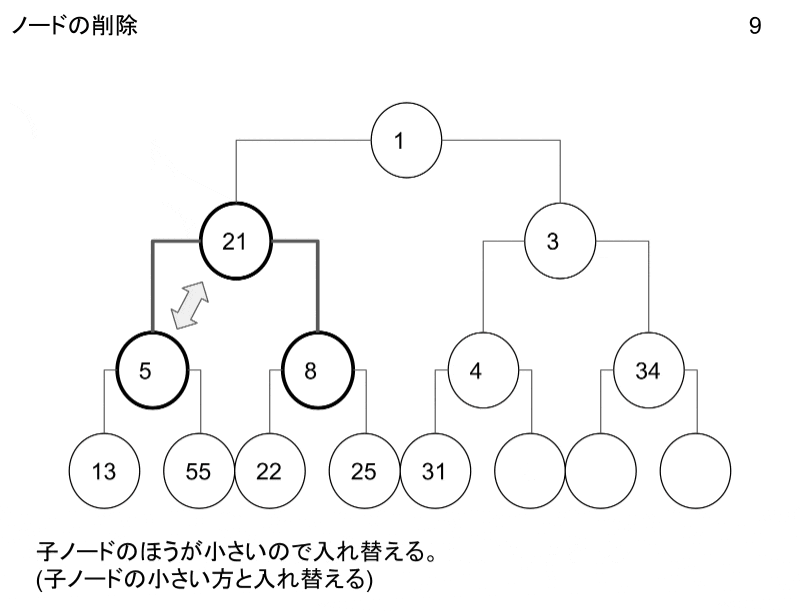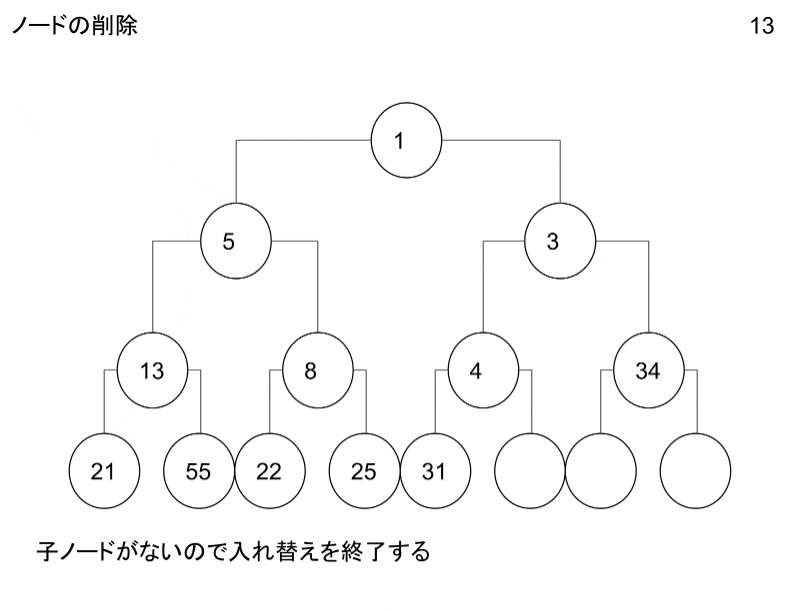
ノードの追加・削除
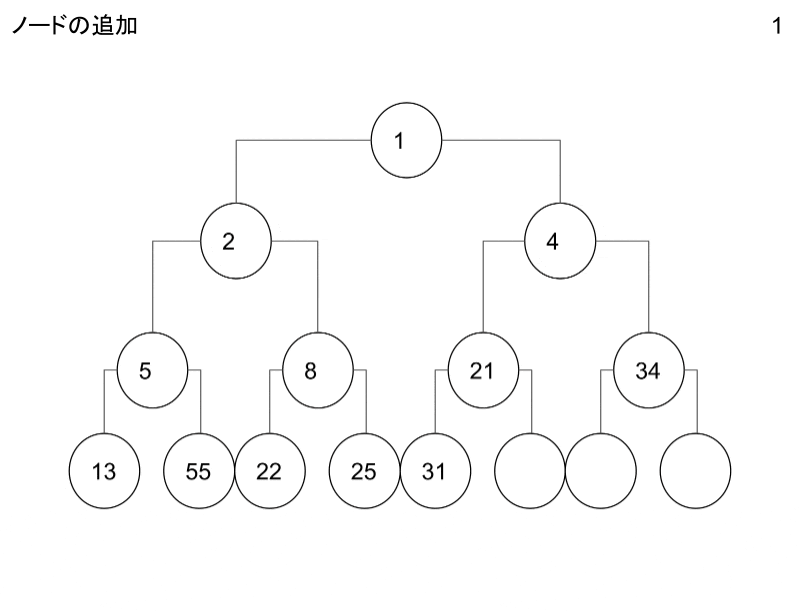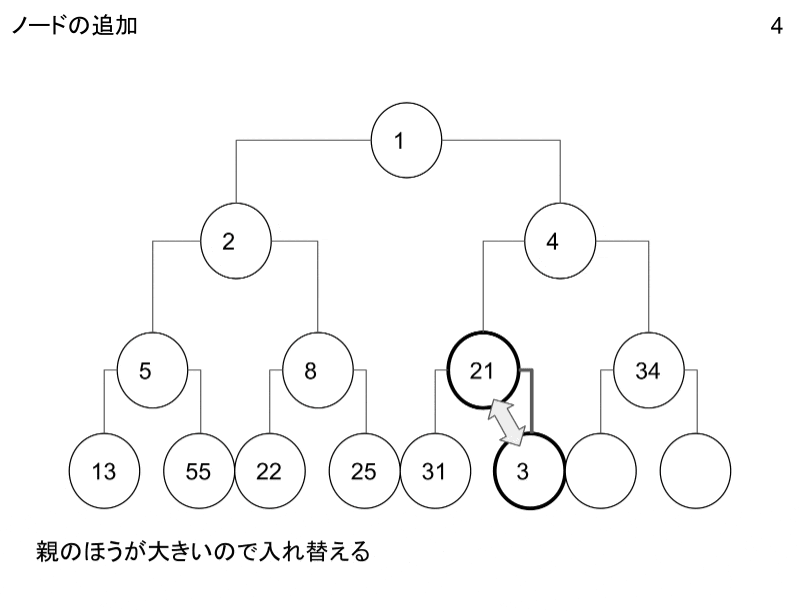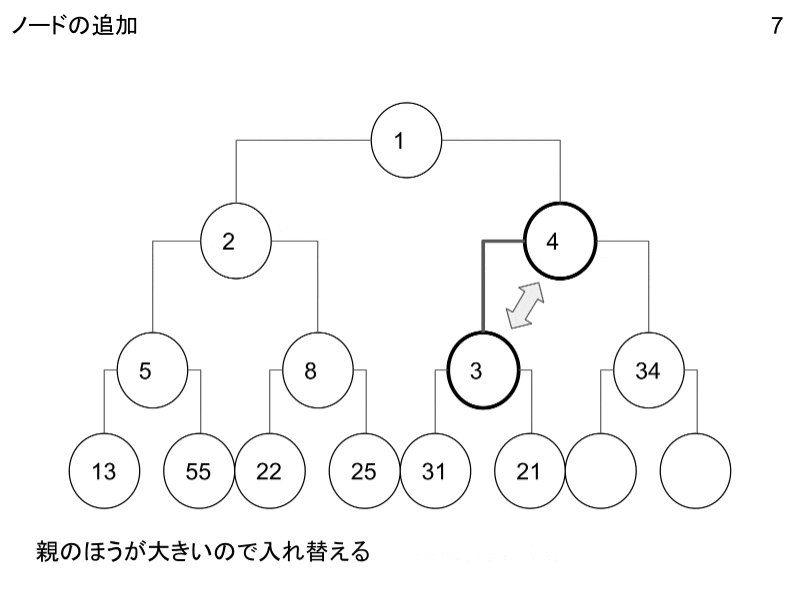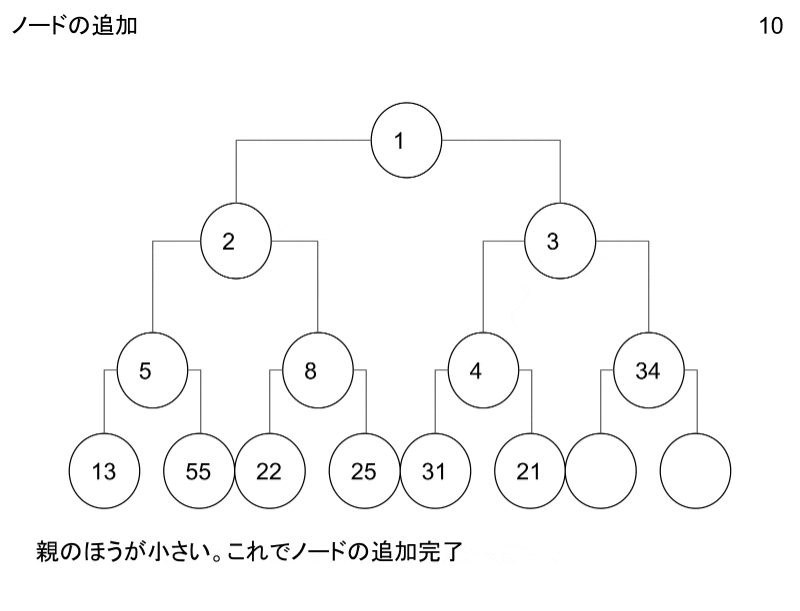
ノードの追加・削除の操作についてです。
GIFにしたのでこちらを御覧ください。
結局何が良いの?
最小値を知りたいだけの場合には効率が良いです。
値の挿入・削除はノード数Nに対してO(logN)で行えます。最小値の探索はO(1)です。
要素が2^10=1024個ぐらいあっても、木の高さは10程度なので、
追加・削除があっても入れ替えは10回(log(2^10)=10)ぐらいしか起こりません。
普通のArrayの場合は
要素を追加はO(1)ですが、削除はO(N)かかります。
最小値探索したい場合は、O(N)かかります。
(削除したら、それよりも後ろの要素を全部前に一つずつずらすのでO(N)です)
要素の追加しか行われず、
最後に1回だけ最小値を聞かれるならArrayほうが高速です。
まあそんな場合はArrayに数字を入れたりせず、
常に最小値だけを持って入力を待つだけで良いのですが。
bsearchとinsertを組み合わせArrayを常にソート済みで使う場合、
要素の追加は、挿入場所を探すのにO(logN)、挿入にO(N)。
削除はO(N)、最小値探索はO(1)です。
(最小値ではなく、何度もx番目に小さい値を聞かれるような場合には、こちらのほうが高速かもしれません)
ランダウの記号知らない人いないと思いますが一応載せておきます。
https://ja.wikipedia.org/wiki/ランダウの記号
O(logN)なら、要素がNからN^10に変わっても、10倍の時間ぐらいで済む操作ということです。
実装
実際の実装です
https://github.com/k-karen/ruby-samples/blob/master/heap/myheap.rb
値を引数に要素の追加・削除を行う都合上、
重複要素の追加は出来ません。(ゆるして)
各メソッドについて軽い説明をしていきます。
上のgithubのURLからご確認いただけるmyheap.rbです(長いので閉じておきます)
class Heap
def initialize(n)
@nodes = Array.new(n)
@index = Hash.new
@size = 0
end
def push(current_value)
# 存在する値ならpushしないでreturn (入力を信じるのであれば、必要無い確認)
return if @index[current_value]
# 今から値を入れるのは、@size番目
# 0番目...@size-1までの@size個の要素が元々あるから。
current_index = @size
@size += 1
# 末端に要素を追加した時、その値が小さければ、どんどん親ノードへ上がっていく。
while current_index > 0 do
# 親ノードのindexは (i-1) >> 1 で計算できる
# 親より自分が大きいなら、入れ替え不要でbreak
parent_index = (current_index - 1)>>1
parent_value = @nodes[parent_index]
break if parent_value <= current_value
# 親より自分が小さいので、入れ替え操作を行う。
# 次のloopのために、current_indexを入れ替えた親のindexに直す
@index[parent_value] = current_index
@nodes[current_index] = parent_value
current_index = parent_index
end
@index[current_value] = current_index
@nodes[current_index] = current_value
end
def delete(delete_target_value)
# 存在しない値ならdeleteできないのでreturn (入力を信じるのであれば、必要無い確認)
return unless @index[delete_target_value]
# 1.削除するのでsizeが減る
# 2.末端は他のnodeと入れ替わるので、末端を削除する
# 3.削除されるnodeのindexも削除する
@size -= 1
current_node_value = @nodes[@size]
@nodes[@size] = nil
current_node_index = @index.delete(delete_target_value) # deleteの返り値は削除した値
# 削除したのがそもそも末端だったら、終了。
return if current_node_index == @size
# 削除したのが末端じゃないなら、末端にある値を削除した場所に持ってくる
@nodes[current_node_index] = current_node_value
@index[current_node_value] = current_node_index
# 大小関係が正されるように、要素を入れ替える
# delete_target = d, last_node = l
# d > l のとき
# d_child > d > l で子は問題ないけど
# d_parent < l < d, l < d_parent < d のどっちかわからなくて、後者だと問題なのでチェックする
# この問題が解決するまで、親方向にチェック & 入れ替えを続ける
if delete_target_value > current_node_value
parent_node_index = (current_node_index - 1) >> 1
while @nodes[parent_node_index]&.> @nodes[current_node_index]
change(parent_node_index, current_node_index)
current_node_index = parent_node_index
current_node_value = @nodes[current_node_index]
parent_node_index = (current_node_index - 1) >> 1
end
# d < l のとき
# d_parent < d < d で親は問題ないけど
# d_child > l > d, l > d_child > d のどっちかわからなくて、後者だと問題なのでチェックする
# この時、(子1,子2,親) の内最小の値を新しい親にする事。
# この問題が解決するまで、子方向にチェック & 入れ替えを続ける
else
while
# 子ノードのindexを取得、小さい方(左)のindexがsize以上だったら、そこに要素は無いはずなのでbreak
child_node_index_r = (current_node_index << 1) + 2
child_node_index_l = child_node_index_r - 1
break unless child_node_index_l < @size
# 子ノードの内小さい方の値と、current_nodeを入れ替えるので、計算。
# 右はnilの可能性があるので、右側のvalueからsafe navigation operatorを使う
# 今のノードの値が、小さい方の子の値よりも小さかったそこでストップ
child_node_value_l = @nodes[child_node_index_l]
child_node_value_r = @nodes[child_node_index_r]
if child_node_value_r&.<child_node_value_l
min_child_value = child_node_value_r
min_child_index = child_node_index_r
else
min_child_value = child_node_value_l
min_child_index = child_node_index_l
end
break if min_child_value > current_node_value
# 入れ替えた後、現在のindexを入れ替え先のindexにして、次のloopへ行く
change(current_node_index, min_child_index)
current_node_index = min_child_index
end
end
end
def top
@size == 0 ? -1 : @nodes[0]
end
# デバッグ用
def check_valid
queue = [0]
while queue.size > 0
i = queue.shift
child_1 = (i + 1) << 1
child_2 = child_1 - 1
if child_2 < @size
if child_1 < @size
queue << child_1
raise if @nodes[child_1] < @nodes[i]
end
queue << child_2
raise if @nodes[child_2] < @nodes[i]
end
end
end
private
def change(index_i, index_j)
@nodes[index_i], @nodes[index_j] = @nodes[index_j], @nodes[index_i]
@index[@nodes[index_i]] = index_i
@index[@nodes[index_j]] = index_j
end
end
initialize(n)
Rubyでnewしたときに呼ばれるメソッドです。
ツリー構造を表すための@nodes(Array)
値からArray上のindexを調べるための@index(Hash)
現在の要素数を示す@sizeがあります。
change(index_i, index_j)
indexでi番目の値とj番目の値を入れ替えます。
@nodesの値を入れ替えたら、それに応じて@indexの値も入れ替えます。
push(current_value)
値を追加します。
上記gif画像を同じような操作を行います(詳細はコードのコメントを参照ください)
すでにある値をpushされたら、何もせずにreturnします
delete(delete_target_value)
値を削除します
上記gif画像を同じような操作を行います(詳細はコードのコメントを参照ください)
存在しない値をdeleteされたら何もせずにreturnします
top
最小値へのアクセスです。
@sizeが0のときは-1を返していますが、
必要であれば適当にもっと小さい値を返しても良いです。
check_valid
デバッグ用に作ったやつです。
親子関係が正しいかチェックしてバグってたらraiseします。
使用例
冒頭の問題の解答です
https://atcoder.jp/contests/abc128/submissions/5916231
SetやSortedSet、sortedなArray(bsearchによる挿入)、どれを試してもTLE(制限時間オーバー)になりました。
solve.rb上のURLから確認できるコードです。長いので閉じておきます。
class Heap
def initialize(n)
@nodes = Array.new(n)
@index = Hash.new
@size = 0
end
def push(current_value)
# 存在する値ならpushしないでreturn (入力を信じるのであれば、必要無い確認)
return if @index[current_value]
# 今から値を入れるのは、@size番目
# 0番目...@size-1までの@size個の要素が元々あるから。
current_index = @size
@size += 1
# 末端に要素を追加した時、その値が小さければ、どんどん親ノードへ上がっていく。
while current_index > 0 do
# 親ノードのindexは (i-1) >> 1 で計算できる
# 親より自分が大きいなら、入れ替え不要でbreak
parent_index = (current_index - 1)>>1
parent_value = @nodes[parent_index]
break if parent_value <= current_value
# 親より自分が小さいので、入れ替え操作を行う。
# 次のloopのために、current_indexを入れ替えた親のindexに直す
@index[parent_value] = current_index
@nodes[current_index] = parent_value
current_index = parent_index
end
@index[current_value] = current_index
@nodes[current_index] = current_value
end
def delete(delete_target_value)
# 存在しない値ならdeleteできないのでreturn (入力を信じるのであれば、必要無い確認)
return unless @index[delete_target_value]
# 1.削除するのでsizeが減る
# 2.末端は他のnodeと入れ替わるので、末端を削除する
# 3.削除されるnodeのindexも削除する
@size -= 1
current_node_value = @nodes[@size]
@nodes[@size] = nil
current_node_index = @index.delete(delete_target_value) # delteの返り値は削除した値
# 削除したのがそもそも末端だったら、終了。
return if current_node_index == @size
# 削除したのが末端じゃないなら、末端にある値を削除した場所に持ってくる
@nodes[current_node_index] = current_node_value
@index[current_node_value] = current_node_index
# 大小関係が正されるように、要素を入れ替える
# delete_target = d, last_node = l
# d > l のとき
# d_child > d > l で子は問題ないけど
# d_parent < l < d, l < d_parent < d のどっちかわからなくて、後者だと問題なのでチェックする
# この問題が解決するまで、親方向にチェック & 入れ替えを続ける
if delete_target_value > current_node_value
parent_node_index = (current_node_index - 1) >> 1
while @nodes[parent_node_index]&.> @nodes[current_node_index]
change(parent_node_index, current_node_index)
current_node_index = parent_node_index
current_node_value = @nodes[current_node_index]
parent_node_index = (current_node_index - 1) >> 1
end
# d < l のとき
# d_parent < d < d で親は問題ないけど
# d_child > l > d, l > d_child > d のどっちかわからなくて、後者だと問題なのでチェックする
# この時、(子1,子2,親) の内最小の値を新しい親にする事。
# この問題が解決するまで、子方向にチェック & 入れ替えを続ける
else
while
# 子ノードのindexを取得、小さい方(左)のindexがsize以上だったら、そこに要素は無いはずなのでbreak
child_node_index_r = (current_node_index << 1) + 2
child_node_index_l = child_node_index_r - 1
break unless child_node_index_l < @size
# 子ノードの内小さい方の値と、current_nodeを入れ替えるので、計算。
# 右はnilの可能性があるので、右側のvalueからsafe navigation operatorを使う
# 今のノードの値が、小さい方の子の値よりも小さかったそこでストップ
child_node_value_l = @nodes[child_node_index_l]
child_node_value_r = @nodes[child_node_index_r]
if child_node_value_r&.<child_node_value_l
min_child_value = child_node_value_r
min_child_index = child_node_index_r
else
min_child_value = child_node_value_l
min_child_index = child_node_index_l
end
break if min_child_value > current_node_value
# 入れ替えた後、現在のindexを入れ替え先のindexにして、次のloopへ行く
change(current_node_index, min_child_index)
current_node_index = min_child_index
end
end
end
def top
@size == 0 ? -1 : @nodes[0]
end
# デバッグ用
def check_valid
queue = [0]
while queue.size > 0
i = queue.shift
child_1 = (i + 1) << 1
child_2 = child_1 - 1
if child_2 < @size
if child_1 < @size
queue << child_1
raise if @nodes[child_1] < @nodes[i]
end
queue << child_2
raise if @nodes[child_2] < @nodes[i]
end
end
end
private
def change(index_i, index_j)
@nodes[index_i], @nodes[index_j] = @nodes[index_j], @nodes[index_i]
@index[@nodes[index_i]] = index_i
@index[@nodes[index_j]] = index_j
end
end
nn, qq = gets.split.map(&:to_i)
events = []
temp = []
1.step(nn, 1) do |_i|
temp = gets.split.map(&:to_i)
next if temp[1] - temp[2] <= 0
x = temp[0] - temp[2]
x = x > 0 ? x : 0
events.push([temp[1] - temp[2], 1, temp[2]])
events.push([temp[0] - temp[2], 0, temp[2]])
end
1.step(qq, 1) do |i|
events.push([gets.to_i, 2, i])
end
events.sort_by!(&:first)
ss = Heap.new(nn)
ans = []
events.each do |event|
if event[1] == 0
ss.push(event[2])
elsif event[1] == 1
ss.delete(event[2])
else
ans[event[2]] = ss.top
end
end
puts ans[1..-1]
最後に
最後までお読みいただきありがとうございました。
要素の削除を伴う場合はheapがめっちゃ強いです。
追加・削除・最小値問い合わせを行いたい場合、
RubyのSetやSortedSetはかなり遅いようです。。。
パフォーマンス比較のbenchmarkは需要があれば記事を書きます。
大小比較を括りだして、
そこだけをカスタマイズすることで辞書順などの推移律が成り立つものに対して、
heapを構成できるようにしたいですね。
親-子の関係がすべての親子で成り立ってればheapになれるはずです。
(そのうちやります)
参考
https://www.codereading.com/algo_and_ds/ds/heap.html
http://www.cs.info.mie-u.ac.jp/~toshi/lectures/algorithm/heap.pdf