概要
自動車の属性データからガソリン1ガロンあたりの走行距離を予測するモデル作成を行います。
データはこちらからダウンロードしてください。
他にも「Learn Python In Seminar」のシリーズとして書いているので、よければご覧ください!
利用するデータの説明
| カラム | ヘッダ名称 | データ型 | 説明 |
|---|---|---|---|
| 1 | mpg | float | ガソリン1ガロンあたりの走行距離 |
| 2 | cylinders | varchar | シリンダー |
| 3 | displacement | float | 排気量 |
| 4 | horsepower | float | 馬力 |
| 5 | weight | float | 重量 |
| 6 | acceleration | float | 加速度 |
| 7 | model year | varchar | 年式 |
| 8 | origin | varchar | 起源 |
| 9 | car name | varchar | 車名 |
ライブラリのインストール
import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error as MSE
from sklearn.linear_model import LinearRegression as LR
データの読み込み
df_train = pd.read_csv('data/train.tsv', sep='\t')
print(df_train.head())
↓
id mpg cylinders displacement horsepower weight acceleration model year origin car name
0 0 29.0 4 135.0 84.00 2525.0 16.0 82 1 dodge aries se
1 3 31.9 4 89.0 71.00 1925.0 14.0 79 2 vw rabbit custom
2 9 19.0 6 156.0 108.0 2930.0 15.5 76 3 toyota mark ii
3 11 28.0 4 90.0 75.00 2125.0 14.5 74 1 dodge colt
4 13 37.7 4 89.0 62.00 2050.0 17.3 81 3 toyota tercel
欠損値の確認
print(df_train.isnull().sum())
↓
id 0
mpg 0
cylinders 0
displacement 0
horsepower 0
weight 0
acceleration 0
model year 0
origin 0
car name 0
dtype: int64
基本統計量
print(df_train.describe(include='all'))
↓
id mpg cylinders displacement horsepower weight acceleration model year origin car name
count 199.000000 199.000000 199.000000 199.000000 199 199.000000 199.000000 199.000000 199.000000 199
unique NaN NaN NaN NaN 71 NaN NaN NaN NaN 167
top NaN NaN NaN NaN 90.00 NaN NaN NaN NaN ford pinto
freq NaN NaN NaN NaN 12 NaN NaN NaN NaN 4
mean 200.170854 24.307035 5.296482 183.311558 NaN 2883.839196 15.647739 76.165829 1.582915 NaN
std 113.432759 7.797665 1.644562 98.400457 NaN 819.766870 2.701885 3.802928 0.798932 NaN
min 0.000000 9.000000 3.000000 71.000000 NaN 1613.000000 8.500000 70.000000 1.000000 NaN
25% 98.500000 18.000000 4.000000 98.000000 NaN 2217.500000 14.000000 73.000000 1.000000 NaN
50% 202.000000 24.000000 4.000000 140.000000 NaN 2702.000000 15.500000 76.000000 1.000000 NaN
75% 294.500000 30.500000 6.000000 250.000000 NaN 3426.500000 17.150000 80.000000 2.000000 NaN
max 396.000000 44.600000 8.000000 454.000000 NaN 5140.000000 23.700000 82.000000 3.000000 NaN
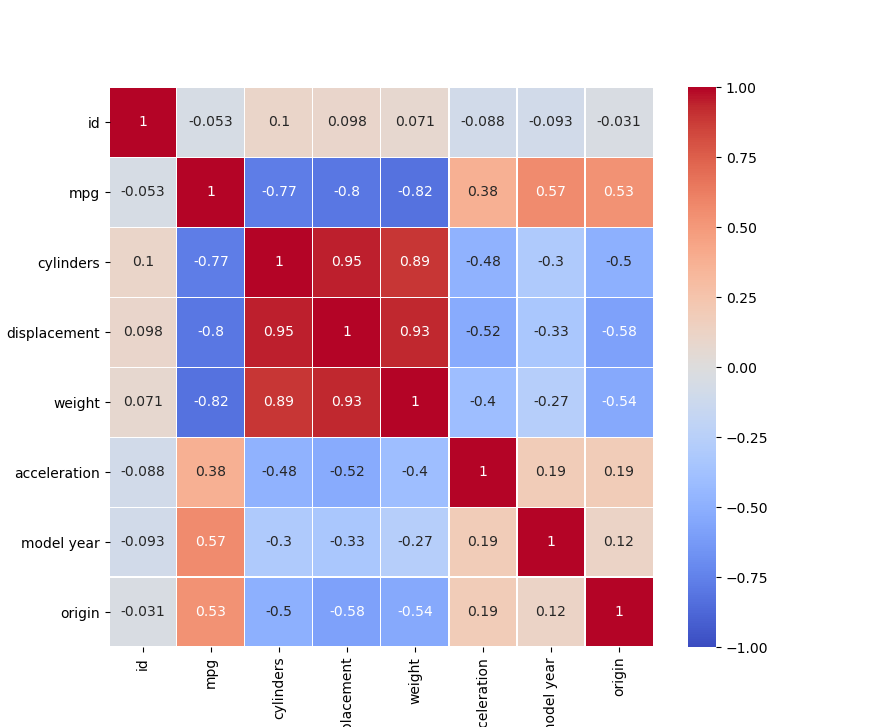
相関係数
print(df_train.corr())
↓
id mpg cylinders displacement weight acceleration model year origin
id 1.000000 -0.052688 0.103419 0.098416 0.070563 -0.087649 -0.093272 -0.031421
mpg -0.052688 1.000000 -0.770160 -0.804635 -0.820660 0.379721 0.568471 0.533671
cylinders 0.103419 -0.770160 1.000000 0.950600 0.893256 -0.479561 -0.303462 -0.497373
displacement 0.098416 -0.804635 0.950600 1.000000 0.933038 -0.523955 -0.329817 -0.579805
weight 0.070563 -0.820660 0.893256 0.933038 1.000000 -0.401757 -0.265562 -0.535893
acceleration -0.087649 0.379721 -0.479561 -0.523955 -0.401757 1.000000 0.194854 0.189193
model year -0.093272 0.568471 -0.303462 -0.329817 -0.265562 0.194854 1.000000 0.124279
origin -0.031421 0.533671 -0.497373 -0.579805 -0.535893 0.189193 0.124279 1.000000
相関係数の可視化
- mpg(ガロンあたりの走行距離)とdisplacement、weightに強い負の相関関係
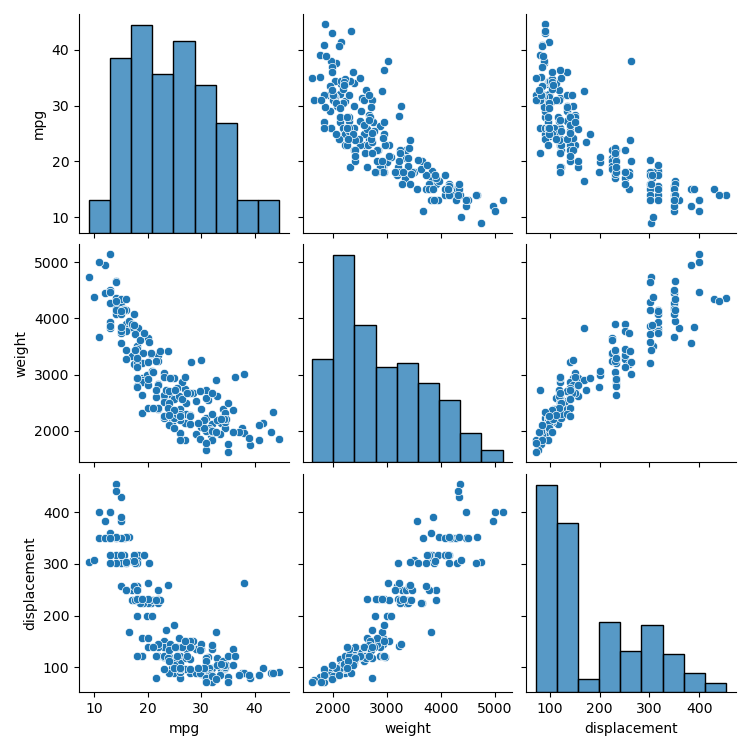
相関関係の可視化
sns.pairplot(df_train[["mpg", "weight", "displacement"]])
↓
重回帰モデルの作成
# データの準備
y_train = df_train[["mpg"]] # 被説明変数
X_train = df_train[["weight", "displacement"]] # 説明変数
# モデルの生成
lr = LR()
# モデルの学習
lr.fit(X_train, y_train)
学習結果
print(lr.coef_) # 傾き
print(lr.intercept_) # 切片
print(lr.score(X_train, y_train)) # 決定係数
↓
[[-0.00513703 - 0.02383218]] # 傾き
[43.4901176] # 切片
0.6851901992035567 # 決定係数
- y = b1 × -0.00513703 + b2 × -0.02383218 + 43.4901176
学習結果と実データの比較
df_train['pred'] = y_pred_train
# 実データと予測結果の差をresとして代入
df_train['res'] = df_train['mpg'] - df_train['pred']
# ソート
print(df_train.sort_values(by='res'))
↓
mpg displacement weight model year car name pred res
19.0 122.0 2310.0 73 ford pinto 28.716052 - 9.716052
20.0 140.0 2408.0 72 chevrolet vega 27.783644 - 7.783644
18.0 121.0 2933.0 72 volvo 145e(sw) 25.539515 - 7.539515
19.0 121.0 2868.0 73 volvo 144ea 25.873422 - 6.873422
21.0 140.0 2401.0 73 chevrolet vega 27.819603 - 6.819603
... ... ... ... ... ... ...
41.5 98.0 2144.0 80 vw rabbit 30.140772 11.359228
43.1 90.0 1985.0 78 volkswagen rabbit custom diesel 31.148217 11.951783
44.6 91.0 1850.0 80 honda civic 1500 gl 31.817884 12.782116
43.4 90.0 2335.0 80 vw dasher(diesel) 29.350257 14.049743
38.0 262.0 3015.0 82 oldsmobile cutlass ciera(diesel) 21.757941 16.242059
- model yearが古い時にマイナス、新しい時にプラスにずれている
- すでにmodel yearとmpgに相関関係が確認
特徴量の追加
説明変数にmodel yearを追加
y_train = df_train[["mpg"]]
X_train = df_train[["weight", "displacement", "model year"]]
lr = LR()
lr.fit(X_train, y_train)
y_pred_train = lr.predict(X_train)
print(lr.score(X_train, y_train))
↓
0.806202914350324
- model yearを説明変数に設定したところ決定変数の値が約0.2上昇
再検証
df_train['pred'] = y_pred_train
df_train['res'] = df_train['mpg'] - df_train['pred']
print(df_train.sort_values(by='res'))
↓
mpg displacement weight model year car name pred res
19.0 122.0 2310.0 73 ford pinto 25.822268 - 6.822268
22.0 232.0 2835.0 82 ford granada l 28.804316 - 6.804316
19.8 200.0 2990.0 79 mercury zephyr 6 25.711137 - 5.911137
21.5 121.0 2600.0 77 bmw 320i 27.049786 - 5.549786
23.5 173.0 2725.0 81 chevrolet citation 29.040204 - 5.540204
... ... ... ... ... ... ...
36.4 121.0 2950.0 80 audi 5000s(diesel) 27.133402 9.266598
44.6 91.0 1850.0 80 honda civic 1500 gl 34.205448 10.394552
38.0 262.0 3015.0 82 oldsmobile cutlass ciera(diesel) 27.517075 10.482925
43.1 90.0 1985.0 78 volkswagen rabbit custom diesel 31.838867 11.261133
43.4 90.0 2335.0 80 vw dasher(diesel) 31.161030 12.238970
- 通常年式だけではなく、車の種類とセットのため、car nameもセットで関係していると予測
ダミー変数化
ダミー変数化できるカラムを自動で認識
X_train = pd.get_dummies(
df_train[["weight", "displacement", "model year", "car name"]])
print(X_train)
↓
weight displacement model year ... car name_vw dasher(diesel) car name_vw rabbit car name_vw rabbit custom
2525.0 135.0 82 ... 0 0 0
1925.0 89.0 79 ... 0 0 1
2930.0 156.0 76 ... 0 0 0
2125.0 90.0 74 ... 0 0 0
2050.0 89.0 81 ... 0 0 0
... ... ... ... ... ... ...
2110.0 85.0 80 ... 0 0 0
3570.0 302.0 78 ... 0 0 0
3433.0 304.0 70 ... 0 0 0
2335.0 90.0 80 ... 1 0 0
2265.0 98.0 73 ... 0 0 0
再度モデルの作成と検証
y_train = df_train[["mpg"]]
X_train = pd.get_dummies(
df_train[["weight", "displacement", "model year", "car name"]])
lr = LR()
lr.fit(X_train, y_train)
y_pred_train = lr.predict(X_train)
df_train['pred'] = y_pred_train
df_train['res'] = df_train['mpg'] - df_train['pred']
print(df_train.sort_values(by='res'))
print(lr.score(X_train, y_train))
↓
mpg displacement weight model year car name pred res
29.0 90.0 1937.0 76 vw rabbit 34.656354 - 5.656354
31.8 85.0 2020.0 79 datsun 210 36.276274 - 4.476274
19.0 122.0 2310.0 73 ford pinto 23.364118 - 4.364118
25.0 116.0 2220.0 76 opel 1900 27.625883 - 2.625883
23.5 173.0 2725.0 81 chevrolet citation 26.067394 - 2.567394
... ... ... ... ... ... ...
28.0 116.0 2123.0 71 opel 1900 25.374117 2.625883
26.5 140.0 2565.0 76 ford pinto 23.871847 2.628153
30.5 97.0 2190.0 77 volkswagen dasher 27.862259 2.637741
40.8 85.0 2110.0 80 datsun 210 36.323726 4.476274
41.5 98.0 2144.0 80 vw rabbit 35.843646 5.656354
0.9834170393004322
- 予測データと実データの差が減少
- car nameのダミー変数化前に比べて決定係数が約0.3上昇
結果
- horsepower、weight、model yearに自動車の走行距離(mpg)に影響
- car nameをダミー変数化することで決定係数が大幅に改善
課題
- car nameを説明変数に入れると未知の車種を予測できなかった(過学習)
→メーカーと車種を分けて分析する必要がある - originやcylindersが未検証
- null以外の欠損値があとで発見