3Dゲーム用の物理エンジンを自作

Last updated at 2024-08-22Posted at 2024-08-21

物理エンジンを自作する

ゲームを作成する際に使用するUnityやUnreal Engineなどゲーム制作ソフトには、物理シミュレーションを行う物理エンジンが普通標準で搭載されている。
これらの物理エンジンを使えば簡単に物体の衝突をシミュレーションしてゲームを作成することができるが、物理エンジンで行っていることを理解し、自分で実装してみたいと興味を持ったので３D空間での物理エンジンを自作してみた。
以下、今回作成した物理エンジンを使った物体の衝突シミュレーションの例である。いずれも３D空間内で物体の反発、回転、摩擦を考慮してシミュレーションしている。

球、直方体、六角柱の物体の衝突

重力のある空間での多数の球の衝突

重力のある空間での多数の三角柱の衝突

重力のある空間での球の運動(1,2,3)

物理エンジンのコードは以下githubにある。

(実行方法)

リポジトリをgit cloneしてディレクトリ直下でnpm install
npm startでブラウザが起動する。画面から実行するシミュレーションを選択する(test-physicsなど)

また、今回自作した物理エンジンを使って簡単なゲームを作成してみた。（昔流行ったスイカゲーム的な、果物を落下させてハイスコアを目指すパズルゲーム）

物理エンジンの仕様

今回作成する物理エンジンで行う物理シミュレーションの内容は以下である。

物体間の衝突による反発は反発係数を元にシミュレーションする
物体間の衝突による回転は衝突座標から受ける力と各物体の重心で慣性モーメントを元にシミュレーションする
物体間の衝突の際の摩擦は垂直方向の力から静止摩擦力、動摩擦力によりシミュレートし、それら摩擦力は物体の速度、回転に影響を及ぼす

各物体の持つ情報は、

位置、回転、スケールが各３次元ベクトルで定義されている
反発係数、静止摩擦係数、動摩擦係数を持つ
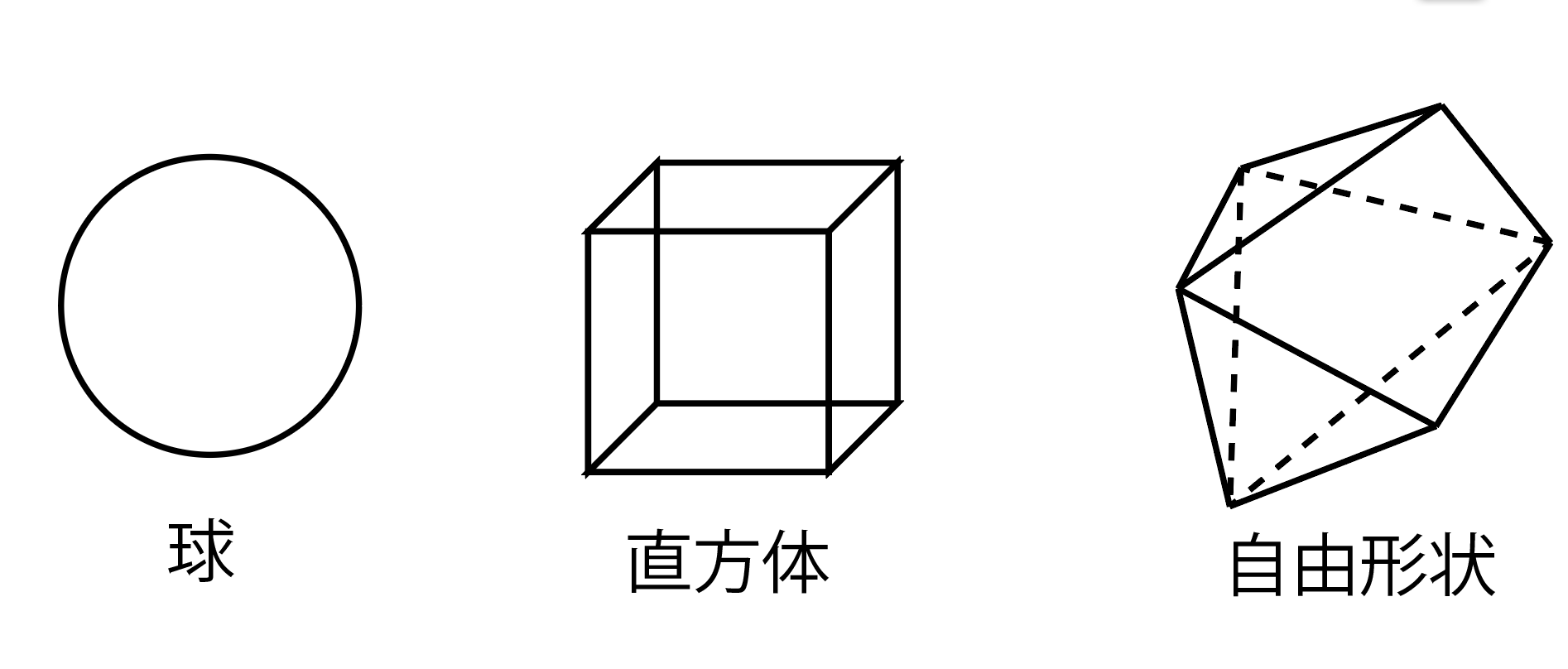
物体の形状(rigid body : 球、直方体、自由形状から選択)が定義されている
xyz方向それぞれで慣性モーメントが定義されている
ものとする。

なお、自由形状とは頂点、辺、面で構成される任意の図形を指す。

実装方法

今回はTypescriptでコードを記述しthreejsを使ってWebGL内の物体の表示を行っている。
物体情報はJSONで定義する。以下は定義例である。

    {
        "name": "targetSphere",
        "type": "primitive",
        "arg": "sphere",
        "initPos": [0,0,0],
        "initRot": [0,0,0],
        "initScale": [1,1,1],
        "physics": {
            "fixed": false,
            "weight": 1,
            "reflectCoef": 0.6,
            "staticFricCoef": 0.5,
            "dynamicFricCoef": 0.4,
            "shape": {
                "type": "sphere",
                "meta": {
                    "offset": [0,0,0],
                    "radius": 1
                }
            },
            "actions": [{
                "type": "push"
            }]
        },
        ...
    }

衝突処理のパイプライン

物体の衝突を判定し、衝突後の物体の位置、速度、回転を計算する際のパイプラインは以下となる。

各物体についてxyz空間に占める領域ボックス(boundary box)を計算する
各物体の領域ボックスから、ぶつかっている可能性がある物体同士を判定する。判定された物体同士のみについて以降の衝突判定を行うことで、無駄な衝突判定の計算を削減できる。なお、ぶつかっている可能性のある物体とはxyz座標全てで領域が重なる部分のある物体同士である
ぶつかっている可能性のある物体について衝突判定を行う
衝突している物体について衝突応答の処理を行い、物体の位置、速度、回転を更新する

以上により物体の衝突シミュレーションを行うことができる。
以降ではぶつかっている可能性のある物体同士について行う衝突判定、衝突応答の詳細について説明する。

各形状同士の衝突判定

各物体同士の衝突はその形状を考慮して衝突後の動作（衝突応答）を計算している。
各形状同士の衝突判定と、衝突座標および衝突相手の物体から受ける抗力の方向の計算方法は以下となる。ただし、直方体と自由形状については衝突判定は全く同じ扱いをしている。これは、２つの形状とも頂点と辺、面で形状が定義されており衝突判定においては直方体は自由形状に含まれるためである。ただ、慣性モーメントの扱いなどの都合上直方体と自由形状を別のものとして扱っている。

球 x 球

球同士の衝突判定は簡単である。球の中心座標を結んだ線の長さが球の半径の和よりも短ければ衝突となる。
衝突座標については球の中心座標を結んだ線を各半径で内分した点となり、衝突方向は相手の球の中心から自身の球の中心の方向となる。

直方体 x 直方体（＝自由形状 x 自由形状、直方体 x 自由形状）

直方体同士の衝突判定については、2段階で判定している。まず、(1)「直方体の各頂点について相手の直方体内に含まれる」かを判定し、次に(2)「直方体の各辺について相手の直方体の各面を貫いている」かを判定することで直方体同士の衝突を判定している。

(1)「直方体の各頂点について相手の直方体内に含まれる」かを判定
すべての頂点について相手の直方体の各面の表側から裏側かを判定する。そして、すべての面で裏側であった場合には頂点が相手の直方体内にあるため衝突と判定する。
(2)「直方体の各辺について相手の直方体の各面を貫いている」かを判定
各辺を構成する２頂点が相手の直方体の各面のそれぞれ表側と裏側にあり、各頂点と面との距離の比で辺を内分した点が面の三角形内に含まれるかを判定し、含まれれば衝突と判定する。

まず計算負荷の低い(1)で判定を行い、衝突していない場合には(2)で再度判定を行う。

球 x 直方体（＝球 x 自由形状）

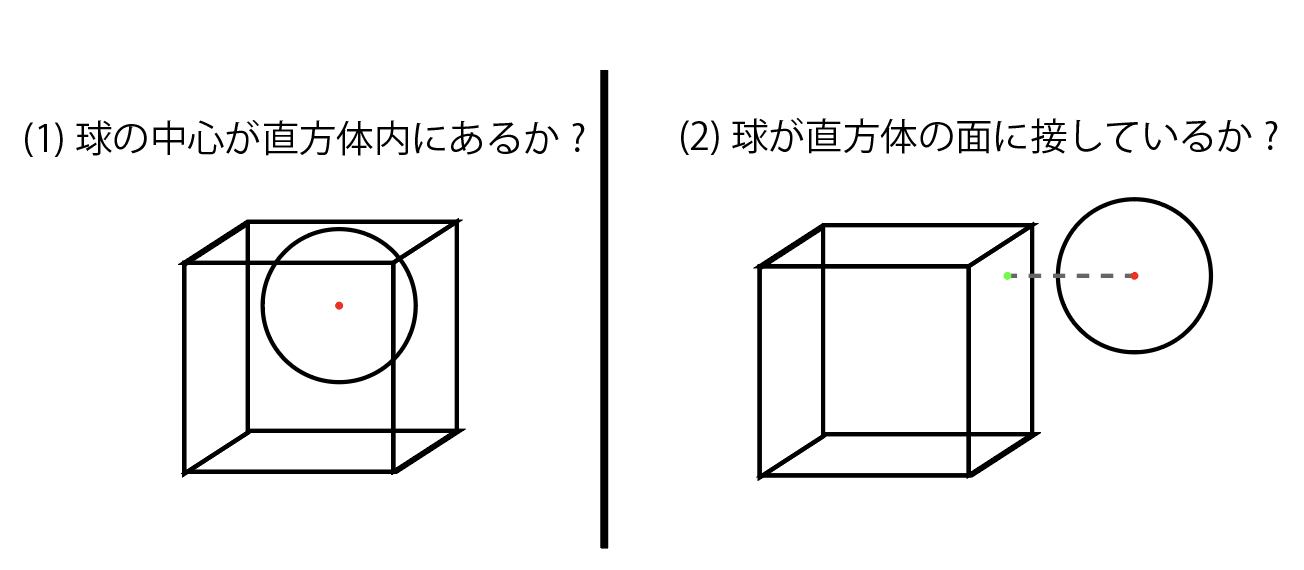
球と直方体の衝突は、(1)「球の中心が直方体内にあるかを判定」し、次に(2)「球が直方体の面に接していることを判定」する。

(1)「球の中心が直方体内にあるかを判定」
球の中心が直方体の全ての面の裏側にあるかを判定すればよい。
(2)「球が直方体の面に接していることを判定」
球の中心から直方体の各面に垂線を下ろす。その垂線の長さが球の半径以下、かつ垂線の足が面内である時、球と直方体は衝突していると判定できる
(3)「球と直方体の辺が接しているかを判定」
球の中心から直方体の各辺に垂線を下ろす。球と直方体の辺の距離、つまり垂線の長さが球の半径以下かを判定する

速度と力の関係

物体の速度変化と加わる力(撃力)の関係は以下運動方程式となる。

m△v = F△t
m:質量、△v:速度変化、F:加わる力の大きさ、△t:力が加わる時間

この式を前提に物体の運動を計算する。ただし、△tについてはあらかじめ物理エンジンのパラメータとして自由に設定できる所与のものとした。
また、実装を簡単にするために一部計算処理を省略している部分もある。

反発の計算

反発は各物体の速度ベクトルを物体の衝突面に対して垂直方向と水平方向に分解し、垂直方向について反発係数を元に衝突後の速度を計算し、物体同士の反発をシミュレーションした。

以下球と直方体が衝突する際のイメージである。球が衝突する時、直方体の衝突面の法線方向を垂直方向として球の速度成分を垂直方向と水平方向に成分分解し、垂直方向の成分(v)に反発係数eを掛ける(eV)。それと水平方向の成分を合成したものが衝突後の速度となる。実際には直方体が静止しているとは限らないため、球の速度は球と直方体の相対速度としている。

例、球同士の反発を計算するコードを抜き出したもの

let posVec = center2.sub(center1)
const posNV = posVec.normal()
const posRatio = (1 - posVec.length() / (radius1 + radius2)) * POS_RATIO
let ratio1 = -posRatio*(weight2/(weight1+weight2))
let ratio2 = posRatio*(weight1/(weight1+weight2))
if(objPhysInfo1.fixed && !objPhysInfo2.fixed) {
    ratio1 = 0
    ratio2 = 1 * posRatio * POS_RATIO
}
if(!objPhysInfo1.fixed && objPhysInfo2.fixed) {
    ratio1 = -1 * posRatio * POS_RATIO
    ratio2 = 0
}
if(objPhysInfo1.fixed && objPhysInfo2.fixed) {
    ratio1 = 0
    ratio2 = 0
}

const posVec1 = posVec.mul(ratio1)
const posVec2 = posVec.mul(ratio2)

const vel1 = velocity1.inner(posNV)
const vel2 = velocity2.inner(posNV)
let newVertVel1 = ( -vel1 + vel2 )*( 1 + reflectCoef )/( weight1 / weight2 + 1 ) + vel1
let newVertVel2 = ( -vel2 + vel1 )*( 1 + reflectCoef )/( weight2 / weight1 + 1 ) + vel2

回転の計算

回転は各物体の重心周りについて衝突した座標から受ける力による回転を計算した。各物体の回転のしにくさは慣性モーメントによって計算で考慮している。なお、衝突の際の力は各物体の相対速度から求めている。

計算方法は、物体の重心から衝突座標を起点とする力のベクトルに対して垂線を下ろす。そして垂線と力のベクトルの外積を計算し、慣性モーメントで割ることで衝突での回転変化の量を求めている。

例、球同士の回転を計算するコードを抜き出したもの

const rotVec1 = rotation1.outer(collisionPos.sub(pos1))
const rotVec2 = rotation2.outer(collisionPos.sub(pos2))

let newRotation1 = rotation1
let newRotation2 = rotation2
const colDiffVel = velocity2.sub(velocity1)
const colDiffVec = posNV.mul(colDiffVel.inner(posNV))
const colPosDistInfo1 = pos1.lineDistVec(collisionPos, collisionPos.add(colDiffVel))
const colPosDistInfo2 = pos2.lineDistVec(collisionPos, collisionPos.add(colDiffVel.mul(-1)))
newRotation1 = colPosDistInfo1.distVec.outer(colDiffVec.mul(-1)).mul(DELTA_TIME).divEach(inertia1)
newRotation2 = colPosDistInfo2.distVec.outer(colDiffVec).mul(DELTA_TIME).divEach(inertia2)

摩擦の計算

摩擦は各物体の速度ベクトルを物体の衝突面に対して垂直方向を垂直抗力とし、水平方向の速度が垂直方向の速度と静止摩擦係数の積より小さい場合には相手の物体と同じ速度になるよう計算し、超える場合には垂直方向の速度と静止摩擦係数の積の一定の力を受けて減速方向に力が加わるようにした。この力により物体の速度、回転が更新される。

例、球同士の摩擦を計算するコードを抜き出したもの

const staticFricCriteria = staticFricCoef * (vertVec1.length() + vertVec2.length())
const fricForce = slipVec1.sub(slipVec2).length()

const colDiffVel = velocity2.sub(velocity1)
const colPosDistInfo1 = center1.lineDistVec(collisionPos, collisionPos.add(colDiffVel))
const colPosDistInfo2 = center2.lineDistVec(collisionPos, collisionPos.add(colDiffVel.mul(-1)))
if(fricForce < staticFricCriteria) {
    const decRatio = fricForce / staticFricCriteria
    const fricRotation1 = colPosDistInfo1.distVec.outer(slipVec1.mul(decRatio)).divEach(inertia1)
    const fricRotation2 = colPosDistInfo2.distVec.outer(slipVec2.mul(decRatio)).divEach(inertia2)
    newRotation1 = fricRotation1
    newRotation2 = fricRotation2
    const fricVelocity1  = newRotation1.outer(collisionPos.sub(pos1)).add(reflectVec1)
    const fricVelocity2  = newRotation2.outer(collisionPos.sub(pos2)).add(reflectVec2)
    newVelocity1 = fricVelocity1
    newVelocity2 = fricVelocity2
} else {
    const subSlipVec1 = slipVec1.mul(dynamicFricCoef)
    const subSlipVec2 = slipVec2.mul(dynamicFricCoef)
    const fricRotation1 = colPosDistInfo1.distVec.outer(subSlipVec1).divEach(inertia1)
    const fricRotation2 = colPosDistInfo2.distVec.outer(subSlipVec2).divEach(inertia2)
    newRotation1 = newRotation1.add(fricRotation1)
    newRotation2 = newRotation2.add(fricRotation2)
    newVelocity1 = newVelocity1.sub(subSlipVec1)
    newVelocity2 = newVelocity2.sub(subSlipVec2)
}

重力、力場、座標軸拘束

物理エンジンには衝突以外にも物体に対して力が加わるような仕組みがある方が便利である。
全ての物体に対して同じ方向の力が加わる重力、球体や直方体内で中心や一定の方向に力が加わる力場、2.5次元ゲームなどで便利な衝突時にxyzで移動方向を拘束する座標軸拘束の機能も実装している。
また、衝突されても片方が動かないような物体の固定もできる。
動作の様子については重力のある空間内での物理シミュレーションの例を参照していただきたい。

まとめ

今回作った物理エンジンは、不完全な部分もあるがそれでもかなり自然な物体同士の衝突運動をシミュレーションできた。
今後はこちらのエンジンを利用し、ゲームの作成などを行なっていきたい。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up