論文のメモ
\2020年のICPRで採択された[On the Evaluation of Generative Adversarial Networks By Discriminative Models]という論文を読んだので、自分なりの解釈をメモとしてまとめる。
ところで、GAN(Generative Adversarial Networks)に対する評価方法は今までいくらでもあったが、それらは1つのタスク(droppingなど)・dmain(画像など)に偏った測定になっている。そこで、既存の方法の弱点を克服する(多くのタスクに共通して使える)評価方法を提案することが本論文の主旨。
1. Introduction
GANの量的評価は難しい。いままで多くの評価手法が提案されてきたがすべて画像認識の領域であり、自然言語などの他の領域ではその手法は有効性を示さない。
本論文では、GANのdiscrinetive modelをSNNs(Siamese Neural Networks)に置き換えてGANを推定する。
また、この論文では以下の三つの成功を挙げている。
- GANに対する賢い評価手法の導入
- 既存の評価手法と比較して、本手法がどのように優れているか説明
- 本手法が、画像認識など7の領域にとどまることなく友好的に使える手法であることの説明
2. Related works
以下は、今までに提案された評価手法である。
IS(Inception Score)
評価の手法は、画像の領域で人間の評価方法に近いが、応用の際に不十分さや間違った評価をしてしまうかの性がある。
そして、最も重要なこの手法の弱点は、画像の良識においてのみの評価でありテキストなどほかの領域においての評価には対応していないことである。詳しくは、Improved Techniques for Training GANsを参照。
FID(Frechet Inception Distance)
ISの弱点を修正するものとして提案された手法。
詳しくはGANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibriumを参照。
これらの手法は、ある領域のデータ・目的とするタスクのみに対応する手法であるので、評価の一般化という点で様々な問題が生じる。(droppingなど)
くどくなるがここでの目標は、これらのことを解決するために、SNNを導入しdomain-agnostic metrics(領域にとらわれないという意味)の導入である。
次章から、提案手法の解説に入る。
3. Proposed Approach
人間は「赤くて丸いからそれはリンゴ」のように多くの概念をもとにしてパターン認識を頭の中で行う。そうすると、その認識の精度について概念からどれくらいずれているかを図ることで達成することが出来る。
しかし、生成データに関するラベルや生成された確率分布などの概念が未知であるGANにとってはこの評価というものは難しい。よって、本物のデータが暗に従っている分布を使って、生成データに隠されている特徴を引き出したい。
提案手法として、GANのdescriminatorをSNNを用いて学習し、最終目標であるGANがどのくらい良く働いているかの評価にもこの学習済みモデルを再活用する。
3.1 SNNの構造
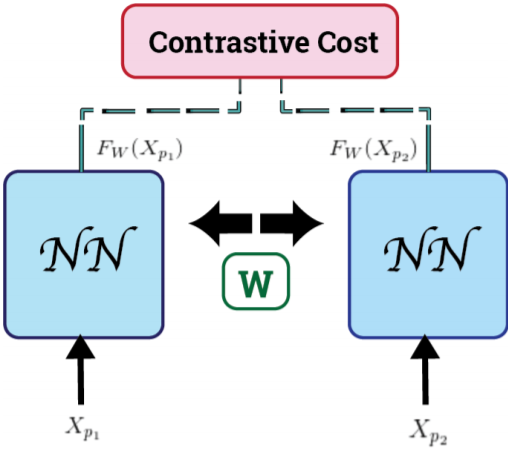
上のように、SNNは二つのNN(ニューラルネットワーク)で構成される。
考え方は単純で、まず二つのサンプルを取ってきて、それらのサンプルが同じクラスに分類されていれば特徴空間における距離を小さくし、別々のクラスに分類されていれば距離は遠くなるように学習(パラメータを更新)するというもの。
ここで、上の図を使って例を示すと、$X_{p_1}$と$X_{p_2}$を訓練データ(テストデータ)からのサンプルとすると、この二つはそれぞれ同じNNを通り(構造もweightもすべて同じ)$F_w(X_{p_1})$と$F_w(X_{p_2})$を出力する。これは出力空間上へのマッピングのようなもの。
ここで、$X_{p_1}$と$X_{p_2}$の距離を以下のように定義する。
D_w(X_{p_1}, X_{p_2}) = ||F_w(X_{p_1})-F_w(X_{p_2})||_2
3.2 損失関数の導入
ここでまず入力は以下のようになる。
二つのサンプルが同じクラスなら、
(X_{p_1},X_{p_2})| X_{p_1},X_{p_2} \in y_i
異なるクラスなら、
(X_{p_1},X_{p_2})| X_{p_1} \in y_i ,X_{p_2} \in y_j, i \ne j
また$Y$は、二つのサンプルが同じクラスであれば+1, 違うクラスであれば-1を取るとすると、損失関数は
\mathcal{L}_w = \frac{1}{\mathcal{N}}\sum_{k=1}^{\mathcal{N}}L_w(Y_i,(X_{p_1},X_{p_2})_i)
となる。
ここで、$\mathcal{N}$は学習に使われるサンプルの個数であり、$L_w(Y_i,(X_{p_1},X_{p_2})_i)$は、
\begin{split}
L_w(Y_i,(X_{p_1},X_{p_2})_k) = Y_i * \mathcal{L}_{gen}&(D_w(X_{p_1},X_{p_2})_k) \\
&+ (1-Y_i)* \mathcal{L}_{imp}(D_w(X_{p_1},X_{p_2})_k)
\end{split} \tag{1}
である。$k$はk番目の二つのサンプルであるということで、genとimpは同じクラス、異なるクラスといことを表している。つまり、クロスエントロピーのようなもので二つのサンプルは同じクラスだったら、Yが1なので(1)の二項目を無視、逆も言えるということになる。
さらに$\mathcal{L}_{gen}$と$\mathcal{L}_{imp}$を以下のように同じクラスか異なるクラスで変えている。(Mは定数)
\begin{split}
&\mathcal{L}_{gen}(D_w) = \frac{1}{2}(D_w)^2 \\
&\mathcal{L}_{gen}(D_w) = \frac{1}{2}(max\{0,M-D_w\})^2
\end{split} \tag{2}
3.3 この手法の利点
構造、weightの同じNNを使うこと、損失関数に以上のものを使う利点は以下である。
1. 出力空間において似ているサンプルが近くなるようにマッピングされる。
2. クラス内の差異を最小にするようにモデルは更新されるので、クラス内の変化にロバスト
3. 出力空間において似ていないサンプルは離れるようにマッピングされる。
4. クラス間の差異を最大にするようにモデルは更新されるので、クラス間の類似性にロバスト
つまり、理想的なクラスタリングが実現されるということを表している。
この利点は、現実問題で以下のようなことを可能にする。
1. GANのfake sampleがどのクラスに属しているかがわかる
2. fake sampleがreal sampleにどれだけ似ているかがわかる(fake sampleの質)
3. 生成されたfake sampleの多様性についてわかる
3.4 評価指標の導入
本論文で提案されている新しい評価指標はSDS(Siamese Distance Score)である。
以下、このスコアの導出方法を順を追ってみていく。
1 N個の全real sample$X^r$をNNに与え、特徴ベクトル
\mathcal{F}_i^r = F_W(X_i^r), i \in {1,...,N}
を計算する。
2 M個の全fake sample$X^s$を同じNNに与え、特徴ベクトル
\mathcal{F}_j^s = F_W(X_j^s), j \in {1,...,M}
を計算する。
3 j番目のfake sampleとすべてのreal sampleとのユークリッド距離を計算する。
\mathcal{D}_i^j = ||\mathcal{F}_j^s - \mathcal{F}_i^r||, i \in {1,...N}
そして、この$\mathcal{D}_i^j$のうち距離が小さいものK個を取ってくる。その、距離の集合を$\mathcal{P}$とする。
4 この集合にあるK個の距離に対応するK個のreal sampleを抽出する。
\mathcal{D}_{\mathcal{P}}^j \rightarrow \mathcal{F}_r^{\mathcal{P}} \rightarrow \mathcal{X}_r^{\mathcal{P}}, |\mathcal{P}| = K, \mathcal{P} \in {1,...,N}
5 4で抽出したreal sampleのラベルから多数決によって選ばれるクラス番号をj番目のfake sample$X_j^s$に付与する。
6 K個のreal sampleから手順5で決定したfake sampleのクラス(C)と同じものR個のreal sampleだけを抽出する。
X_r^R, y(X_r^R) = C
7 j番目のfake sampleに対するSDSを以下のように定義する。
SDS_j = \frac{1}{R}\sum_{p=1}^R ||\mathcal{F}_s^j - \mathcal{F}_r^p||
最終的なSDSは、
SDS = \frac{1}{M}\sum_{q=1}^{M} SDS_q
と計算される。