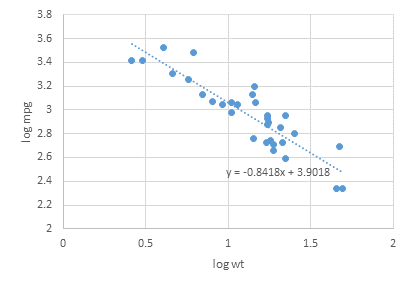
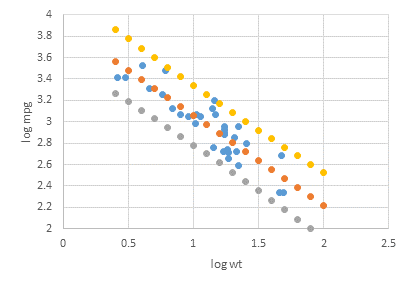
Excelで散布図を描くと、簡単に線形近似線を追加でき、数式まで表示することができるので大変便利です。
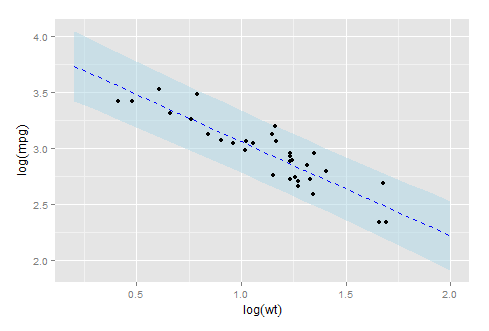
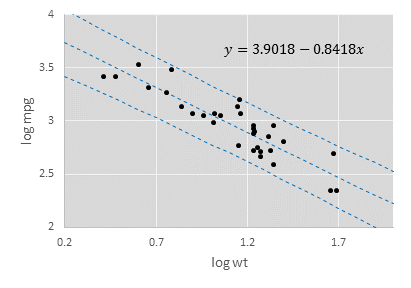
しかし、下図のようにYの予測上限と下限を描きたいとき、Excelではどうやればいいのでしょうか。調べてみると意外と難しくWeb上の情報も少ないようだったので紹介します。
問題設定
新しく開発する自動車の重量wtから燃費mpgを予測したいとします。今回は説明変数が1つしかない簡単な場合です。
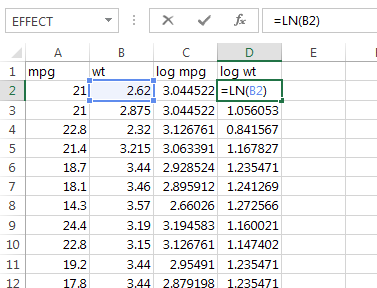
予測に使う自動車データをセルに入力します。セルA2:A33に燃費mpg、B2:B33に重量wtのデータがそれぞれ入力されています。今回は対数変換してから回帰することにします。mpgとwtの対数をC2:C33、D2:D33にそれぞれLN()関数で計算しておきます。
分析ツールで回帰分析をする
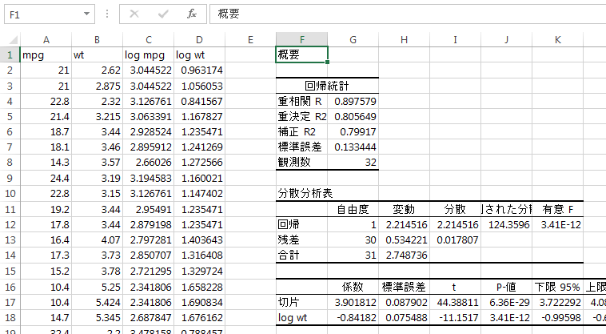
分析ツールの回帰分析で「入力 Y 範囲」に$C$1:$C$33、「入力 X 範囲」に$D$1:$D$33をそれぞれ指定します。「出力先」は$F$1を指定することにします。
ここまでは特に問題ないと思います。
区間予測の計算式
分析ツールは予測値および予測区間を出力してくれないので、自力で予測区間を計算します。新しく開発する自動車の重量wtが$x_0$であるとき、燃費mpgの値$y_0$は以下の95%信頼区間で予測されます。
$$
SE = \sqrt{\left(1 + \frac{1}{n} + \frac{(x_0 - \bar{x})^2}{\sum_{i=1}^n(x_i - \bar{x})^2}\right)V_e}
$$
$$
\hat{y_0} - t_{n-p-1}\left(\frac{1+0.95}{2}\right) SE \le y_0 \le \hat{y_0} + t_{n-p-1}\left(\frac{1+0.95}{2}\right) SE
$$
数式を見たら全部理解できた方 ⇒ これ以上、この記事を読んでいただかなくて結構です。
数式を見たら理解できないと感じた方 ⇒ わからなくても計算できるように説明しますので、この節は飛ばしてください。
数式を見たほうが理解しやすそうという方 ⇒ 少し補足します。
- $SE$は標準誤差です。予測値のばらつきを表す標準偏差みたいなものです。
- $\hat{y_0}$は$y_0$の点予測値です。$\hat{y_0} = 切片 + 傾き \times x_0$で計算できます。
- $\bar{x}$は説明変数$x$の標本平均です。予測に使う自動車データの重量
wtの平均になります。 - $V_e$は残差の分散です。燃費
mpgは重量wtだけでは説明できない個体差があります。個体差のばらつき具合を表します。 - $t_{n-p-1}((1+0.95)/2)$は自由度$n-p-1$のt分布の$(1+0.95)/2$パーセンタイルです。$n$は標本数(観測数)、$p$は説明変数の数です。
セルに予測区間を計算する
セルP2に新しく開発しようとしている自動車の重量wtを入力します。たとえば0.2と入力します。
セルQ2に燃費mpgの点予測値を計算します。=$G$17+$G$18*$P2と入力します。$G$17には分析ツールで求められた切片、$G$18には傾きが入力されています。
セルR2に標準誤差を計算します。=SQRT((1+1/$G$8+($P2-AVERAGE($D$2:$D$33))^2/DEVSQ($D$2:$D$33))*$I$13)と入力します。$G$8は観測数、AVERAGE($D$2:$D$33)は説明変数の標本平均、DEVSQ($D$2:$D$33)は説明変数の偏差平方和、$I$13は残差の分散です。
セルS2とT2に信頼区間の下限、上限を計算します。S2に=$Q2-T.INV((1+0.95)/2,$G$8-$G$12-1)*$R2、T2に=$Q2+T.INV((1+0.95)/2,$G$8-$G$12-1)*$R2と入力します。$G$8は観測数、$G$12は説明変数の数です。
wtの値として0.2だけではなく様々な値を想定しそれぞれの予測区間を計算します。セルP2:P20に想定されうるwtの値として0.2から2.0まで0.1刻みで入力します。Q2:T2を選択してQ20:T20までドラッグして数式をコピーします。
なお、今回は説明変数が1つの単回帰分析ですが、説明変数が2つ以上ある重回帰分析の場合は、計算がもっと複雑になります。あらためて別の機会に紹介したいと思います。
散布図の作成
散布図に点予測値および95%予測上限・下限を追加したところです。
書式調整してこんな感じにしてみました。
Rの場合
参考までにRのコードを載せておきます。Excelでやるよりも簡単です。
library(ggplot2)
data(mtcars)
fit <- lm(log(mpg) ~ log(wt), data = mtcars)
new.wt <- seq(0.2, 2, 0.1)
predicted <- predict(fit, newdata = list(wt = exp(new.wt)), interval = "predict")
predicted <- cbind(as.data.frame(predicted), wt = new.wt)
ggplot(predicted, aes(x= wt)) +
geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "lightblue", alpha = 0.5) +
geom_line(aes(y = fit), color = "blue", linetype = 2) +
geom_point(data = mtcars, aes(x = log(wt), y = log(mpg))) +
xlab(expression(log(wt))) + ylab(expression(log(mpg)))