「Rで学ぶベイズ統計学入門」の例題を紹介するシリーズです。今回は害虫駆除の話をテーマに、モデルの設定から、MCMC実装、結果の要約までの各ステップを細かめにやってみます。
問題
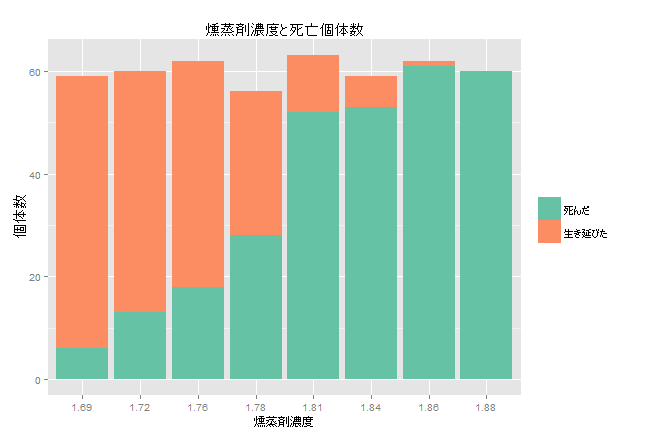
コクヌストモドキの成虫をさまざまなレベルの二硫化炭素ガスに5時間曝露させた後の死亡数を記録したところ以下の通りだった。実験結果をもとに、二硫化炭酸ガスの殺虫効果をモデル化せよ。
| ガス濃度 $w_i$ | 個体数 $n_i$ | 死亡数 $y_i$ |
|---|---|---|
| 1.6907 | 59 | 6 |
| 1.7242 | 60 | 13 |
| 1.7552 | 62 | 18 |
| 1.7842 | 56 | 28 |
| 1.8113 | 63 | 52 |
| 1.8369 | 59 | 53 |
| 1.8610 | 62 | 61 |
| 1.8839 | 60 | 60 |
コクヌストモドキについてはググってみるとショッキングな画像がたくさん出てきます。毒があったり病気を媒介したりという悪さはしないようですが、見た目ゆえに害虫扱いされてしまっている生き物なのかもしれません。
英語ではflour beatleと呼ばれるように、小麦や米などの穀物類を好み、製粉工場などによく発生するそうです。こういう食品工場では害虫駆除のために燻蒸を行うのですが、燻蒸剤は低濃度であっても小麦など主食として毎日口にするものなので、長期反復して摂取すると人体にも影響がでる可能性があります。そこで、殺虫効果が得られる最低限の濃度はどのあたりかを調べるために実験したという背景なのだと、勝手に想像しています。
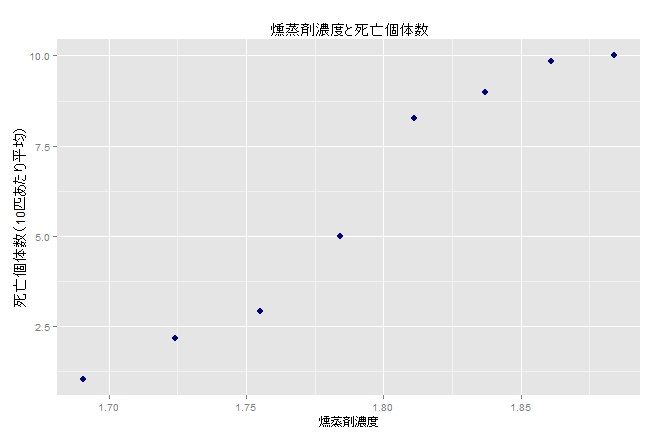
普通のロジスティック回帰でもいけそうに見えますが、今回は少しだけひねったモデルを使います。
モデルを設定する
$事後分布 \propto 尤度 \times 事前分布$というベイズの定理にしたがって、尤度、事前分布を設定し、事後分布を導きます。数式が続きますがご容赦を。
尤度
「$n$匹中$y$匹死亡して$n-y$匹生存した」という問題なので、死亡数$y_i$は二項分布$B(n_i, p_i)$にしたがいます。
$$
L(p_i) \propto \prod_{i=1}^{8} p_i^{y_i} (1-p_i)^{n_i - y_i}
$$
ただし、先ほどグラフで確認したように、死亡する確率$p_i$は燻蒸剤の濃度$w_i$によって変わります。$w_i$と$p_i$の関係は$\mu, ~ \sigma, ~ m_1$というパラメータを使用して次のように与えられると考えることにします。
$$
p_i = \frac{1}{(1 + \exp(-\frac{w_i - \mu}{\sigma})) ^ {m_1}}
$$
$\mu, ~ \sigma, ~ m_1$は観測できない未知の値なので、これら3つのパラメータを推定せよ、というのが今回のゴールになります。
ところで上の式、$1 ~ / ~ (1+\exp(-x))$というおなじみのロジスティック関数によく似ていますが、分母に$m_1$という指数がついています。これは**一般化ロジスティック関数1**と呼ばれる関数の1つの形で、S字カーブが左右対称でない場合にもフィットさせることができるようです。$m_1=1$のときは普通のロジスティック曲線になり、それ以外では左右非対称のS字カーブになります。$m_1$が負の値になると$p_i$が1を越えてしまうので$m_1>0$の実数です。覚えておいたら使える機会あるかも。
事前分布
$\mu, ~ \sigma, ~ m_1$の事前分布を設定します。
- $\mu$については何も情報がないので無限区間の一様分布を仮定します。
- $\sigma$は標準的な無情報事前分布の$1/\sigma$を仮定します。
- $m_1$は「ある程度1に近い数字になるだろう」とあたりをつけて、平均が1になるようなガンマ分布にしたがうと仮定します。
$$
\begin{align*}
p(\mu) &\propto 定数 \newline
p(\sigma) &\propto \frac{1}{\sigma} \newline
p(m_1) &\propto m_1^{a_0-1} \exp\left(-\frac{m_1}{b_0}\right)
\end{align*}
$$
今回は$\mu, ~ \sigma, ~ m_1$は互いに独立と仮定します。同時事前分布は各パラメータの分布を単純に掛け合わせればOKです。
$$
p(\mu, \sigma, m_1) \propto m_1^{a_0-1} \exp\left(-\frac{m_1}{b_0}\right) \frac{1}{\sigma}
$$
なお、$p(m_1)$の右側に出てくる$a_0$と$b_0$はガンマ分布の形を決めるハイパーパラメータですが、今回は天下り的に$a_0 = 0.25, ~ b_0 = 4$を与えることにします。$m_1$の事前平均は$a_0 b_0 = 1$、標準偏差は$\sqrt{a_0 b_0^2} = 2$になります。
事後分布
$事後分布 \propto 尤度 \times 事前分布$ にしたがって、尤度と事前分布より事後分布が導き出されます。
$$
p(\mu, \sigma, m_1 \vert data) \propto m_1^{a_0-1} \exp\left(-\frac{m_1}{b_0}\right) \frac{1}{\sigma} \prod_{i=1}^{8} p_i^{y_i} (1-p_i)^{n_i - y_i}
$$
ここで、$\theta_1 = \mu, ~~ \theta_2 = \log(\sigma), ~~ \theta_3 = \log(m_1) ~$と変数変換を行います。$\sigma$および$m_1$はゼロより大きい実数を想定していますが、対数変換することで任意の実数をとることができるようになり、パラメータ推定が安定します。
$$
p(\theta_1, \theta_2, \theta_3 \vert data) \propto \exp(a_0 \theta_3 -\frac{\exp\theta_3}{b_0}) \prod_{i=1}^{8} p_i^{y_i} (1 - p_i) ^ {n_i - y_i}
$$
対数事後分布は以下のようになります。
$$
\log p(\theta_1, \theta_2, \theta_3 \vert data) \propto a_0 \theta_3 -\frac{\exp\theta_3}{b_0} + \sum_{i=1}^{8} y_i \log p_i + (n_i - y_i) \log(1 - p_i)
$$
以上で事後分布の確率密度関数が求められました。Rで対数事後分布を実装してみましょう。
# データ
dat <- data.frame(
w = c(1.6907, 1.7242, 1.7552, 1.7842, 1.8113, 1.8369, 1.8610, 1.8839),
n = c(59, 60, 62, 56, 63, 59, 62, 60),
y = c(6, 13, 18, 28, 52, 53, 61, 60)
)
# ハイパーパラメータ
hyp.par <- list(a0 = 0.25, b0 = 4)
# 対数事後分布
logpost <- (function(w, y, n, a0, b0) {
force(c(w, y, n, a0, b0))
# データとハイパーパラメータをバインドした関数を返す
function(theta) {
x <- (w - theta[1]) / exp(theta[2])
p <- 1 / (1 + exp(-x)) ^ exp(theta[3])
a0 * theta[3] - exp(theta[3]) / b0 + sum(y * log(p) + (n - y) * log(1 - p))
}
})(dat$w, dat$y, dat$n, hyp.par$a0, hyp.par$b0)
MCMCを実装する
事後分布の関数が定義できたので、MCMCでサンプリングをします。
上で求めた事後分布は、「○○分布」というような名前のついていない、まったく新しい未知の確率分布です。したがって、平均やパーセンタイルや標準偏差といった統計量は不明です。このような場合は、MCMCというアルゴリズム群を利用して、この新種の「名無し分布」にしたがうランダムサンプルを発生させ、ランダムサンプルの平均やパーセンタイルなどをもって事後分布の推定値とする、というのが一般的なアプローチです。
今回はstanやBUGSなどのツールは使わず、あえて一からRで実装して茨の道を行きたいと思います。MCMCの中でもっとも単純なM-H法というアルゴリズムを実装してみます。世の中に分かりやすい解説がありあまるほどにあるので、説明は省略してさっそくコードです。
mh <- function(logpost, start, n.iter,
var = diag(length(start)), scale = 1) {
# パラメータ数
pb <- length(start)
# サンプルを保存する行列
Mpar <- array(0, dim = c(n.iter, pb))
# 提案分布の共分散行列のコレスキー分解 => 多変量正規分布のランダムサンプルに使用
a <- chol(var)
# 多変量正規分布のランダムサンプルを生成する関数
proposal <- function(b) b + scale * t(a) %*% array(rnorm(pb), c(pb, 1))
# 初期値
b <- matrix(t(start))
# 初期値の対数密度
lb <- logpost(as.numeric(b))
for(i in 1:n.iter) {
# 次のサンプルの候補値
bc <- proposal(b)
# 候補値の対数密度
lbc <- logpost(t(bc))
# 現在値と候補値の密度の比
prob <- exp(lbc - lb)
if (!is.na(prob)) {
# 候補値を受理するかどうか決める
if(runif(1) < prob) {
lb <- lbc
b <- bc
}
}
Mpar[i, ] <- b
}
colnames(Mpar) <- names(start)
Mpar
}
この関数は5つの引数をとります。
-
logpostは先ほど実装した対数事後分布です。 -
startはサンプルの初期値を指定します。 -
n.iterはイタレーション回数(サンプルの個数)を指定します。 -
varは提案分布(多変量正規分布)の分散共分散行列を指定します。 -
scaleは次の候補値にジャンプする幅をコントロールします。
MCMCサンプルを抽出する
実装したMCMCアルゴリズムを使って事後分布のサンプルを抽出したいと思います。
ここで難しいのが、初期値startと、提案分布の分散共分散行列varをどうやって指定するかです。これらのパラメータを適切に指定しないと、場合によってはうまく1つの値に収束しなかったり、発散したりしてしまいます。
「Rで学ぶベイズ統計学入門」で紹介されているアプローチは、ラプラス近似によるモードと分散共分散行列を利用するものです。つまり、事後分布を多変量正規分布で近似したときのモードおよび分散共分散行列を提案分布として利用します。
# ラプラス近似のモードと分散共分散行列
theta <- c(1.78, -3.8, 0)
fit <- optim(theta, logpost, control = list(fnscale = -1),
hessian = TRUE)
fit.laplace <- list(mode = fit$par, var = -solve(fit$hessian))
names(fit.laplace$mode) <- c("theta_1", "theta_2", "theta_3")
fit.laplace
# $mode
# theta_1 theta_2 theta_3
# 1.817287 -4.140253 -1.246698
#
# $var
# [,1] [,2] [,3]
# [1,] 0.0001245104 -0.002338171 -0.004135352
# [2,] -0.0023381708 0.066849750 0.096206886
# [3,] -0.0041353520 0.096206886 0.158709740
これらの値を利用して実際にMCMCサンプリングを実行してみます。
# MCMCで10000個のサンプルを抽出
start <- fit.laplace$mode
var <- fit.laplace$var
fit.mcmc <- mh(logpost, start, 10000, var, scale = 2)
# 各変数を変換前の変数に戻す
fit.mcmc[, 1] <- fit.mcmc[, "theta_1"]
fit.mcmc[, 2] <- exp(fit.mcmc[, "theta_2"])
fit.mcmc[, 3] <- exp(fit.mcmc[, "theta_3"])
colnames(fit.mcmc) <- c("mu", "sigma", "m1")
head(fit.mcmc)
# mu sigma m1
# [1,] 1.817287 0.01591882 0.2874523
# [2,] 1.817287 0.01591882 0.2874523
# [3,] 1.817287 0.01591882 0.2874523
# [4,] 1.810314 0.01959122 0.4171682
# [5,] 1.805867 0.02203263 0.5931154
# [6,] 1.805867 0.02203263 0.5931154
こんな感じに事後分布のサンプルが取得できました。数値計算に関しては「Rは遅い」というイメージがありますが、3つのパラメータを各10000個ぐらいであれば意外と驚くほど一瞬でした。
結果の要約と図示にはcodaパッケージというお手軽ツールがあるので、手を抜いて使うことにします。
library(coda)
# mcmcオブジェクトに変換
fit.mcmc <- mcmc(fit.mcmc)
summary(fit.mcmc)
#
# Iterations = 1:10000
# Thinning interval = 1
# Number of chains = 1
# Sample size per chain = 10000
#
# 1. Empirical mean and standard deviation for each variable,
# plus standard error of the mean:
#
# Mean SD Naive SE Time-series SE
# mu 1.81588 0.014333 1.433e-04 0.0006479
# sigma 0.01648 0.004945 4.945e-05 0.0002131
# m1 0.32260 0.178934 1.789e-03 0.0088673
#
# 2. Quantiles for each variable:
#
# 2.5% 25% 50% 75% 97.5%
# mu 1.783659 1.80812 1.81755 1.82553 1.83948
# sigma 0.008128 0.01309 0.01592 0.01948 0.02712
# m1 0.108049 0.21104 0.28345 0.39449 0.75301
#
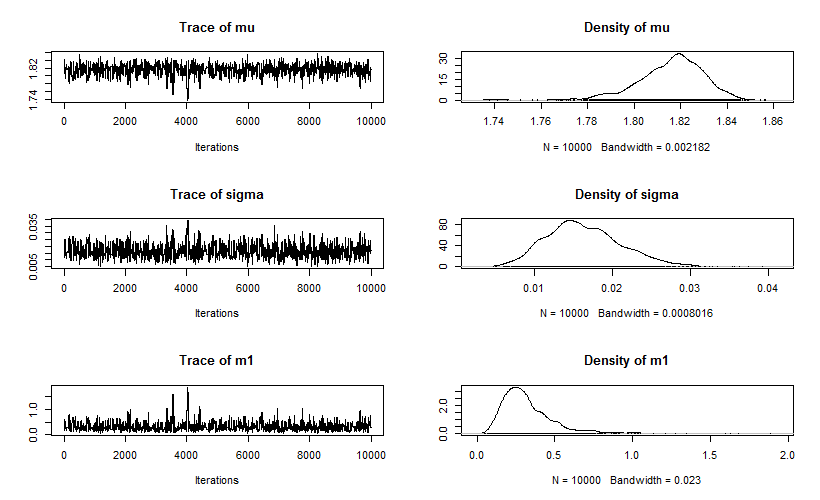
plot(fit.mcmc)
トレースは少し極端な値に飛んでいる部分もありますが、だいたい定常になっているようです。$\sigma$と$m_1$の収束はあまり良くないように見えますが、データが少ないので仕方ないのかもしれません。
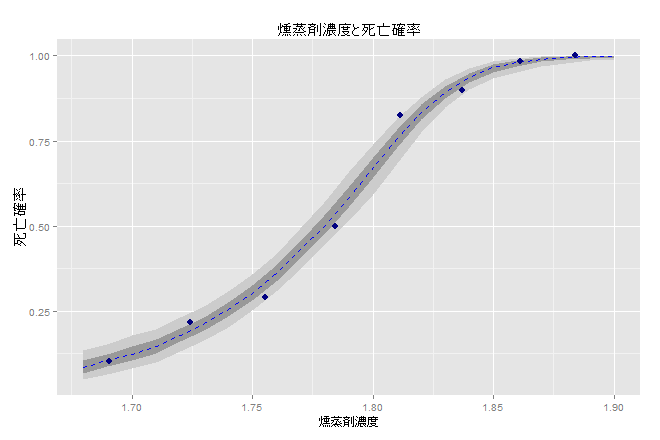
最後に、虫さんが死亡する確率の信用区間を数値計算してみます。観測された死亡割合とあわせてプロットしてみたグラフも載せておきます。
ci <- sapply(dat$w, function(w) {
theta <- fit.mcmc[sample(1:nrow(fit.mcmc), 1000, replace = TRUE), ]
p <- apply(theta, 1, function(theta) {
1 / (1 + exp(-(w - theta[1]) / theta[2])) ^ theta[3]
})
c(w = w, quantile(p, probs = c(0.05, 0.25, 0.5, 0.75, 0.95)))
})
as.data.frame(t(ci))
# w 5% 25% 50% 75% 95%
# 1 1.6907 0.05740753 0.08706287 0.1047644 0.1233634 0.1554516
# 2 1.7242 0.14613715 0.17240949 0.1903245 0.2143951 0.2457606
# 3 1.7552 0.28218688 0.31250430 0.3318577 0.3571403 0.3861808
# 4 1.7842 0.47056689 0.50749401 0.5341140 0.5648077 0.6071070
# 5 1.8113 0.69490929 0.74010709 0.7685029 0.7945641 0.8253288
# 6 1.8369 0.88723010 0.90937576 0.9253902 0.9389310 0.9550584
# 7 1.8610 0.95787142 0.97199247 0.9815069 0.9884894 0.9944301
# 8 1.8839 0.98182148 0.99144663 0.9955730 0.9979981 0.9994443
まとめ
今回は二項分布にしたがうデータの確率を一般化ロジットモデルを使って分析してみました。MCMCを使うことでかなり良さげな精度でパラメータを推定することができました。
やってみて一番難しいと感じたのは、MCMCの初期値と提案分布の決め方です。今回は非常にシンプルなモデルだったので、ある程度このあたりに収束しそうだという数字がわかっていましたが、パラメータが増えたり階層的になったりしてより複雑なモデルになった場合、今回のようなやり方は難しいと思うので、どうすればいいのか今後勉強したいと思います。
参考文献
-
英語Wikipedia: Generalized logistic functionぐらいしか詳しい情報が見つからず・・・ ↩