はじめに
皆様、Merry Christmasでございます。
カレンダーの空きがあまりなかったので、僭越ながらラスト直前の記事を書かせていただきます。
何の話を書こうか、何の話が書けるかを考えていましたが、プログラムの計算量の話とかあまりしないですよね。たまには思い出したくなったのでこの機会に久々に思い出したいと思います。
あまり役には立たないかもしれないけど、きっと役に立つのかもしれない、そんな内容になっていればいいと思います。
計算理論において、問題を解くための時間や資源を計算して、複雑さを事前に調べることは重要な事です。
わたくし
自分で言うのもアレなのかもしれませんが、自分はちょっと数学者でざっくり物理学者でした。動的計画法の改善方法を開発したりしてました。(Iterativeです)
ですので、現在メインで触っているPHPやJavascriptのような表現の伴うプログラミングが苦手です。解が欲しいのです。
C言語をやっていたので、型がないのも未だに気になるし、オブジェクト指向とかもやっとかっとわかるようになったくらいです。着いていけているかは別として。
なので、現在でも共通して使えるであろう技術である、計算量の話にしよう思いました。
計算量
計算量は、コンピュータがアルゴリズムの実行に必要とする計算資源の量のことです。スケーラビリティとかって言うんですかね。
計算量には、時間と空間があります。チューリング機械においては、動作ステップ数やテープの長さで取り扱われていた情報になります。
- 時間計算量
- 作業に必要な計算ステップ数。
- よくランダウの記号(Ο記法)で書かれているのはこちら。
- 空間計算量
- 計算時に必要とするメモリ量。
計算量を測る
完全オリジナルのプログラムであれば計算量を調べることは容易です。入力データのサイズとそれにかかる資源を定式化することで確認できます。
しかし、APIやフレームワークを利用している場合は、その中身まで把握を行わないと計算量がわからない場合があります。
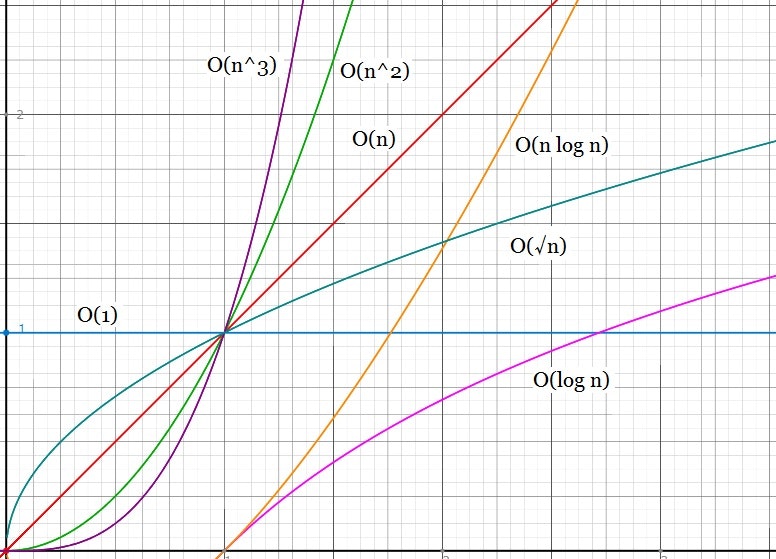
計算量の増加
グラフの横軸がデータ量、縦軸が計算量になります。
どのグラフが節約的でしょうか。
計算量のめやす
データ量が多くなるに連れて、時間的にも空間的にも計算量は黄にしておくべきかと思います。少ないうちは、そうそう変わるものではないらしいです。
(使っていきたいオーダー)
Ο(1) < Ο(log n) < Ο(n) < Ο(n log n)
(ちょっと遠慮したいオーダー)
Ο(n^2) < Ο(n^3)・・・
(雲の上)
Ο(i^n) < Ο(n!)
例
| Ο | 例 |
|---|---|
| Ο(n!) | ボードゲームの先読み。NP完全な問題の全探索・・・?(※1) |
| Ο(i^n) | 要素の組み合わせを調べる場合。巡回セールスマン問題の厳密解の最速手法(※2) |
| Ο(n^3) | 三重ループ。行列計算。 |
| Ο(n^2) | 二重ループ。バブルソートや挿入ソート。 |
| Ο(n log n) | Ο(n)とΟ(log n)をかけ合わせたもの。ヒープソートやクイックソート。 |
| Ο(n) | データの数に比例して時間がかかる。単一のループ処理。 |
| Ο(log n) | 計算が進むに連れ、対象が減少するようなアルゴリズム。既に並んでいる配列を探索する場合など。 |
| Ο(1) | 計算時間がデータ量に依存していない。どんな入力でも必ず同じ時間で処理が終わる。整数の偶数奇数の判定など。 |
ここまで書いてみて
あんまり役に立たない気がしてきました。
ループ数とか、ちょっとした例とかを意識しておくことで、少しでもアルゴリズムの節約(?)ができるといいなぁとか思います。
そういうサンプルプログラムが用意できればよかったのですが、サンプルはネット上にゴロゴロ落ちているため、やりませんでした。(時間があったらやってみます。例えばSQLとかで)
計算量を下げる方法
- データ構造を見直す。
- アルゴリズムを見直す。
知りうる限りではこんな感じです。あまり解説ができません。
例えば、ループ文の中で処理関数を書かないとか、適切なソート手法を使うとかですかね・・・。
終わりに
計算量について知っていることを中心に書いてきましたが、実は罠がありまして、**コンパイルによって最適化される言語もあります。**つまり、意識して書いても書かなくても機械語の時点での計算量が少なくなる場合があります。
また、計算量は入力データが少ない場合は考慮しないです。というか、できないようです。
とは言え、コードレビューや可読性なんかを気にすると、プログラムはシンプルであるべきだと思います。複雑なネストとかをなくすだけでもぜんぜん違うと思います。
精神的・ハード的に負荷の少ないスマートなプログラムが書けるようになりたいです。
以上。
ここまでありがとうございました。
日本情報クリエイト Engineer's Advent Calendar 2017
この後は蛇足です。過去に学習した知識からそれっぽく解説を書いていますが自信がないです。
蛇足なんですけど。
図を作る際に利用したサイトが色々すごくて楽しかったです。すごくきれいにグラフが書けます。
http://graph.tk/
※1 NP完全問題
ぷよぷよとかテトリスです。(論文があります。)
詳しくはWikipediaとか見てほしいです
そもそもNP完全問題の説明をするためにはNPとかPの説明が必要となります。
Pが多項式時間で、NPが非決定性-多項式時間。
非-多項式時間では無いのが覚えるポイント。
NP完全問題はNPの中で最も難しい問題です。
「NPであることが証明」されていて、「他のNPに含まれる全ての問題を多項式時間で変形や操作をすることで同じように帰着できる問題」です。
NPであることが証明されていない場合はNP困難問題となります。
※2 巡回するサンタさん(!)
サンタの国を出発したサンタさんが、世界中のよい子のもとを巡り、サンタの国に帰る。この最短距離を導き出す問題は、NP困難問題となっています。
またの名を巡回セールスマン問題と言います。
動的計画法を用いたアルゴリズムでそれなりに効率的なアルゴリズムがあり現時点での最速手法とされています。(Ο(n!)からΟ(n^2 * 2^n)
youtubeに可視化した動画があったのでおすすめです。
Traveling Salesman Problem Visualization