#FFTの原理および数式
[数式→実装]にフォーカスした記事がなかったので綴ります。
今回紹介するのはCooley–Tukey型FFTのradix-2という最もシンプルなものです。
まず、DFT(離散フーリエ変換)は次の式で表されます。
$$F(t) = \displaystyle \sum_{x=0}^{N-1}f(x) e^{-i \frac{2πtx}{N}} \qquad t=0,1,...,N-1\tag{1}$$
ここで、$N$は入力サイズで、2の累乗に限定します。
$W_N = e^{-i \frac{2π}{N}}$ とし、次のように書き換えます。
$$F(t) = \displaystyle \sum_{x=0}^{N-1}f(x) W_{N}^{tx}\qquad t=0,1,...,N-1\tag{2}$$
入力の偶数番目の要素のみでDFTを行ったものは次の式で表されます。
$$F_{even}(t) = \displaystyle \sum_{k=0}^{\frac{N}{2}-1}f(2k) W_\frac{N} {2}^{tk}\tag{3}$$
同様に、奇数番目の要素のみでDFTを行ったものは次の式で表されます。
$$F_{odd}(t) = \displaystyle \sum_{k=0}^{\frac{N}{2}-1}f(2k+1) W_\frac{N}{2}^{tk}\tag{4}$$
$(3)(4)$を用いることで、$(2)$は次のように書き換えることが出来ます。
$$F(t) = F_{even}(t) +W_N^t F_{odd}(t)\tag{5}$$
ここまでは、普通にDFTを偶奇に分けて変形しただけですね。さて、ここからがFFTの重要なポイントです。実は、$F_{even}(t),F_{odd}(t),W_N^t$は次のような周期性を持ちます。
$$F_{even}(t) = F_{even}(t+\frac{N}{2})\tag{6}$$
$$F_{odd}(t) = F_{odd}(t+\frac{N}{2})\tag{7}$$
$$W_N^t = -W_N^{t+\frac{N}{2}}\tag{8}$$
$(6)(7)(8)$を$(5)$に用いることで、最終的にDFTは次のように書き換えることが出来ます。
$$F(t) = F_{even}(t) +W_N^t F_{odd}(t)\qquad t=0,1,...,\frac{N}{2}-1\tag{9}$$
$$F(t+\frac{N}{2}) = F_{even}(t) - W_N^tF_{odd}(t)\qquad t=0,1,...,\frac{N}{2}-1\tag{10}$$
$F_{even}(t)$と$F_{odd}(t)$は共通なので、これらを求めると同時に$F(t)$と$F(t+\frac{N}{2})$が求まる訳ですね。これが計算量削減の仕組みです。
以上を踏まえて実装に移りましょう。
#FFTのプログラム
FFTの関数をPythonで書いてみます。
基本のアイデアはこうです。入力データを偶数要素と奇数要素に分け、$(3)(4)$のようにFFT(再帰)を行った後、$(9)(10)$を用いて0~(N/2)-1番目とN/2~N-1番目を計算します。よってFFTは再帰関数となります。
def FFT(f):
#f:サイズNの入力データ
N = len(f)
if N == 1: #Nが1のときはそのまま入力データを返す
return f[0]
f_even = f[0:N:2] #fの偶数番目の要素
f_odd = f[1:N:2] #fの奇数番目の要素
F_even = FFT(f_even) #(3)偶数番目の要素でFFT
F_odd = FFT(f_odd) #(4)偶数番目の要素でFFT
W_N = np.exp(-1j * (2 * np.pi * np.arange(0, N // 2)) / N) #tが0~N/2-1番目までのWを計算した配列
F = np.zeros(N, dtype ='complex') #FFTの出力
F[0:N//2] = F_even + W_N * F_odd #(9)を計算(t:0~N/2-1)
F[N//2:N] = F_even - W_N * F_odd #(10)を計算(t:N/2~N-1)
return F
#動作確認
numpyのFFTと同じ出力が得られるか確認してみましょう。
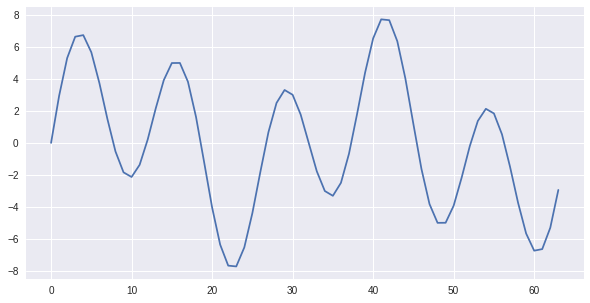
次のようなパラメータで2つのsin波の合成波を作り、これを入力とします。
import numpy as np
import matplotlib.pyplot as plt
N = 64 #データ数
n = np.arange(N)
f1 = 2 #周期1
f2 = 5 #周期2
A1 = 3 #振幅1
A2 = 5 #振幅2
INPUT_f = A1 * np.sin(f1 * 2 * np.pi * (n/N)) + A2 * np.sin(f2 * 2 * np.pi * (n/N)) #2つのsin波の合成
#表示
plt.figure(figsize=(10, 5))
plt.style.use('seaborn')
plt.plot(INPUT_f)
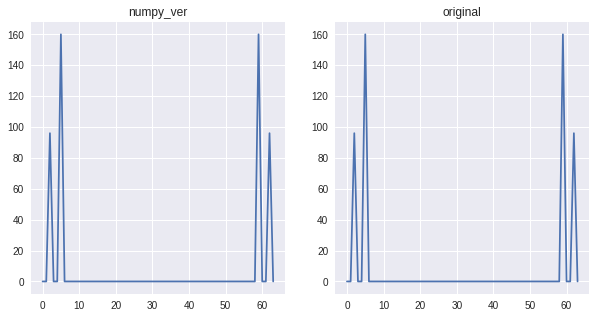
FFTを実行します。FFTの出力は複素数のため、絶対値をかけて振幅成分を取り出し、可視化したものがこちらです。
OUTPUT_F_numpy = np.fft.fft(INPUT_f) #numpy版
OUTPUT_F_original = FFT(INPUT_f) #自作版
plt.figure(figsize=(10, 5))
plt.subplot(1,2,1) #振幅成分表示(numpy版)
plt.title('numpy_ver')
plt.plot(np.abs(OUTPUT_F_numpy))
plt.subplot(1,2,2) #振幅成分表示(自作版)
plt.title('original')
plt.plot(np.abs(OUTPUT_F_original))