はじめに
negocia株式会社では、「うれしい広告」の実現をミッションに、機械学習、数理最適化の技術を活かしたオンライン広告向けのSaaSを開発しています。
今回,Python製凸最適化モデリングツールCVXPYでモデリングする際に求められるDCPルールについて整理してみました.
CVXPYとは?
CVXPYは,Pythonに向けた凸最適化問題のモデリング言語です.CVXPYを使うことで,二次計画問題などの一定の条件を満たす凸計画問題であれば,ソルバーが要求する制限的な標準形式ではなく,数学に沿った自然な方法で問題を表現することができます.たとえば,似たような名前のパッケージであるCVXOPTで二次計画問題を解く際には,二次計画問題の標準形$min \ (1/2) x^\top P x + q^\top x\ s.t\ Gx\le h, Ax=b$に直して,パラメータ$P, q, G, h, A, b$をソルバーの引数として渡す必要があります.ところが,CVXPYでは,DCP(Disciplined Convex Programming)というルールに従ってさえいれば,問題をソルバーの中で解釈し,標準形に直して凸計画ソルバーで解いてくれるという大変便利な機能を持っています.
しかし,私自身実際にCVXPYを利用してみると,どういった条件ならばDCPを満たすのかがよくわからなかったので,今回DCPについて解説している論文を読み,内容をざっくりとまとめました.
DCP(Disciplined convex programming)とは?
Disciplined Convex Programming — CVXPY 1.1.13 documentation
DCPは,最適化を実行する際に,問題への落とし込みを簡単にするためのルールセットです.DCPのルールに沿った定式化であれば,CVXPY上で,自動的に最適化問題を標準形に変換して,凸計画ソルバーで最適化を実行してくれます.
ここで,DCPは,Atom libraryと,凸性のルールセット(Convexity Rule set)の二つの要素から構成されます.
-
Atom library
- 関数や集合(アトム)の拡張可能な集合
- アトムの曲率や形状,単調性やレンジは厳密に明らかにされている
- 凸性のルールセット
- 凸解析の原理から導き出される,アトムや変数パラメータや数値を構成して,凸の結果を生成するためのルール
DCPでは上記二つの構成要素を,定式化された問題に対して判定を行って,DCPに従っているかどうかを判定しています.ここで一つ注意点としては,DCPは凸計画問題となりますが,全ての凸計画問題がDCPになるわけではありません.理由としては,固定したAtomで表現可能な凸計画問題には限りがあるからです.ただし,Atom library自体は拡張可能な形になっているので,自分でカスタマイズすればある程度好きな凸計画問題をモデル化できます.
それではより具体的にこれらの構成要素を分解していきましょう.
まずはAtom Libraryです.利用可能なAtomの集合はこちらから閲覧できます.御覧いただけるとわかるように,Atom Libraryでは,拡張可能な関数と集合のリストに対して,各アトムの曲率や凹凸,単調性や範囲に関する情報が与えられています.DCPでは,このAtomを組み合わせて凸性のルールを守るように問題を構成しなければなりません.
具体的な凸性のルールセットを確認します.Convexity Rule setは,Top level rule, product-free rules, sign rules, composition rulesの四種類のルールがあり,DCPであるためにはこれら全ての条件を満たす必要があります.各ルールの詳細は論文に詳しく書かれているので,参考にしてください.ざっくりと,各ルールの概要を以下にまとめました.
- Convexity Rule setの概要
- Top level rules: 目的関数に関わる条件
- 最小化問題では,凸関数の目的関数,0以上の凸関数の制約条件
- 最大化問題では,凹関数の目的関数,0以上の凹関数の制約条件
- 実行可能判定問題では,目的関数なし,一つ以上の凸制約条件
- などなど...
- product-free rules: 関数同士の掛け算や足し算に関するルール
- 凸関数,凹関数,アフィン表現の合計とスケーリングに関するルール
- 複数の凸関数を足し合わせた関数は凸関数
- 凸関数とnonnegativeな係数の掛け合わせは凸関数
- などなど...
- sign rules: 関数にかかる係数に対してのルール
- あるexpressionが凸関数だとした時,各項c_i * f_i(…)も必ず凸関数である必要がある.
- などなど...
- composition rules: 関数の合成関数に関するルール
- 関数$f$がある限られた領域で凸関数かつ単調増加で,$g$が凸関数の場合には$h=f\circ g$は凸関数になる.
- などなど...
- Top level rules: 目的関数に関わる条件
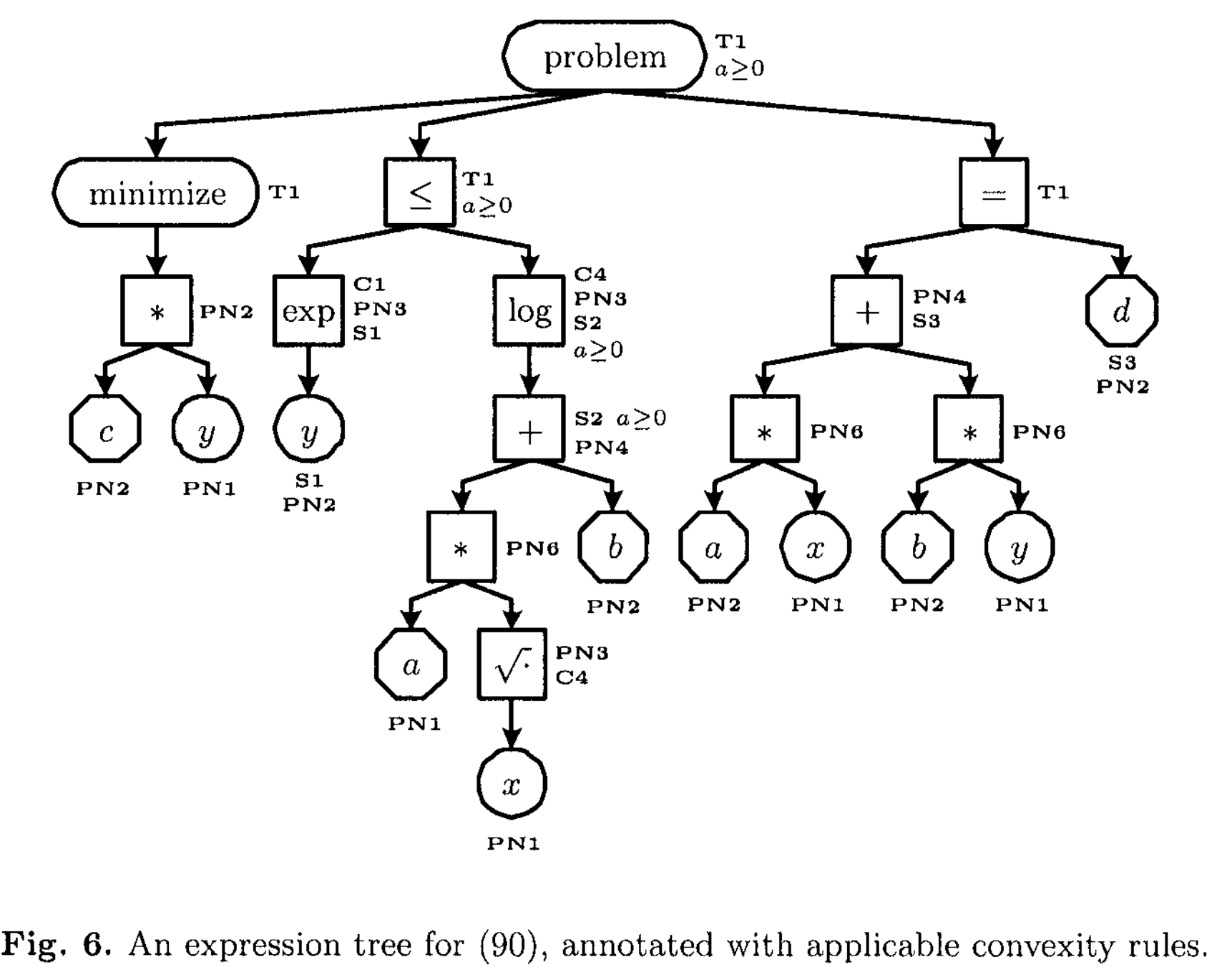
以上が,Atom LibraryとConvexity Rule Setについてまとめた内容になります.なお,プログラム上で定式化された最適化問題がDCPルールに従っているかどうかは,最適化問題をCVXPY内部で計算グラフに分解して判定しています.
DCPとしての定式化
全ての凸計画問題は,DCPに従うとは限らず,たとえ,一般的に凸計画問題として知られている問題だとしても
DCPとして定式化するためには,ソルバーに対してうまくDCPであることを伝える必要があります.たとえば,以下の凸計画問題を考えます.
\begin{equation}
\begin{array}{ll}
\text{maximize}&-\sum_{i=1}^{n} x_{i} \log x_{i} \\
\text { subject to }& Ax=b \\
& 1^{T} x=1 \\
& x \geq 0
\end{array}
\end{equation}
上記問題は,凸計画問題でありますが,DCPのproduct-freeルールを破っているので,以下のように定式化に変更することでproduct-freeルールを守ることができるそうです.
\begin{equation}
\begin{array}{ll}
\text{maximize}& \log \sum_{k=1}^{K_{0}} \exp \left(a_{0 k}^{T} x+b_{0 k}\right) \\
\text { subject to }& \log \sum_{k=1}^{K_{i}} \exp \left(a_{i k}^{T} x+b_{i k}\right) \leq 0 \quad i=1,2, \ldots,m \\
& A^{(m+1)} x+b^{(m+1)}=0\\
\end{array}
\end{equation}
さらに上記定式化だとsignルールを破っているので,Atom libraryを新しく自分で定義する必要があるなど,色々な定式化のテクニックがありますが,詳しくは論文を参照ください.
このようにDCPではなかったら,DCPで解けないわけではなく.規則に従ってきちんと書き直せば,DCPに落とし込むことができるとのことでした.また,既存のAtom Libraryの関数を使って,最適化が実現できない場合でも自前のAtom Functionを定義することによって,ある程度自由に凸計画問題をモデリングできるとのことでした.定式化のテクニックは色々と奥が深そうです.
終わりに
今回は,CVXPYで凸計画問題をモデリングする際に求められるルールセットであるDCPについて調べてみました.CVXPYには他にもルールセット(DPP等)があるので,今後はそれらのルールセットについても整理しようと思います.もしこの記事が少しでも参考になった方がいらっしゃいましたらLGTMボタンで応援よろしくお願いします.