物体検出の評価などで使われる IoU が何かはわかったけれど、具体的な計算方法がよくわからない!
という方がもう迷わないように、NumPy で動作する可読なコードと世界一親切な図付きの解説で最終的解決を図る記事です。
結論
この実装をコピペして使いましょう。b に複数の矩形を入れて a との IoU を一気に計算することにも対応しています。
def calc_ious(a, b):
"""
a: [xmin, ymin, xmax, ymax]
b: [[xmin, ymin, xmax, ymax],
[xmin, ymin, xmax, ymax],
...]
return: array([iou, iou, ...])
"""
import numpy as np
b = np.asarray(b)
a_area = (a[ 2] - a[ 0]) * (a[ 3] - a[ 1])
b_area = (b[:,2] - b[:,0]) * (b[:,3] - b[:,1])
intersection_xmin = np.maximum(a[0], b[:,0])
intersection_ymin = np.maximum(a[1], b[:,1])
intersection_xmax = np.minimum(a[2], b[:,2])
intersection_ymax = np.minimum(a[3], b[:,3])
intersection_w = np.maximum(0, intersection_xmax - intersection_xmin)
intersection_h = np.maximum(0, intersection_ymax - intersection_ymin)
intersection_area = intersection_w * intersection_h
union_area = a_area + b_area - intersection_area
return intersection_area / union_area
使い方
1個の矩形に対して1個の矩形を比較する
# xmin,ymin,xmax,ymax
true_box = [0.2, 0.4, 0.4, 0.7]
pred_box = [0.3, 0.5, 0.5, 0.8]
iou = calc_ious(true_box, [pred_box])[0]
print(iou)
# 0.20000000000000007
多少の丸め誤差が出ていますが、大した問題ではないのでいい感じに処理してください。
1個の矩形に対して複数の矩形を比較する
# xmin,ymin,xmax,ymax
true_box = [0.2, 0.4, 0.4, 0.7]
pred_box_list = [[0.3, 0.5, 0.5, 0.8],
[0.0, 0.1, 1.0, 0.7],
[0.6, 0.8, 0.8, 1.0],]
ious = calc_ious(true_box, pred_box_list)
print(ious)
# [0.2 0.1 0. ]
詳しい仕組み
\textrm{IoU} = \frac{\textrm{Intersection}}{\textrm{Union}} = \frac{共通部分の面積}{合計面積}
を計算するにあたって、「合計面積」は
合計面積 = \textrm{a の面積} + \textrm{b の面積} - 共通部分の面積
で求めることができるため、いかに「共通部分の面積」を計算するかがポイントになります。
a と b それぞれの面積を計算する
念のため矩形の面積の求め方から確認しておきましょう。
右端の x 座標から左端の x 座標を引くと、矩形の幅を求めることができます。
\textrm{width} = x_{\textrm{max}} - x_{\textrm{min}}
図にするとこんな感じです。

同様にして y 座標から高さについても求めたら、矩形の面積を求めることができます。
\textrm{area} = \textrm{width} \times \textrm{height} = (x_{\textrm{max}} - x_{\textrm{min}}) \times (y_{\textrm{max}} - y_{\textrm{min}})
コードが読みやすくなるように、a の左端の x 座標について a[0] と書く代わりに a[xmin] と書いて説明しています。
a_area = (a[xmax] - a[xmin]) * (a[ymax] - a[ymin])
# ┗━━━━━ width ━━━━━┛ ┗━━━━━ height ━━━━┛
b_area = (b[:,xmax] - b[:,xmin]) * (b[:,ymax] - b[:,ymin])
# ┗━━━━━━━ width ━━━━━━━┛ ┗━━━━━━━ height ━━━━━━┛
b は複数ある各矩形について計算され、その結果 b_area はベクトルになります。
すなわち NumPy は b の矩形の数だけ下のような計算をしてくれるということです。
a_area = (a[xmax] - a[xmin]) * (a[ymax] - a[ymin])
b_area[0] = (b[0,xmax] - b[0,xmin]) * (b[0,ymax] - b[0,ymin])
b_area[1] = (b[1,xmax] - b[1,xmin]) * (b[1,ymax] - b[1,ymin])
b_area[2] = (b[2,xmax] - b[2,xmin]) * (b[2,ymax] - b[2,ymin])
共通部分の矩形の面積を求める
共通部分の矩形の幅
共通部分の矩形の幅も、右端の x 座標から左端の x 座標を引くことで求めることができます。
\textrm{intersection_}w = \textrm{intersection_}x_{\textrm{max}} - \textrm{intersection_}x_{\textrm{min}}
共通部分の左端の x 座標とは、 a と b の左端の x 座標のうち大きい方 (max) がこれにあたります。
共通部分の右端の x 座標とは、 a と b の右端の x 座標のうち小さい方 (min) がこれにあたります。
図とコードにするとこんな感じです。
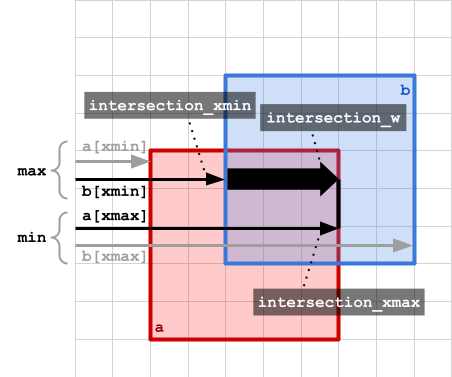

intersection_xmin = np.maximum(a[xmin], b[:,xmin])
intersection_xmax = np.minimum(a[xmax], b[:,xmax])
intersection_w = intersection_xmax - intersection_xmin
次に進む前に、a と b が幅方向に重なっていない場合についても考えてみましょう。
上の式に従うと、intersection_w がマイナスの値として計算されてしまうことがわかります。
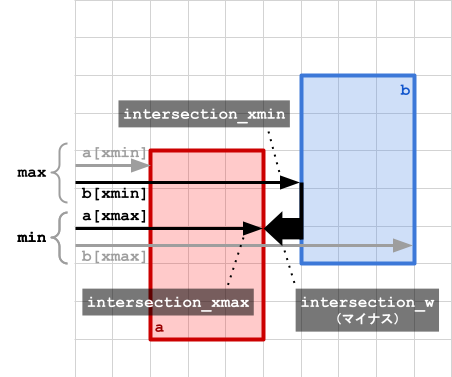
しかしこれは好都合です。intersection_w がマイナスになったということは、a と b が重なっていないと判断できるからです。
共通部分が存在しないわけですから、intersection_w がマイナスのときはゼロに置き換えるようにします。これは 0 と比較して大きい方を取ることで実現できます。
intersection_xmin = np.maximum(a[xmin], b[:,xmin])
intersection_xmax = np.minimum(a[xmax], b[:,xmax])
intersection_w = np.maximum(0, intersection_xmax - intersection_xmin)
なおここで使われている np.maximum() np.minimum() は、b の矩形の数だけ下のような計算をしてくれます。
intersection_xmin[0] = max(a[xmin], b[0,xmin])
intersection_xmin[1] = max(a[xmin], b[1,xmin])
intersection_xmin[2] = max(a[xmin], b[2,xmin])
intersection_xmax[0] = min(a[xmax], b[0,xmax])
intersection_xmax[1] = min(a[xmax], b[1,xmax])
intersection_xmax[2] = min(a[xmax], b[2,xmax])
intersection_w[0] = max(0, intersection_xmax[0] - intersection_xmin[0])
intersection_w[1] = max(0, intersection_xmax[1] - intersection_xmin[1])
intersection_w[2] = max(0, intersection_xmax[2] - intersection_xmin[2])
共通部分の矩形の高さ
y 座標についても同様に計算することで、共通部分の矩形の高さを求めることができます。
\textrm{intersection_}h = \textrm{intersection_}y_{\textrm{max}} - \textrm{intersection_}y_{\textrm{min}}
intersection_ymin = np.maximum(a[ymin], b[:,ymin])
intersection_ymax = np.minimum(a[ymax], b[:,ymax])
intersection_h = np.maximum(0, intersection_ymax - intersection_ymin)
共通部分の矩形の面積
共通部分の矩形の幅と高さが求まったので、ようやく共通部分の面積がわかります。
もし a と b が重なっていない場合は幅もしくは高さのうち少なくとも一方が0になっていますから、積は必ず0になります。安心して掛け算をすることができますね。
intersection_area = intersection_w * intersection_h
IoUを求める
合計面積 = \textrm{a の面積} + \textrm{b の面積} - 共通部分の面積
\textrm{IoU} = \frac{\textrm{Intersection}}{\textrm{Union}} = \frac{共通部分の面積}{合計面積}
union_area = a_area + b_area - intersection_area
iou = intersection_area / union_area
おわりに
IoU 計算の考え方については 物体検出の評価指標IoUの計算方法
IoU と実際の重なり具合のイメージについては IoUの0.1~0.9を図にしてみた
もあわせてご覧ください。
これよりもっといい実装があるぞ等のツッコミもお待ちしております。


