はじめまして。ディープランニングの初学者です。
ニューラルネットワークについて、非常に初歩的ですが理解した内容と簡単な実験結果を纏めてみました。
AIや機械学習の専門家ではないが故の気づきや不明点など色々とあるのではないかと思いますので、同様の立場で学習されている方々の参考になれば幸いです。又、専門家の方からご指導やご指摘を頂けると嬉しいです。
人間の脳は約一千億個の神経細胞(以下ニューロン)により、ニューラルネットワークと呼ばれる巨大な論理回路網を構成しています。(図1)
各ニューロンは情報処理や情報伝達を司り、推論、認知、各種問題解決や学習などの知的活動を行っています。
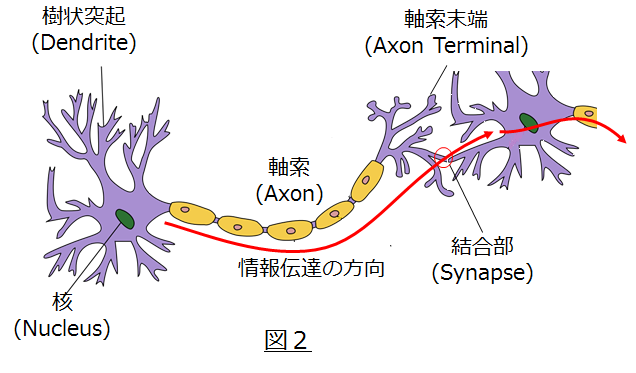
ニューロン単体の構造は図2に示す様に、樹状突起と呼ばれる部分が他のニューロンの軸索末端部とシナプスで結合され、ニューロン間で情報伝達できる仕組みになっています。尚、ニューロン間の信号は電気や化学物質を媒体として伝達されています。
各部の詳細につきましては、Wikipediaが参考になります。https://ja.wikipedia.org/wiki/%E7%A5%9E%E7%B5%8C%E7%B4%B0%E8%83%9E
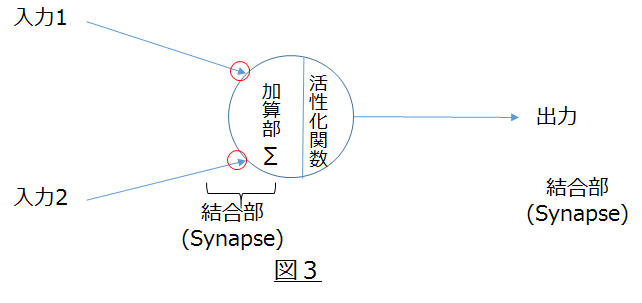
ニューラルネットワークは、図3の様な簡素化した数理モデルに置き換える事ができ、脳が行う推論や学習機能をコンピュータで模倣する事ができます。これが機械学習やディープランニングで実施している事です。
推論(Predict)機能
先ず、単一のニューロンモデルを使いニユーロンが論理積(AND)の計算(推論)が出来る事を見て行きましょう。
ニューロンは特定の事象に関する入力信号を受信すると、過去の学習により獲得したパラメータ値と、活性化関数と呼ばれる出力値を制御する関数に従いある値を出力します。
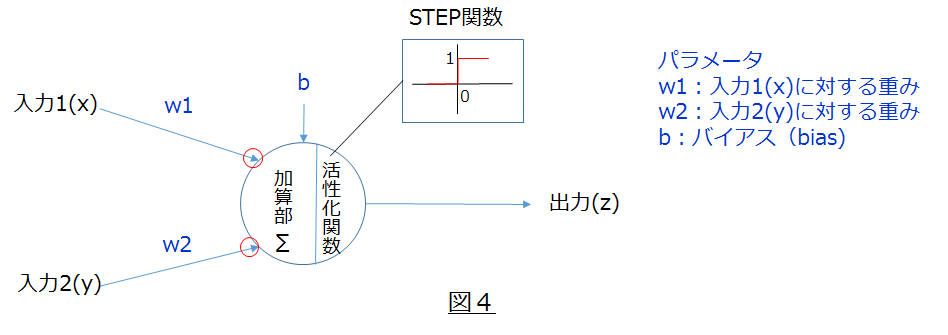
図4に示す様に、パラメータとしては以下の様なパラメータがあります。
w(重み):
受信する信号に対して重みづけをする事で、事象に対応した自身の出力動作を制御する為に下述もb(バイアス)と合わせて受信処理が行われます。
b(バイアス):
ニューロンの発火(出力)のしやすさをを制御します。
これらのパラメータと合わせて、活性化関数と呼ばれる関数を用いて最終的な出力が決まります。
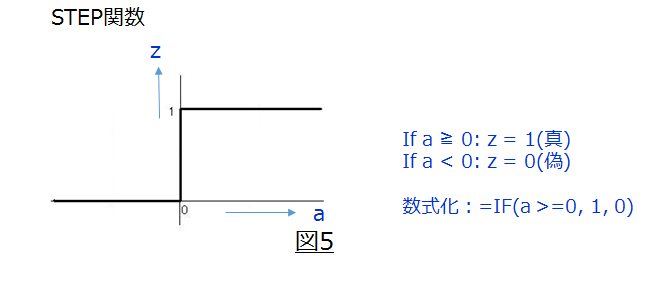
今回は活性化関数として、STEP関数と呼ばれる関数を使用します。(図5)
上記で述べた動きを式で表わすと、以下の様になります。
$a = x * w1 + y * w2 + b$
$z=IF (a >= 0, 1[真], 0[偽])$
数式化できたので、後はPythonやJavaなど得意な言語でコーディングすれば良いのですが、この程度の構成であればExcelを使って計算した方がてっとり早いと思います。
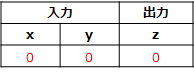
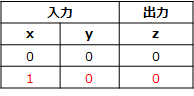
早速、以下の真理値表通りにニューロンモデルが結果を出力(推論)できる事を確認したいと思います。
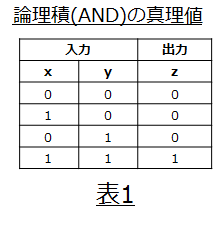
因みに後述の学習が既に済んでいると仮定しますと、論理積(AND)のパラメータは以下の様になります。
w1= 0.5
w2= 0.5
b= -1
$ a = 0 * 0.5 + 0 * 0.5 +(-1) = -1$
$ z = 0 (a < 0)$
$ a = 1 * 0.5 + 0 * 0.5 +(-1) = -0.5$
$ z = 0 (a < 0)$
$ a = 0 * 0.5 + 1 * 0.5 +(-1) = -0.5$
$ z = 0 (a < 0)$
$ a = 1 * 0.5 + 1 * 0.5 +(-1) = 0$
$ z = 1 (a ≧ 0)$
上記の結果は論理演算を使っている訳ではなく、ニューロンモデルが事前の学習結果に基づき正しい出力を推論している事を表しています。
学習機能
無事 推論機能が実装できましたので、ここからはニューロンモデルに学習機能を実装してゆきます。
前述の推論機能の実装では、学習済みのパラメータ(重み[w]とバイアス[b])を利用しましたが、今度は、適切なパラメータ値をニューロn自ら獲得する学習機能を実装します。(パラメータの最適化=学習と思ってください。)
最初に適当な値をパラメータを初期値として与えた後に、ニューロンが試行錯誤を繰り返しながらパラーメータ値を更新し、最終的に適正なパラメータ値を獲得する事をゴールに以下のプロセスを実行します。
1.パラメータを初期化
2.推論を実施
3.正解との誤差を算出
4.パラメータを学習アルゴリズムにより更新
5.更新後のパラメータで推論を実施
6.正解を得られるパラメータ値が獲得できる迄、2~5を繰り返す。
1.パラメータの初期化
w1= 1
w2= -1
b= 0
2.推論を実施
$ a = 0 * 1 + 0 * (-1) + 0 = 0$
$ z = 1 (a ≧ 0)$
正解はz=0なので推論結果は間違い。
3.正解との誤差を算出
0[正解]-1[誤] = -1[誤差]
4.パラメータを学習アルゴリズムにより更新
学習率を = 0.5に設定(人の設定するハイパーパラメータでパラメータの更新度合を調整)
更新後 w1 = 0[入力1] * (-1)[誤差] * 0.5[学習率] + 1[更新前 w1] = 1
更新後 w2 = 0[入力1] * (-1)[誤差] * 0.5[学習率] + (-1)[更新前 w2] = -1
更新後 b = -(0[更新前 b]-((-1)[誤差]* 0.5[学習率]) = -0.5
上記のアルゴリズムですが、正直なところ何故これで上手く行くのかがまだ理解できていません。
通常損失関数をパラメーターで偏微分して得られる勾配を使い、パラメーターを勾配の下降方向に更新すると思うのですが、自分の頭の中で其の辺りがしっくり行っていない状況です。
取り敢えず、活性化関数に微分のできないSTEP関数を利用している為と言うことで進めて行きます。
5.更新後のパラメータで推論を実施
$ a = 1 * 1 + 0 * (-1) +(-0.5) = 0.5$
$ z = 1 (a ≧ 0)$
正解はz=0なので推論結果は間違い。
6.正解を得られるパラメータ値が獲得できる迄、2~5を繰り返す。
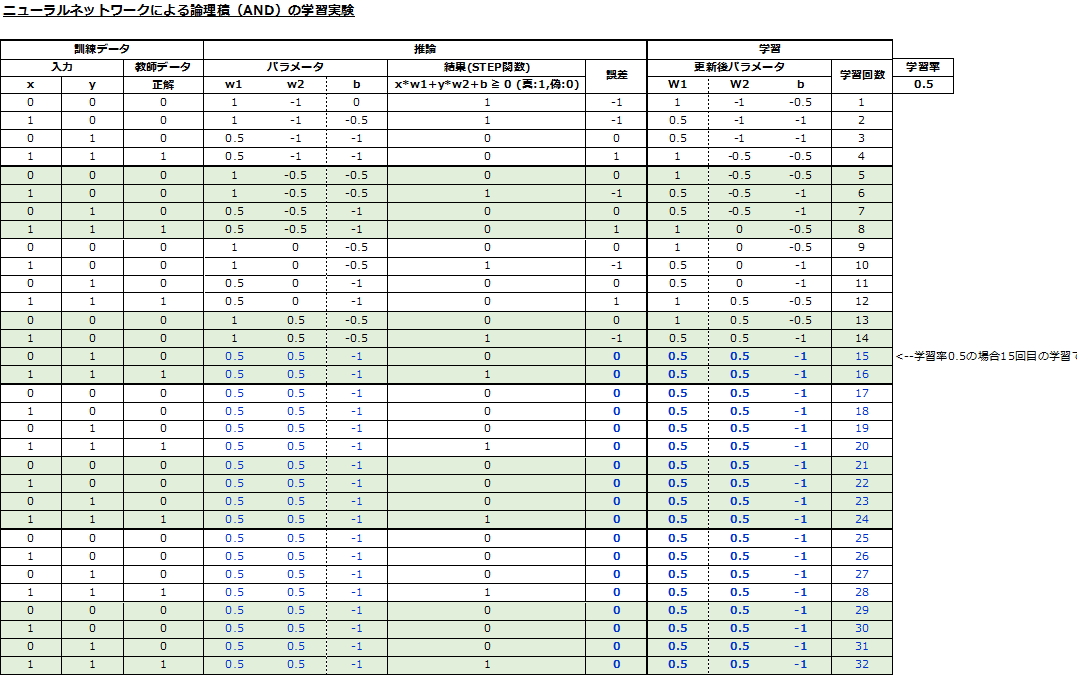
以下に、エクセルに上述の推論と学習のアルゴリズムの式を記載し機械学習を実行した結果を示します。
これによると、15回目の学習で、全入力に対して正解を出力できるパラメータ値が獲得された事が確認できます。
w1= 0.5
w2= 0.5
b= -1
他の論理演算での確認
今回は論理積(AND)に対する学習を実施しましたが、次に他の論理演算に対しても同様の機械学習実験を行ってみます。
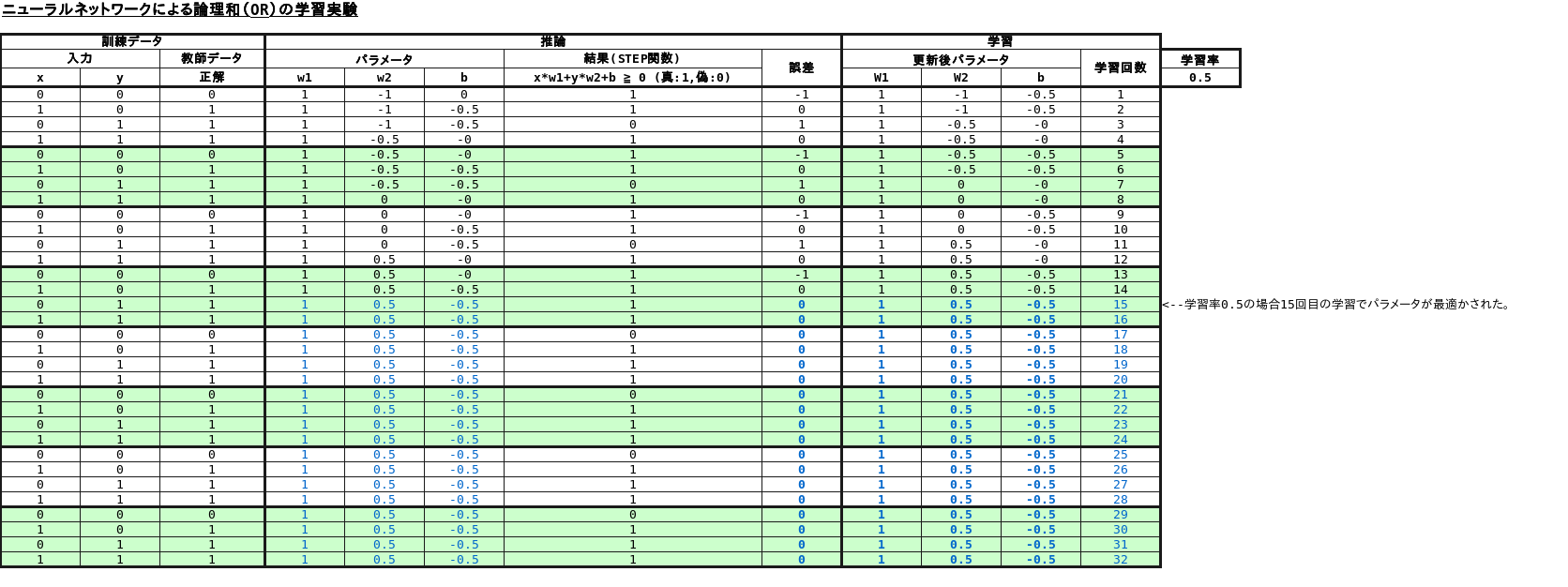
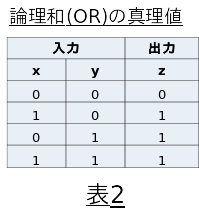
論理和(OR)
論理和(OR)も15回目の学習でパラメータが以下の通り最適化されました。
w1= 1
w2= 0.5
b= -0.5
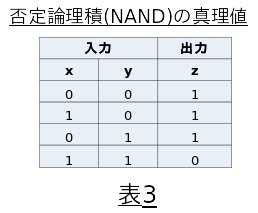
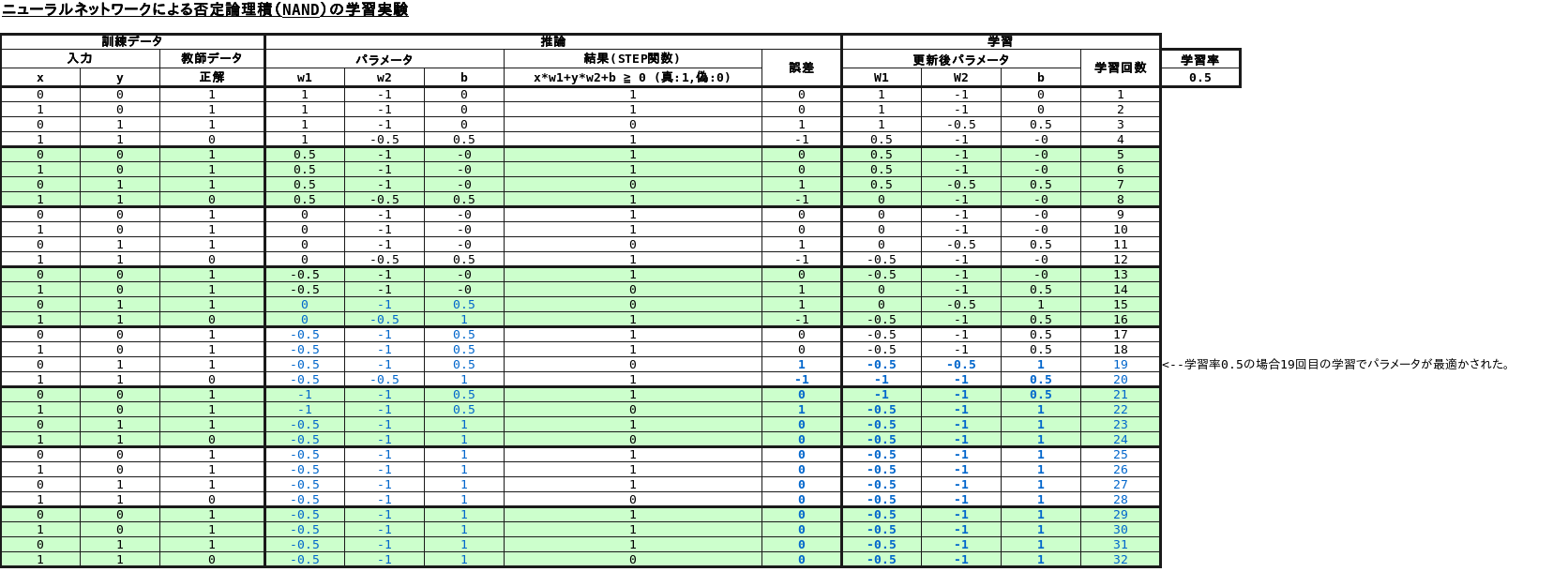
否定論理積(NAND)
否定論理積(NAND)は19回目の学習でパラメータが以下の通り最適化されました。
w1= -0.5
w2= -1
b= 1
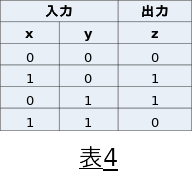
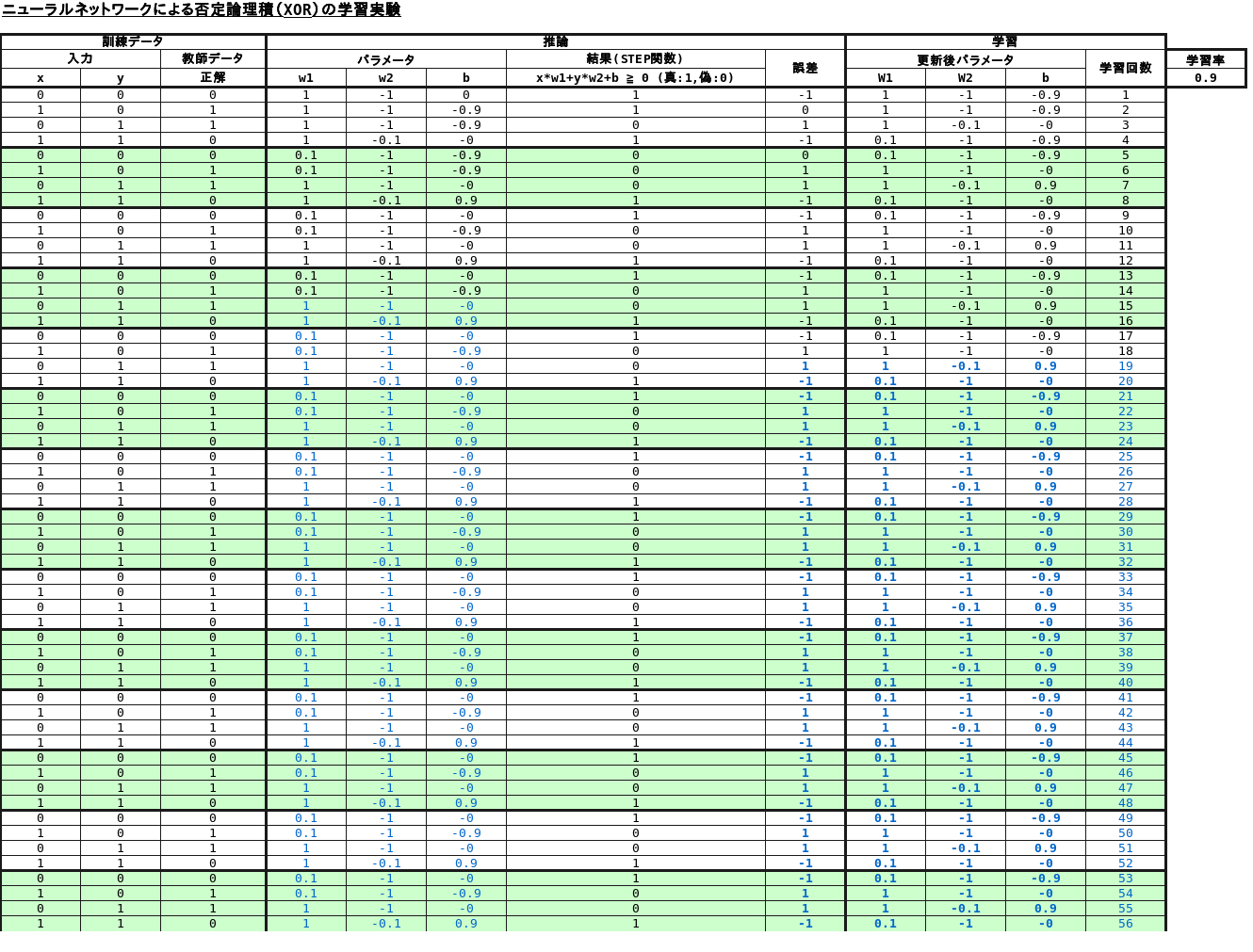
排他的論理和(XOR)
排他的論理和(XOR)については、学習が収束しない事が分かりました。
他の文献にも記載されている様に、NAND回路を多段化する事で可能になる様です。
まとめ
シンプルなニューラルネットワークをエクセルで実装し、学習を通じて、正しく論理計算の真理値表通りの結果を出力できる様になる事を確認できました。
非常に簡単な実験ですが、ニューラルネットワークが学習する様子を実感する事ができ感動しました。
今後は本来的的なディープランニングの実装に挑戦してみたいと思います。