実は結構複雑な、分類問題の評価についてまとめます。
シンプルな二値分類から、多値分類、他ラベル分類までまとめます。
2値分類タスク(binary classification)
入力に対して、Positive or Negativeのどちらかを返す二値分類タスクのモデル評価について考えます。この場合、評価データセットの各exampleに対して、正解ラベルとモデルが予測したラベル(予測ラベル)が与えられています。
事前知識:TP、TN、FP、FN
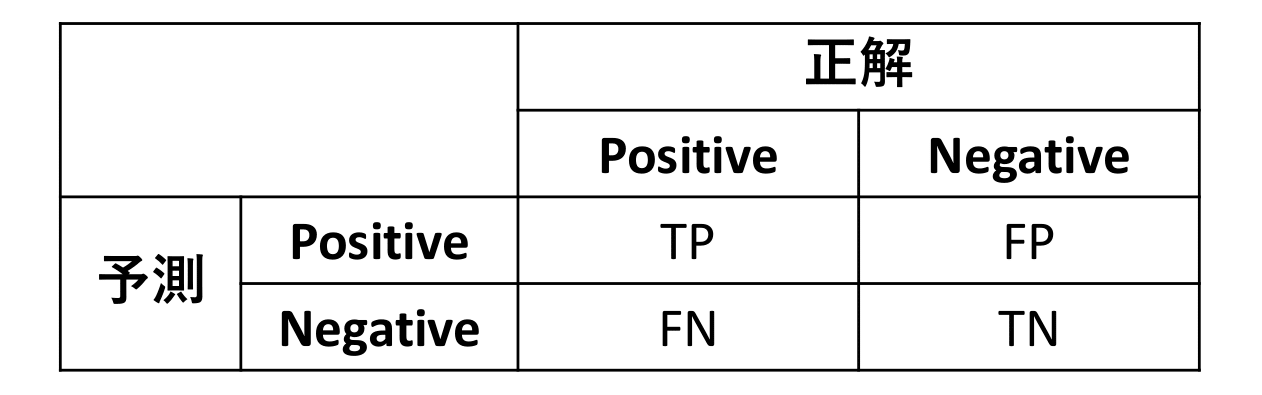
二値分類において、各exampleに対する予測結果は以下のどれかです。
- True Positive (TP):モデルがPositiveと予測して、正解がPositive
- True Negative (TN):モデルがNegativeと予測して、正解がNegative
- False Positive (FP):モデルがPositiveと予測したが、正解がNegative
- False Negative (FN):モデルがNegativeと予測したが、正解がPositive
これらを使って各評価手法の説明をしていきます。
Acuracy
2値分類タスクの評価として最もかんたんな評価方法はAccuracyでしょう。この評価方法では、モデルが正解ラベルを予測した割合で評価します。
数式で表せば、
$$
\textrm{accuracy} = \frac{\textrm{TP} + \textrm{TN}}{\textrm{TP}+\textrm{TN}+\textrm{FP}+\textrm{FN}} = \frac{\textrm{TP}+\textrm{TN}}{N}
$$
となります。
Accuracyの問題点
評価データセットに含まれるPositiveとNegativeの数に大きな偏りがある場合や、PositiveとNegativeの重要度が変わる場合に、accuracy評価ではその実態が正しく表現されない場合があります。例として、全人口の2%が罹る病を判定するタスクを考えてみましょう(病に罹っている場合にPositiveです)。
このタスクに対して、必ずNegativeと返すモデルをがあったとすると、評価データの98%はNegativeなのでモデルのaccuracyは98%となります。しかし、実際には病に罹っている人は一人も見つけられません。このようなモデルは全然使えないでしょう。このような場合において、正しくモデルの性能を測るためにRecallやPrecisionがあります。
Recall
Recallは正解がPositiveなexampleのうち、正しくPositiveと判定できた割合です。
数式で書くと
$$
\textrm{recall} = \frac{\textrm{TP}}{\textrm{TP}+\textrm{FN}}
$$
となります。
先程の例で、全人口の2%が罹る病を判定するタスクに対して、全てNegativeと答えた場合は、TP=0となるのでrecallは0です。つまり、recallは網羅率を図っていると考えることができます。
Recallによる評価では、逆にすべての患者に対してPositiveと予測した場合、FNがなくなるのでrecall=1となります。この問題を解決するために、precisionがあります。
Precision
PrecisionはモデルがPositiveと判定したexampleのうち、実際に正解ラベルがPositiveである割合です。
数式で書くと
$$
\textrm{precision}=\frac{\textrm{TP}}{\textrm{TP}+\textrm{FP}}
$$
となります。
同様に、全人口の2%が罹る病を例にします。あなたが、ある分類器によってPositiveであると判定されたとします。このとき本当にPositiveである確率を示すのがprecisionです。
Precisionが低い場合、Negativeな人(健康な人)に誤ってPositiveである(病気である)と診断してしまい、不要な心配をかける確率が上がります。
F値
Recallとprecisionはトレードオフの関係にあります。モデルが積極的にpositiveと答える場合、positiveであるexampleをnegativeであると判定する確率は下がるためrecallは上がりますが、逆にpositiveと判定したもののうち実際にはnegativeである割合が多くなりprecisionは低下します。
F値はその折半案になります。
数式で書くと
$$
\textrm{F}=\frac{2\cdot\textrm{recall}\cdot\textrm{precision}}{\textrm{recall}+\textrm{precision}}
$$
となります。
いつ、どの評価を使うか
様々な評価方法がある中で、どの状況でどの方法を使うかを考えます。
ここで、考えないと行けないのは
- 測りたい性質(分類の目的)
- データの分布
の二点です。
スパムメールを判定する分類器を評価するとします(Positive=スパム)。このとき、スパムではないメールがスパムとして判定されてしまい、ユーザーの目に入らないと大きな問題になります。逆にスパムメールがスパムでは無いと判定されメールボックスに入ってしまってもそこまで(相対的に)大きな問題ではありません。このような場合はprecisionが有用な評価方法となるでしょう。
逆に、病気の判定では、病に罹っている人(Positive)を誤って健康である(Negative)と判定すると重大な問題になります。その場合は、recallが十分高いことを確認する必要があります。
このようにFalse PositiveとFalse Negativeの重要度(costとも言う)に大きな差がある場合は、recallやprecisionが良い評価方法となります。
それぞれの重要度があまり変わらない場合は、accuracyかF値かを選択することになります。この場合はデータの分布に着目をする必要があります。前に述べたように、データの分布が大きく偏っている場合、accuracyは分類器の性能を正しく表現できないことが多いです。その場合はF値でないと正確な評価はできませんが、データが十分バランスされている場合は明確でわかりやすいaccuracyが良い評価手法となりそうです。
実際の運用では、とりあえずすべての評価値を出力してみることをおすすめします。これらの値を眺めることで、モデルの性質やデータセットの性質がわかることがよくあるからです。
多クラス分類タスク(multi-class classification)
次に2つ以上のクラスの中から一つを選択する他クラス分類タスクの評価について考えます。この場合は、クラスを一つ選びPositiveとしそれ以外をNegativeとして評価値を計算したあとそれらの平均を取ることで全体の評価値を計算します。このときの平均のとり方としてmicro平均とmacro平均があります。
macro平均
3つのクラス(A、B、C)の分類タスクを考えます。このとき、AをPositiveとしてB、CをともにNegativeとした際の$\textrm{TP}$、$\textrm{TN}$、$\textrm{FP}$、$\textrm{FN}$をそれぞれ、$\textrm{TP}_A$ 、$\textrm{TN}_A$、$\textrm{FP}_A$、$\textrm{FN}_A$とします。
これらを使って、クラスAのaccuracy、precision、recall、F値が計算できます。
\begin{align}
\textrm{accuracy}_A &= \frac{\textrm{TP}_A + \textrm{TN}_A}{\textrm{TP}_A+\textrm{TN}_A+\textrm{FP}_A+\textrm{FN}_A}\\
\textrm{recall}_A &= \frac{\textrm{TP}_A}{\textrm{TP}_A+\textrm{FN}_A}\\
\textrm{precision}_A &= \frac{\textrm{TP}_A}{\textrm{TP}_A+\textrm{FP}_A}\\
\textrm{F}_A &= \frac{2\cdot\textrm{recall}_A\cdot\textrm{precision}_A}{\textrm{recall}_A+\textrm{precision}_A}
\end{align}
これらの値は、各クラス毎に計算できます。これらの平均をとるのがmacro平均です。
\textrm{accuracy}_M = \frac{\textrm{accuracy}_A+\textrm{accuracy}_B+\textrm{accuracy}_C}{3}
(その他の評価値も同様)
micro平均
各クラスのexample数が大きく異る場合に、macro平均はでは実際の精度が計算できない場合があります。
クラスA、B、Cのデータ数が100、10、10であり、それぞれのクラスのaccuracyが0.1、0.9、0.9であるとします(各クラスの正解数は10、9、9)。このとき、macro-accuracyは $\frac{0.1+0.9+0.9}{3}=0.63$ となりますが、実際に正しく正解を当てられる割合は $\frac{10+9+9}{120}=0.23$ です。
ここで計算した、$0.23$がmicro-accuracyになります。つまり、クラスごとではなく各exampleごとのaccuracyの平均です。
micro平均はaccuracyに限らず、precision、recall、F値に対しても計算できますが、全てaccuracyと同じ値になります。
多ラベル分類タスク(multi-label classification)
多クラス分類問題では複数のクラスから一つの正解を選ぶタスクでしたが、多ラベルタスクでは正解が複数あるようなタスクです。例えば、qiitaの記事からそのタグを予測するようなタスクが多ラベル分類タスクになります。(多クラス問題も多ラベル問題のうち正解ラベルが1つである場合と考えられます)
この場合、正解もモデルの出力も集合となります。そこで、$i$番目のexampleの正解を$T_i$, モデルの予測を$Y_i$として評価手法を考えていきます。
最もシンプルな評価指標は、exact match ratioです。これは、モデルがすべてのラベルをもれなく正確に予測した割合です。
\textrm{ExactMatchRatio}=\frac{1}{N}\sum_{i=1}^{N}I[Y_i=T_i]
($N$が評価セットの大きさ、$I[\cdots]$は$\cdots$が正しいときに1、そうでないときに0)
この評価手法では、一つだけ漏れがあった場合も、全く異なる予測をした場合も同じように「間違い」になってしまいます。
そこで、部分的な正解を考慮したaccuracy, precision, recallが提案されています。
\begin{align}
\textrm{accuracy}&=\frac{1}{N}\sum_{i=1}^{N}\frac{|Y_i\cap T_i|}{|Y_i\cup T_i|}\\
\textrm{recall}&=\frac{1}{N}\sum_{i=1}^{N}\frac{|Y_i\cap T_i|}{|T_i|}\\
\textrm{precision}&=\frac{1}{N}\sum_{i=1}^{N}\frac{|Y_i\cap T_i|}{|Y_i|}
\end{align}
よく見ると、precisionは予測したラベルのうち正解であった割合、recallは正解のラベルのうち正しく予測した割合を計算していることがわかります。
極端な例を見てみましょう。例えば、モデルが常に空集合を予測結果として出すとします($Y_i=\emptyset$)。この場合、precisionはゼロ割が発生して計算できません(感覚としては1になります)。recallは逆に0となります。逆に、モデルが全ラベルを正解として出す場合は、$Y_i=\Omega$なので、precisionは小さくなり($|T_i|/|\Omega|$)、recallは1になります。
つまり、モデルが大きな集合を予測すればするほど、recallは上がりprecisionが下がるのです。
ランキングベースのモデルの評価
多ラベル問題では、各クラスに対するスコアを計算するモデルを活用することがあります。たとえば、膨大な文書集合から関連する文書を出力する検索タスクや、商品全体からおすすめの商品を提案するレコメンドタスクでは、入力(クエリやこれまでの購入履歴)をもとに各文書や商品に対してスコアを計算し、スコアの高い結果を出力します。
ここで、各文書や商品をラベルと考えれば、モデルの出力はラベルのランキング(スコア付き)と考えられます。このようなモデルの評価を考えます。
最もシンプルには、ランキングのtopkをモデルの予測した集合($Y_i$)として多ラベル問題の評価手法を用いる方法が考えられます。この場合の評価手法はtopk-precisionやprecision@kなどと呼ばれます。
更に、ランキング特有の評価手法にcoverageがあります。
Coverageはランキングを上から見ていき、どこまで見れば正解ラベルをすべてカバーできるかを計算します。この手法では値が小さければ小さいほど、良いモデルということになります。
\textrm{coverage}=\frac{1}{N}\sum_{i=1}^N\max_{t\in T_i} r_i(t)-1
($r_i(t)$はラベル$t$のランク)
つまり、正解ラベルのうち一つでもランキングで下位になってしまう場合、covarageによる評価は大きく低下します。
正解ラベルをすべて見つけないといけないような場合(ハッキング検知など)で有用な評価手法になります。
まとめ
分類タスクの基本的な評価手法についてまとめました。機械学習において評価手法はあまり着目されないことが多く、「とりあえずscipyとかでaccuracy出しとけばいいっしょ」となっている人も多そうですが、適切に使わないと測りたいことを正確に測れないことが多々あります。また、一つの評価手法がモデルの性格な性質を表すことはほとんど無く、それぞれの性質を理解しつつ複数の評価手法を併用し、実際の予測例もしっかりと確認していくことが必要です(自戒)。