固定小数点数と浮動小数点数について
固定小数点数
・固定終点は、「ビット列のどの位置に小数点があるか」を暗黙的了解として扱う表現方法
・少数を固定する位置は、ソフト実装によってきまります。
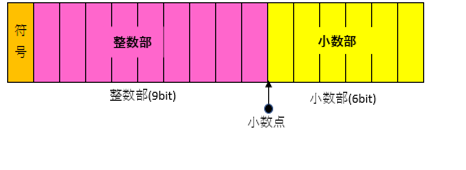
または、このように表現することも可能です。
浮動小数点数
・固定小数点数で制限されていた表現できる数値の範囲広げるための方法です。
例を挙げると以下の通りになります。
10進数:0.00025の場合
「2.5(仮数部)× 10-4(指数部)」
仮数部と指数部を変えることで、様々な表現ができます。この時により有効桁を多くとれるように、
小数点の位置を調整し仮数部の最上位桁を0以外の数値にすることを正規化といいます。
また、記号で表現すると以下の通りになります。

論理回路と基本回路
・論理演算する回路が論理回路という、基本的には以下の3種類 ※以下の回路は基本回路とも呼ばれております。
・論理積回路(AND)
・論理和回路(OR)
・否定回路(NOT)
論理積回路(AND回路)
・入力がどちらも「1」だった時に、「1」を出力するのが論理積回路(AND回路)になります。

論理演算は論理式という式であらわすことができます。
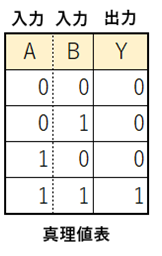
この時、入力としてA、Bが取り得る値の組み合わせは全部で4パターン。これに対応する出力Yをくっつけて表としてまとめたものが真理値表と言います。
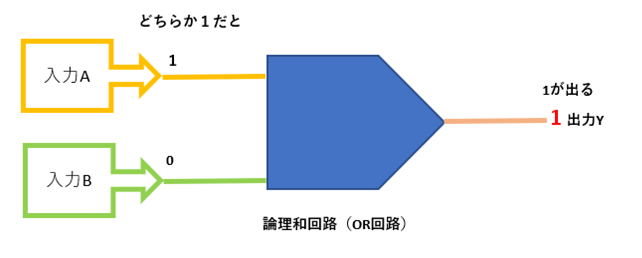
論理和回路(OR回路)
・入力がどちらが1つでも「1」だった時に、「1」を出力するのが論理和回路(OR回路)になります。
論理和(OR)を示す演算記号は「+」。したがって、この場合の論理式は次のようになります。
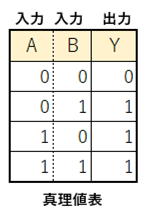
論理和回路(OR回路)の真理値表は以下の通りになります。
否定回路(NOT回路)
・入力が「0」なら「1」、「1」なら「0」を出力するといった具合に、入力値を反転させて出力するのが否定論理(NOT回路)になります。
否定(NOT)を指揮であらわすときは、値の上に「-」を付加して表現します。
入力としてAとり得る値は2パターン
否定回路(NOT回路)の真理値表は以下の通りになります。