【完全版】NumPyの使い方を徹底解説【機械学習】

NumPy（ナムパイ）とは、高速計算処理を得意とするPythonのライブラリです。


機械学習をPythonで行う場合は、NumPyをよく使います。

本記事では、NumPyの基礎的な文法を徹底解説します。

ベクトルや行列の概念の説明から、基礎文法の図解まで、Python初心者でも挫折せずに学ぶことができます。

是非ブックマークして、何度も見返すことをオススメします。

この記事を執筆した筆者について

データサイエンス関連を学習中の若手SEです。

機械学習、データ分析といったデータサイエンスに関する記事を投稿中ですので、こちらも合わせて御覧ください。

■ブログ：https://datascience-lab.sakura.ne.jp
■Youtube：https://www.youtube.com/channel/UCwlSTr8FIuNnaNPZIzDghAA
■Twitter：https://twitter.com/juri_engineer

なぜ機械学習でNuｍPyを使うの？

NumPyを使う理由は、大量のデータを計算するのに適しているからです。

機械学習はデータ量が多いほど精度が上がりやすいので、データを処理する速度は非常に大切なポイントです。

NumPyは機械学習に適したライブラリなのです。

なぜ計算が早いのか

NumPyはベクトル演算を使うことで、ループをせずに配列や行列の計算ができます。

ベクトルや行列、配列は、後ほど解説します。

次元とは

NumPyの文法に入る前に、基本的な概念・用語について確認しておきましょう。

NumPyでは「次元」という言葉がよくでてきます。

次元とは、空間の広がりを表します。

・一次元というのは、軸が1本、つまり、点と直線のみで表現されます。
・二次元は、軸が2本なので、面を表します。
・三次元は、軸が3本なので、立体を表します。

ベクトルと行列

ベクトルとは

NumPyでいうベクトルとは、数字や文字列が複数連なったものです。

ベクトルは、配列の一種です。
列が1列なので、1次元配列です。

ベクトルの長さは、要素数です。

上記の例にあるベクトルAは、要素数が5なので、長さ=5です。

行列とは

行列とは、行と列からできた数字や文字列の集まりです。

行と列からなる行列は、二次元配列とも呼ばれます。

それぞれのデータを、要素と呼びます。

行列は、大文字のアルファベットを使って表現します。


上記の例では、行列Aと名付けられています。

行と列の覚え方は、下記がおすすめです。

漢字で考えるとわかりやすいです。

行列はどんなサイズも取ることができ、一般的にm×nの行列Aと表現します。

一方で、特定の要素は小文字で表現されます。（例：a₂₂）

例えば、aijは、i行j列にある要素を表現できます。

スカラー

1,2,3...のように、数字単体を表します。次元がありません。

0次元です！

配列とは（ndarray配列）

配列とは、複数の要素を入れておくための入れ物のイメージです。

NumPyで提供される配列は、ndarrayと呼ばれます。

配列は複数のデータ型の要素を格納できるのに対し、ndarray配列は一種類のデータ型しか格納できません。

ベクトルは一次元、行列は二次元ですが、ベクトルも行列もndarray配列の一種です。

リスト・タプル・ディクショナリとベクトルの違い

pythonで使う代表的なデータ型として、リストやタプル、ディクショナリ（辞書型）があるけど、ベクトルとどういった点が違うのでしょう？

ベクトルと、リスト・タプル・ディクショナリとの違いは、数字・文字列などの複数のデータ型を1つのリストに格納できるかどうかです。

• ベクトル：要素のデータ型は1種類のみ
• リスト・タプル・ディクショナリ：複数のデータ型の要素を入れられる

リスト

リストとは、要素を並べたものです。

list = [5,10,15,20]
list

>> 実行結果
[5, 10, 15, 20]

ベクトルとの違いは、数字・文字列などの複数のデータ型を1つのリストに格納できるかどうかです。

#リストは複数のデータ型を格納できる
list2 = [1,"apple",4.5]
list2



>>実行結果
[1, "apple", 4.5]

タプル

タプルも、リストと同様に要素を並べたものです。

定義する時に、リストは角括弧で囲むのに対し、タプルは丸括弧で囲みます。

#タプルの定義
tuple = (1,2,3)
tuple

>>実行結果
(1, 2, 3)

リストと異なり、タプルは一度定義すると、上書きや追加をすることができません。

#タプルは上書きできない
tuple[1] = 10

>>実行結果
TypeError: "tuple" object does not support item assignment

ベクトルとタプルの違いは、リストと同様、複数のデータ型を入れられるかどうかです。

ディクショナリ

ディクショナリ（辞書型）とは、keyとvalueをセットで格納できるデータ型です。

#辞書型を定義
dict = {"No.1":"apple", "No.2":"orange", "No.3":"banana"}
dict


>>実行結果
{"No.1": "apple", "No.2": "orange", "No.3": "banana"}

リストと同様に、複数の異なるデータ型を格納することができます。

NumPyの基本的な使い方

※編集途中（コード部分）。完成版は、下記リンクをご参照ください※
https://datascience-lab.sakura.ne.jp/numpy/

インポート

まずは、NumPyをインポートすることで、手元のPythonファイルでNumPyを使えるようにしましょう。

一般的に、NumPyはnpとしてインポートします。

#NumPyをimport
import numpy as np

ndarray配列の作り方

ベクトルの作り方

ndarray配列を作る時は、NumPyに含まれる関数arrayを使います。

事前に作ったリストをndarray配列に変換するイメージです。

ここでは、ベクトルを作成します。

#リストの作成（一次元）
data = [1,2,3,4]
#array関数でndarray配列にする
a = np.array(data)
a
>>実行結果
array([1, 2, 3, 4])

行列（マトリックス）の作り方

行列もndarray配列の一種です。


そのため、ベクトルを生成した時と同様、array関数を使います。

#1リストが1行になる
data2 = ([1,2,3,4],
         [5,6,7,8],
         [9,10,11,12])
#array関数で行列にする
b = np.array(data2)
b
>>実行結果
array([[ 1,  2,  3,  4],
[ 5,  6,  7,  8],
[ 9, 10, 11, 12]])

初期化配列を作る【zeros関数】

全ての要素が0のベクトルや行列を作りたい場合は、zeros関数を使います。

0で初期化されているベクトルや行列がほしい時に使います。

#１次元配列（ベクトル）
zeros = np.zeros(10) 
zeros
>>実行結果
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

#2次元配列はタプルで行数・列数をそれぞれ指定する
zeros2 = np.zeros((4,5))
zeros2
>>実行結果
array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])

全ての要素が1の配列を作る【ones関数】

全ての要素が1のベクトルや行列を作るときは、onesを使いましょう。

#全ての要素が1のベクトルを作る
np.ones(4)
>>実行結果
array([1., 1., 1., 1.])

#全ての要素が1の行列を作る
np.ones((3,5))
>>実行結果
array([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])

全ての要素を指定した数でベクトルや行列を作る【full関数】

np.full(5,3)
>>実行結果
array([3, 3, 3, 3, 3])

対角線上の要素を1にした行列を作る【eye関数】

行列の対角線上の要素を1、他の要素を0にした行列を作る時は、eye関数を使います。

np.eye(4)
>>実行結果
array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])

等間隔の行列を作る【arange関数】

等間隔の要素が格納されたベクトルを作る時は、arange関数を使います。

#arange(終わりの数字)
np.arange(5)
>>実行結果
array([0, 1, 2, 3, 4])

#arange(始める数字, 終わりの数字)
np.arange(5,10)
>>実行結果
array([5, 6, 7, 8, 9])

#arange(始める数字, 終わりの数字, 間の数字)
np.arange(5,50,3)
>>実行結果
array([ 5,  8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, 47])

ベクトルを行列にしたい場合は、reshape関数を使います。

#行列にする
np.arange(5,50,3).reshape(5,3)
>>実行結果
array([[ 5,  8, 11],
[14, 17, 20],
[23, 26, 29],
[32, 35, 38],
[41, 44, 47]])

中身を調べる

配列の形状を調べる

各次元ごとの要素数を表示したい場合は、属性shapeをつかいます。

ndarray配列名.shapeで、ベクトルや行列のサイズを表示してくれます。

#ndarray配列の形状を調べる
a.shape
>>実行結果
(4,)

aは一次元配列です。

一次元配列は軸が列のみなので、4は要素数を表すことになりますね。

4×1の行列とも言えます。

shapeは、引数にndarray配列名を指定する方法でも使えます。

np.shape(a)

行列の形状も調べることができます。



下記の例では、3×4の行列であることがわかりました。

#行列の形状もわかる
b.shape
>>実行結果
(3, 4)

次元を確認する

ndarray配列が何次元なのかを確認したい場合は、属性ndimを使います。


ndarray配列aは一次元なので、実行結果は1となります。

#次元を確認する
a.ndim
>>実行結果
1

行列bは二次元のため、実行結果は2になりました。

#行列は2次元
b.ndim
>>実行
2

引数にndarray配列を指定する方法でも、同様の結果が得られます。

#引数に指定する方法でも使える
np.ndim(a)

データ型を確認する

ndarray配列名.dtypeで、ndarray配列に格納されている要素のデータ型を確認できます。

#データ型の確認
a.dtype
>>実行結果
dtype('int64')

行列でも、同様にデータ型が確認できます。

b.dtype
>>実行結果
dtype('int64')

intの後に64という数字が入っていますが、これはビット数を表します。

ビット数とは、データのサイズで、数字が大きいほどデータも大きいことを表します。

ビット数が大きいと、計算の処理速度が遅くなります。




要素が文字列なら、unicode型になります。

data = ["apple", "banana", "orange"]
c = np.array(data)
c.dtype
>>実行結果
dtype('<U6')

要素が小数なら、float型になります。

#要素が小数なら、float型
data = [0.1,0.04,6.9]
d = np.array(data)

要素数を調べる

全ての要素数を確認するときは、属性sizeを使います。

#要素数の確認
a.size
>>実行結果
4

行列のときも同様に確認できます。

b.size
>>実行結果
12

統計量

平均

平均は、mean関数を使うことで簡単に算出できます。

np.mean(a)
>>実行結果
2.5

引数でaxis属性を指定することで、行ごと・列ごとの算出も可能です。

#行列の行ごとの平均を知りたい場合
np.mean(b,axis=1)
>>実行結果
array([ 2.5,  6.5, 10.5])

#行列の列ごとの平均を知りたい場合
np.mean(b, axis=0)
>>実行結果
array([5., 6., 7., 8.])

分散

分散は、var関数を使いましょう。

np.var(a)
>>実行結果
1.25

標準偏差

標準偏差の算出は、std関数を使います。

np.std(a)
>>実行結果
1.118033988749895

標準偏差や分散がどのような値なのか、何が違うのかについてはこちらの記事で解説しています。


ぜひご参照下さい。

[kanren postid ="567"]

最大・最小

ndarray配列の要素の最大値・最小値を出す場合は、maxとmin関数を使います。

np.max(a)
>>実行結果
4

np.min(a)
>>実行結果
1

行列から抽出する

一次元配列にする

行列を一次元配列にする時は、ravel関数を使います。

ravel関数は、要素を１つずつ取り出したいときに使います。

np.ravel(b)
>array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])

行番号・列番号を指定して抽出する

ndarray配列名[行番号,列番号]と指定することで、指定した要素を取り出せます。

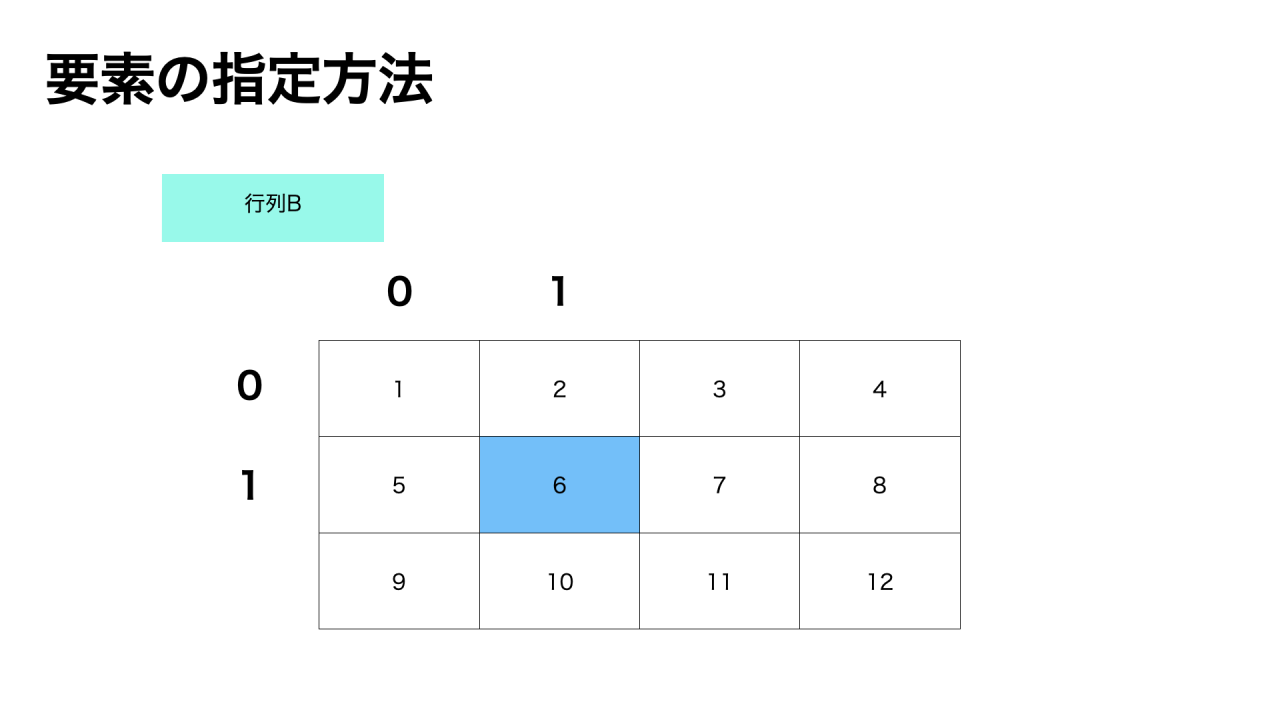
b[1,1]
>>実行結果
6

行番号・列番号は0から始まるので、注意しましょう。

b[0,3]
>>実行結果
4

ベクトルでも番号での指定が可能です。

a[2]
>>実行結果
3

最後の要素を指定したい場合は、-1で指定可能です。

a[-1]
>>実行結果
4

スライスで抽出する

スライスとは、複数要素を取得する場合に範囲選択することです。


スライスには、「:(コロン)」を使います。

#ベクトルの1番目〜2番目を抽出する
a[1:3]
>>実行結果
array([2, 3])

#0行目〜1行目、1列目〜2列目
b[0:2,1:3]
>>実行結果
array([[2, 3],
[6, 7]])

「:（コロン）」は単体で使うと、全選択を意味します。

#行を全選択し、列は列番号で指定
b[:,2]
>>実行結果
array([ 3,  7, 11])

#行は行番号で指定し、列を全選択で指定
b[1,:]
>>実行結果
array([5, 6, 7, 8])

条件で抽出する

条件指定で配列や行列の要素を取得する場合は、比較演算子を使います。

b>4
>>実行結果
array([[False, False, False, False],
[ True,  True,  True,  True],
[ True,  True,  True,  True]])

比較演算子は、次の4種類が使えます。

比較演算子	意味
配列 > x	x よりも大きい要素を取得する
配列 < x	x よりも小さい要素を取得する
配列 >= x	x と等しいか大きい要素を取得する
配列 <= x	x と等しいか小さい要素を取得する

行列を操作する

ベクトル同士の計算

ベクトル同士の計算について学習しましょう。

計算は通常の演算子を使います。

ベクトルの計算方法は、同じ場所にある要素を足したり、引いたりします。

# 計算用の配列を作成
array1 = np.array([1,2,3,4,5,6])
array2 = np.array([2,4,6,8,10,12])
#和
array1 + array2
>>実行結果
array([ 3,  6,  9, 12, 15, 18])

和だけでなく、他の演算でも横方向に計算します。

#差
array2 - array1
>>実行結果
array([1, 2, 3, 4, 5, 6])

#積
array1 * array2
>>実行結果
array([ 2,  8, 18, 32, 50, 72])

#商
array2 / array1
>>実行結果
array([2., 2., 2., 2., 2., 2.])

行列同士の計算

行列の演算も配列と同様に、同じ場所にある要素を足したり、引いたりします。

#行列を作成
matrix1 = np.array([[1,2,3,4,5,6],
                    [2,4,6,8,10,12],
                    [3,6,9,12,15,18]])
matrix2 = np.array([[4,8,12,16,20,24],
                    [5,10,15,20,25,30],
                    [6,12,18,24,30,36]])
#和
matrix1 + matrix2
>>実行結果
array([[ 5, 10, 15, 20, 25, 30],
[ 7, 14, 21, 28, 35, 42],
[ 9, 18, 27, 36, 45, 54]])

#差
matrix2 - matrix1
>>実行結果
array([[ 3,  6,  9, 12, 15, 18],
[ 3,  6,  9, 12, 15, 18],
[ 3,  6,  9, 12, 15, 18]])

#積
matrix1 * matrix2
>>実行結果
array([[  4,  16,  36,  64, 100, 144],
[ 10,  40,  90, 160, 250, 360],
[ 18,  72, 162, 288, 450, 648]])

#商
matrix2 / matrix1
>>実行結果
array([[4. , 4. , 4. , 4. , 4. , 4. ],
[2.5, 2.5, 2.5, 2.5, 2.5, 2.5],
[2. , 2. , 2. , 2. , 2. , 2. ]])

転置

転置とは、行と列を入れ替えることです。

#行と列を入れ替える
b.T
>>実行結果
array([[ 1,  5,  9],
[ 2,  6, 10],
[ 3,  7, 11],
[ 4,  8, 12]])

ただし、ベクトル（一次元配列）は行と列がないため、Tでは転置できません。

#一次元配列は行と列がないため、Tでは転置できない
a.T
>>実行結果
array([1, 2, 3, 4])

行数と列数を指定して形を変える

reshape関数を使うと、行列の行数と列数を変更したり、ベクトルを行列に変更したりすることができます。

#3×4の行列を2×6に変更する
b.reshape(2,6)
>>実行結果
array([[ 1,  2,  3,  4,  5,  6],
[ 7,  8,  9, 10, 11, 12]])

reshape関数を使うと、一次元配列も転置することができます。

もちろん、行列に変換することもできます。

#ベクトルを転置する。（縦1列にする）
a.reshape(4,1)
>>実行結果
array([[1],
[2],
[3],
[4]])

#ベクトルaを2×2の行列に変える
a.reshape(2,2)
>>実行結果
array([[1, 2],
[3, 4]])

ブロードキャスト

ブロードキャストとは、ndarray配列の大きさ・次元が違う場合、自動的に要素をコピーして大きさを揃える機能です。

例えば、ベクトル(一次元配列)と行列(二次元配列)や、スカラー(0次元配列)とベクトルの計算をする際などに効果的です。

#ブロードキャスト（行列と配列の和）
a + b
>>実行結果
array([[ 2,  4,  6,  8],
[ 6,  8, 10, 12],
[10, 12, 14, 16]])

#スカラー（0次元配列）と行列（2次元配列）
5 * b
>>実行結果
array([[ 5, 10, 15, 20],
[25, 30, 35, 40],
[45, 50, 55, 60]])

配列の結合・分割

縦方向にndarray配列を結合する時は、vstack関数を使います。

各行の要素数が同じでないと結合できないので、注意しましょう。

#aとbを縦方向に結合
np.vstack((a,b)) #引数はタプルにすること
>>実行結果
array([[ 1,  2,  3,  4],
[ 1,  2,  3,  4],
[ 5,  6,  7,  8],
[ 9, 10, 11, 12]])

ndarray配列を横方向に結合する時は、hstack関数を使います。

#array1とarray2の確認
array1
>>実行結果
array([1, 2, 3, 4, 5, 6])
array2
>>実行結果
array([ 2,  4,  6,  8, 10, 12])
#array1とarray2を横方向に結合
np.hstack((array1,array2))
>>実行結果
array([ 1,  2,  3,  4,  5,  6,  2,  4,  6,  8, 10, 12])

疑似乱数を生成する

疑似乱数を作る時はrandom関数を使います。

0~1の乱数

random.randで、0~1の乱数を生成できます。

引数には何を入れるのかな？

ベクトルの場合は、生成したい乱数の数（要素数）を入れます。

#ベクトル
np.random.rand(5)
>>実行結果
array([0.85572911, 0.41986047, 0.52022084, 0.60679373, 0.02879198])
where

行列の場合の引数は、(行,列)で指定します。

#行列
np.random.rand(4,6)
>>実行結果
array([[0.35599728, 0.14748427, 0.86172026, 0.92575276, 0.29228079,
0.22964651],
[0.34756348, 0.08573972, 0.59858781, 0.67060099, 0.00791902,
0.02872533],
[0.82821718, 0.75247201, 0.8961799 , 0.94816615, 0.48520699,
0.15950374],
[0.94662943, 0.81549464, 0.1551827 , 0.84437122, 0.20545317,
0.96384743]])

指定した範囲の整数の乱数

指定した範囲にある整数をランダムに選んで、ベクトルや行列を作りたい場合は、random.randintを使います。

#引数の数字以内で整数を1つ選ぶ
np.random.randint(30)
>>実行結果
13

#範囲指定（10~30）
np.random.randint(10,30)
>>27

#複数の乱数を生成する（ベクトル）
np.random.randint(10,30,6)
>>実行結果（要素数=6）
array([18, 17, 20, 21, 24, 25])

#複数の乱数を生成する（行列）
np.random.randint(10,30,(6,3))
>>実行結果
array([[21, 27, 22],
[16, 28, 11],
[10, 28, 28],
[19, 27, 10],
[27, 10, 28],
[28, 19, 12]])

最後に

Pythonでデータ分析・データサイエンスをしたい初心者向けに、Pythonデータ分析徹底解説総まとめページを作成しました。

流れに沿って実装することで、データ分析の基礎が固められます。