今回はkintoneの標準機能の数式を使って自然対数ln(X)を求めます。
このln(X)、数学では
\ log_eX\\
\ logX\\
のように書かれますね。
「ろぐいーていえっくす」のように読まれるやつです。
プログラミングの世界ではlogではなくてlnを使うようです。
というわけで、kintoneの標準機能で自然対数の近似をしてみたいと思います。
計算方法
ln0は定義されておらず
X=0の周りのマクローリン展開をすることができません。
そこで、X=x+1 とおいて、ln(x+1)をx=1でテイラー展開すると
\ -1<x\leqq1 のとき\\
\ln(x+1) = x -\frac{x^2}{2} +\frac{x^3}{3} - \frac{x^4}{4} + ・・・\\
のような多項式に近似することができます。
※詳しくは以下をご参照ください。
これを利用して、たとえば以下のように近似したいと思います。
\ -1<x\leqq1 より0<X\leqq2 \\
\ X=1.5 のとき\\
\ x = 1.5 - 1 = 0.5 なので\\
\ lnX = ln1.5 = ln(0.5+1) = 0.5 -\frac{0.5^2}{2} +\frac{0.5^3}{3} - \frac{0.5^4}{4} + ・・・\\
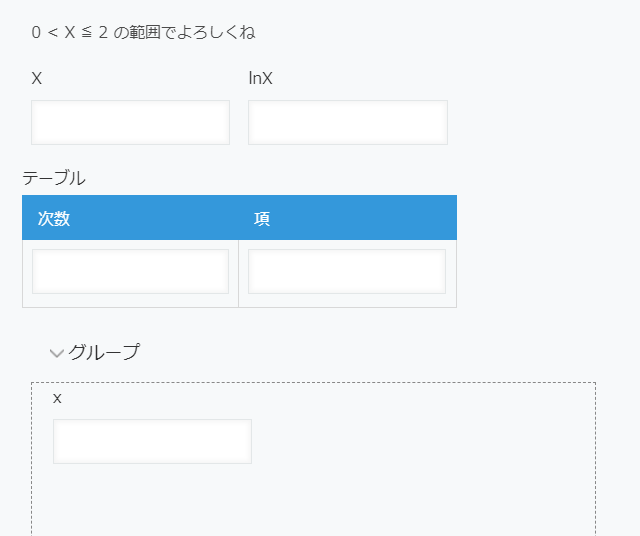
アプリの準備
アプリ自体は結構シンプル。
アプリ名はlnX(0<X≦2)を求めるアプリとしておきましょう。
※あとでルックアップしてくるときに使います。
| フィールド種類 | フィールドコード | 数式 | 備考 |
|---|---|---|---|
| 数値 | X | ||
| 計算 | lnX | SUM(項) | |
| 数値 | 次数 | テーブル内フィールド手入力が大変だけど1から100まで行作ってね。 | |
| 計算 | 項 | 後述 | テーブル内フィールド |
| 計算 | x | X-1 | グループ内に隠してもOK |
計算フィールドの「項」の数式はこんなかんじ。
(-1)*(-x)^次数/次数
+(-1)*(-x)^次数*(-x)^100/(次数+100)
+(-1)*(-x)^次数*(-x)^100*(-x)^100/(次数+200)
+(-1)*(-x)^次数*(-x)^100*(-x)^100*(-x)^100/(次数+300)
+(-1)*(-x)^次数*(-x)^100*(-x)^100*(-x)^100*(-x)^100/(次数+400)
+(-1)*(-x)^次数*(-x)^100*(-x)^100*(-x)^100*(-x)^100*(-x)^100/(次数+500)
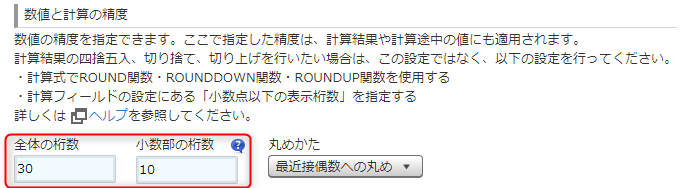
有効桁数の設定
アプリの設定で、その他の設定→高度な設定の
数値と計算の精度の桁数は
全体の桁数：30
小数部の桁数：10
にしておきましょう。
使い方
準備：テーブル行を追加して次数フィールドに1～100まで入力します。（csvなど読み込ませてもいいかも）
準備ができたらXに0より大きくて2以下の値を入力すると、lnXフィールドに計算結果が表示されます。
近似値なのでピッタリ！というわけにはいかないけど近い値が計算結果が表示されます。
別の計算がしたくなった場合は、テーブル内の入力が面倒なので
新規レコードを追加するのではなく、「レコードの再利用」をして計算してね。
実際に計算してみた動画コチラ↓