突然ですが、問題です!
次の表は、あるお菓子屋さんのケーキのレシピだとします。
| チーズケーキ | チョコケーキ | ||
|---|---|---|---|
| 利益 | 500円/個 | 200円/個 | 材料在庫 |
| 材料1:たまご | 30g/個 | 20g/個 | 2,400g |
| 材料2:砂糖 | 40g/個 | 10g/個 | 2,500g |
チーズケーキを1つ作るためには、たまごが30g、砂糖が40g必要です。
また、チーズケーキ1つ売ったら利益が500円です。
チョコケーキを1つ作るためには、たまごが20g、砂糖が10g必要です。
チョコケーキを1つ売ったら利益が200円です。
たまご、砂糖はそれぞれ在庫に限りがあって、
たまごは全部で2,400g、砂糖は2,500gです。
お菓子屋さんは、この限りある在庫をフルに使って、チーズケーキとチョコケーキを作って売ります。
そのとき、チーズケーキを何個、チョコケーキを何個作れば利益が最大になるでしょう👀!?
※作ったケーキは全部売れるものとします
とりあえず手計算してみる(計算失敗パターン)
先程の表です。
| チーズケーキ | チョコケーキ | ||
|---|---|---|---|
| 利益 | 500円/個 | 200円/個 | 材料在庫 |
| 材料1:たまご | 30g/個 | 20g/個 | 2,400g |
| 材料2:砂糖 | 40g/個 | 10g/個 | 2,500g |
表を見た感じ、チーズケーキの利益は1個あたり500円、チョコケーキの利益は1個あたり200円です。
チーズケーキを売ったほうが利益が高そうなので、チーズケーキを在庫が許す限り最大数作ってみましょう。
チーズケーキは最大何個作れるか
チーズケーキを1つ作るために、たまごは30g、砂糖は40g必要です。
たまごと砂糖の在庫からどれだけ作れるか計算すると
たまご: $ 2400 \div 30 = 80 $
砂糖:$ 2500 \div 40 = 62 あまり20 $
つまり、卵は80個分、砂糖は62個分作れる量あります。
たまごに合わせてチーズケーキを80個も作ろうとすると砂糖が足りなくなるので、
62個作るようにしましょう。
チーズケーキを62個作ると、卵と砂糖の在庫はそれぞれ
たまご: $2400 - 30 \times 62 = 540g $
砂糖: $ 20g $
だけ、余ります。
チョコケーキを1つ作るためには、たまごが20g、砂糖が10g必要です。
すると残った材料でチョコケーキは2つ作れます。
最終的に余る材料は
たまご: $ 540 - 20 \times 2 = 500g $
砂糖: $ 20 - 10 \times 2 = 0g $
となります。
利益はチーズケーキ1個あたり500円、チョコケーキ1個あたり200円なので
$ 500 \times 62 + 200 \times 2 = 31400円 $
31,400円の利益が出ます。
しかしこれは最大の利益とはなりません。
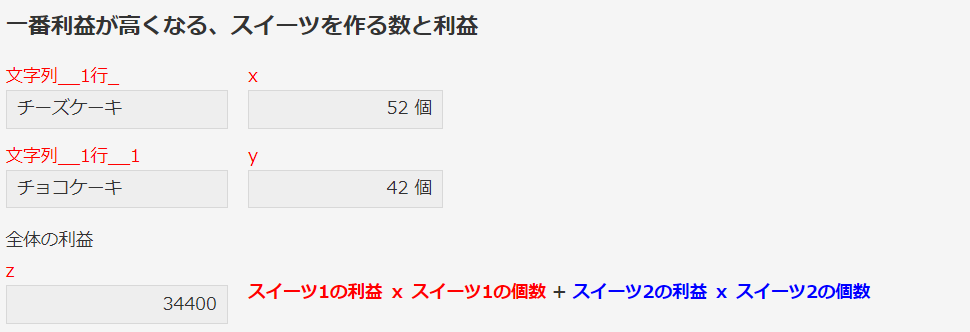
答えを先に言ってしまうと
チーズケーキ:52個
チョコケーキ:42個
のとき
利益:34,400円(最大)
となります。
前置きが長くなりましたが、今回はこういった条件が与えられたときの、最大の利益を求めるアプリを
kintoneで作ってみたいと思います。
計算方法よりアプリを作りたい!という方は、アプリの準備まで飛んでね!
問題を解く方針
またまた、先程の表です。
| チーズケーキ | チョコケーキ | ||
|---|---|---|---|
| 利益 | 500円/個 | 200円/個 | 材料在庫 |
| 材料1:たまご | 30g/個 | 20g/個 | 2,400g |
| 材料2:砂糖 | 40g/個 | 10g/個 | 2,500g |
チーズケーキ:□個
チョコケーキ:△個
のとき、
利益を最大にしたい。
ということで、
チーズケーキを$ x $個、チョコケーキを$ y $個作ったときの利益$ z $を最大にする
という問題に置き換えて計算を進めていきます。
チーズケーキをx個、チョコケーキをy個作ったときの利益zを数式で表す
何回出てくるんだという感じですが先程の表です。
| チーズケーキ(x個) | チョコケーキ(y個) | ||
|---|---|---|---|
| 利益(z) | 500円/個 | 200円/個 | 材料在庫 |
| 材料1:たまご | 30g/個 | 20g/個 | 2,400g |
| 材料2:砂糖 | 40g/個 | 10g/個 | 2,500g |
たまごについて注目すると、
チーズケーキをx個、チョコケーキをy個作るとたまごの使用量は
$ 30 \times x + 20 \times y $となります。
これは在庫の2400g以下である必要があるため、xとyの式で表すと
たまごについて:$ 30x + 20y \leqq 2400 $ ---①
となります。
同様に砂糖については
砂糖について:$ 40x + 10y \leqq 2500 $ ---②
となります。
利益(z)についてはx, y, z の式で表して
$ z = 500x + 200y $ ---③
となります。
①、②、③はそれぞれx-y平面の直線グラフで表すことができます。
まずは①たまごの直線と②さとうの直線について直線のグラフを書くと下図のようになります。
緑色で塗っているのは、
①も②も不等式で、また、$ x\geqq 0 , y \geqq 0$であり、不等式を満たす範囲を塗っている・・・ということです。

これに③利益(z)のグラフ(赤)を並べると下図のようになります。
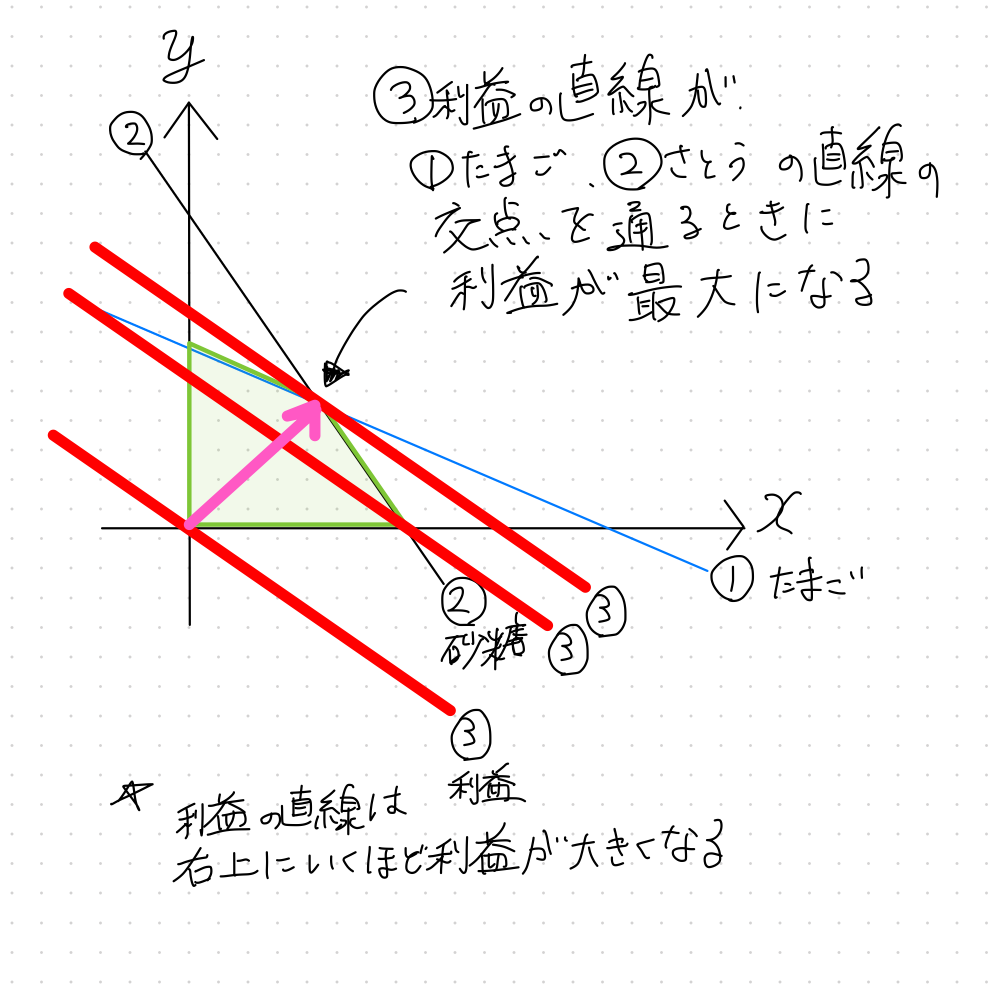
緑色で囲まれた部分の中で、③利益の直線が一番右上にあるときに、
利益の値が最大となります。
図より、利益の値が最大となるのは③利益(z)のグラフが①たまごと②砂糖のグラフの交点を通るときとなるので
①と②の交点の座標(x, y)がわかれば③の式に(x, y)を代入して、最大の利益を求めます。
①たまご直線と②砂糖直線の交点を求める
交点を求めるには、下記の連立方程式を解きます。
①たまご直線の式:$ 30x + 20y = 2400 $
②砂糖直線の式:$ 40x + 10y = 2500 $
①の両辺を20で割って:$ \frac{3}{2} x + y = 120 $ ---①'
②の両辺を10で割って:$ 4x + y = 250$---②'
②' - ①'を計算して
$ \frac{5}{2}x =130 $
$ x = 52 $
②'に代入して
$ 4 \times 52 + y = 250$
$ y = 42 $
③に代入して
$ z = 500 \times 52 + 200 \times 42 = 34400 $
というわけで答え
チーズケーキ:52個
チョコケーキ:42個
のとき
利益:34,400円(最大)
となります。
このような解き方を線形計画法といいます。
アプリの準備
計算の流れを説明したところで、ここからようやくkintoneアプリを作っていきます。
条件入力部分
例の表の条件を入力する部分を作ります。
どれがフィールド名でどれがフィールドコードで、どれがフィールド種類か?は画像上で読み取ってね!
このあたりは全部手入力です。

計算結果表示部分
文字列__1行_と文字列__1行__1はスイーツ名表示用です。フィールド名もフィールドコードも何でも良いです。
| フィールド種類 | フィールドコード | 計算式 |
|---|---|---|
| 文字列(1行) | 文字列__1行_ |
スイーツ1 |
| 文字列(1行) | 文字列__1行__1 |
スイーツ2 |
| 計算 | x | 後述 |
| 計算 | y | 後述 |
| 計算 | z | rieki1x+rieki2y |
計算フィールドxの計算式
IF(判定="切1",
切1x,
IF(判定="x交1",
x交1x,
IF(判定="切2",
切2x,
交12x
)
)
)
計算フィールドyの計算式
IF(判定="切1",
切1y,
IF(判定="x交1",
x交1y,
IF(判定="切2",
切2y,
交12y
)
)
)
途中計算部分
解き方の説明では省略しましたが、
実は、①、②、③の直線の傾きの関係によってどこが最大の利益となるか変わってきます。
いつも①と②の交点が最大の利益の点となるわけではありません。
(利益の直線のy切片が最大になるときに利益最大となります。)
x,y両方正の値じゃないところに交点があるとき(交点が第1象限にないとき)

利益直線の傾きが①と②の傾きよりも急だったりゆるやかだったりするとき
交点のx,yがどちらも正の値でも、利益直線の傾きによって、交点が最大の利益になる点ではない場合もあります。
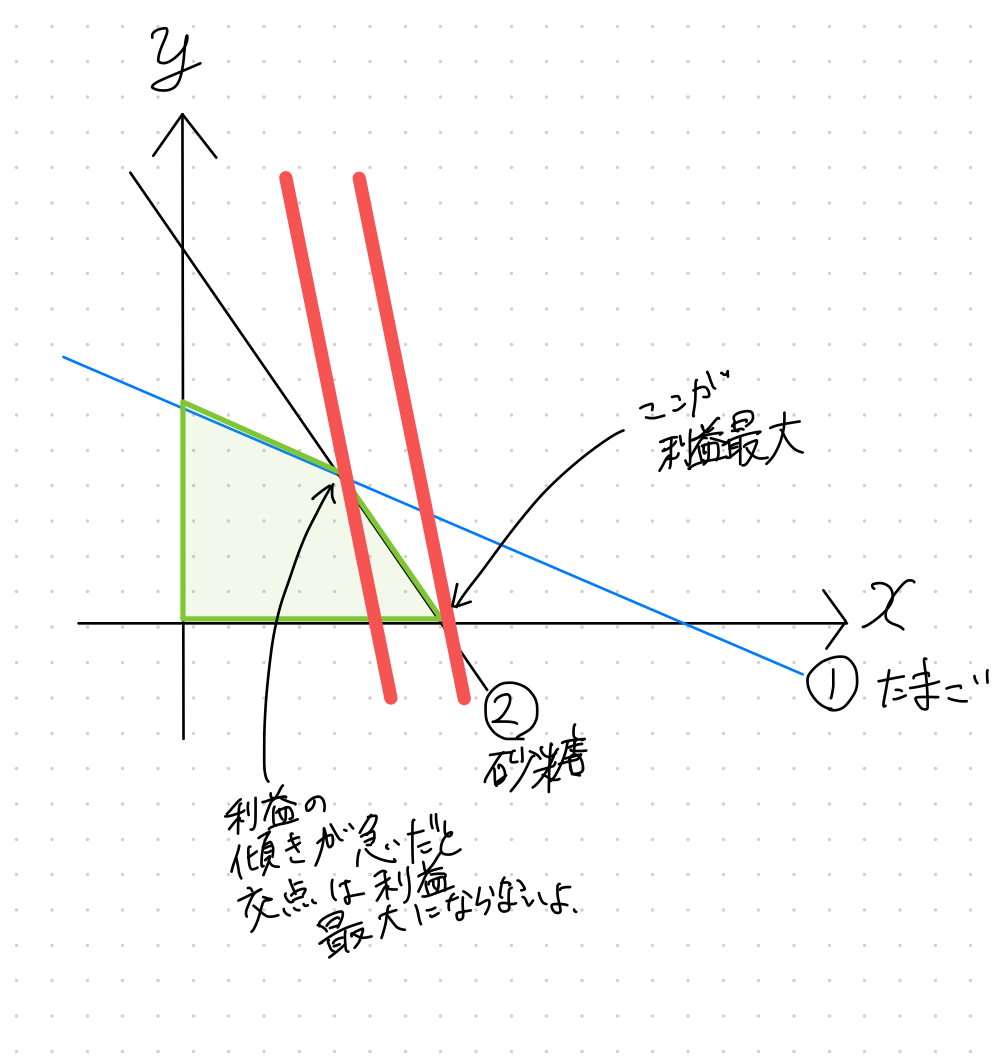
途中計算では場合分けをする
①と②の交点以外の点が最大の利益になる点についても場合分けして計算しています。
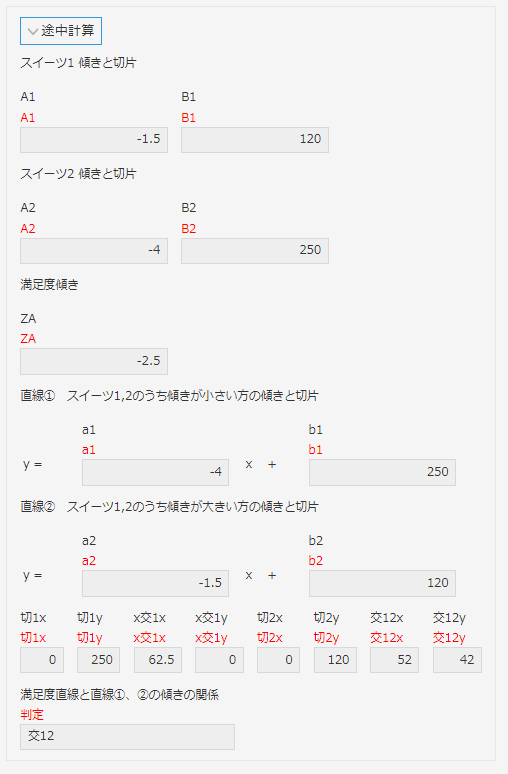
| フィールド種類 | フィールドコード | 表している内容 | 計算式 |
|---|---|---|---|
| 計算 | A1 | 直線①の傾き | -a11/a12 |
| 計算 | B1 | 直線①のy切片 | zaiko1/a12 |
| 計算 | A2 | 直線②の傾き | -a21/a22 |
| 計算 | B2 | 直線②のy切片 | zaiko2/a22 |
| 計算 | ZA | 利益直線の傾き | -rieki1/rieki2 |
| 計算 | a1 | ①と②の傾き大きい方の直線①'の傾き | IF(A1<=A2,A1,A2) |
| 計算 | b1 | ①と②の傾き大きい方の直線①'のy切片 | 後述 |
| 計算 | a2 | ①と②の傾き小さい方の直線②'の傾き | IF(A1<=A2,A2,A1) |
| 計算 | b2 | ①と②の傾き小さい方の直線②'のy切片 | 後述 |
| 計算 | 切1x | ①'のy切片のx座標(当然0だけど) | 0 |
| 計算 | 切1y | ①'のy切片のy座標 | b1 |
| 計算 | x交1x | ①'とx軸の交点のx座標 | -b1/a1 |
| 計算 | x交1y | ①'とx軸の交点のy座標(当然0だけど) | 0 |
| 計算 | 切2x | ②'のy切片のx座標(当然0だけど) | 0 |
| 計算 | 切2y | ②'のy切片のy座標 | b2 |
| 計算 | 交12x | ①と②の交点のx座標 | (b2-b1)/(a1-a2) |
| 計算 | 交12y | ①と②の交点のy座標 | a1*交12x+b1 |
| 文字列(1行) | 判定 | 利益最大になるのはどのパターンか判定している | 後述 |
b1の計算式
IF(A1=A2,
IF(B1<=B2,B1,B2),
IF(A1<A2,B1,B2)
)
b2の計算式
IF(A1=A2,
IF(B1<=B2,B2,B1),
IF(A1<A2,B2,B1)
)
判定の計算式
IF(a1=a2,
IF(a1<=ZA,
"切1",
"x交1"
)
,
IF(ZA<=a1,
"x交1",
IF(a2<=ZA,
"切2",
"交12"
)
)
)
使い方動画
材料の条件や利益について入力すれば、それぞれ何個作れば利益が最大になるか自動計算されます。
まとめ
簡単な線形計画法の問題だったらkintoneの標準機能でも、なんとか解くことができます。
なにかに応用できるといいなぁと思います。