背景と目的
Haskell Advent Calendar 2018 4日目の記事です。
もう少しHaskellの話題に触れたかったので力及ばず申し訳ないです。
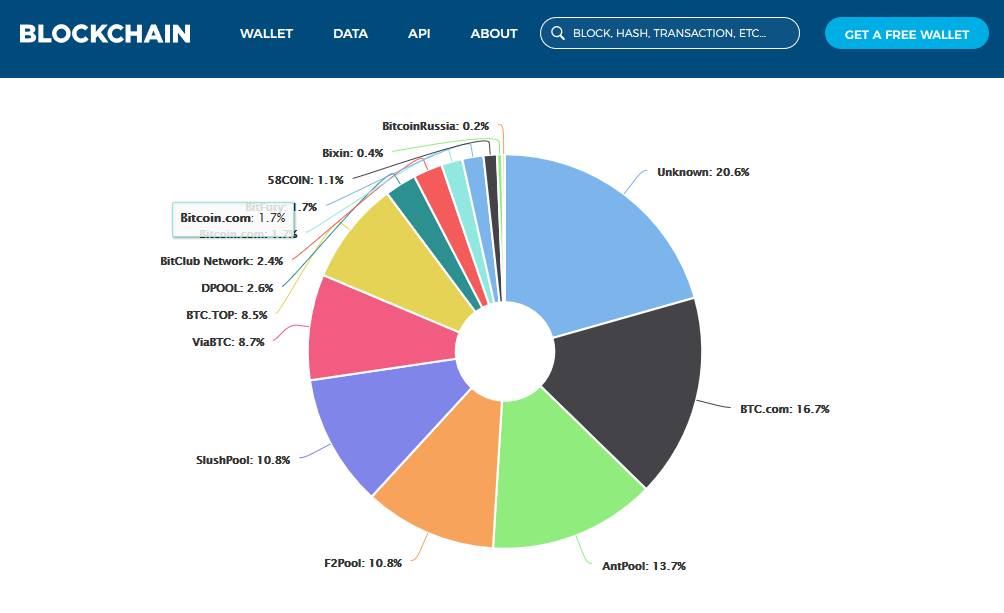
話題のブロックチェーンであるビットコインですが、オープンなデータベース上で2重支払いをできないようにするためにみんなの計算機のパワー(POW)で独裁者がでないようにしているところがすごいですね。
実際には10%以上握っているマイナーがいます。特にbitmain社のAntPoolはASICマイナーです。
最近売り出し中のものはbitmain社のs9iで14.5TH/sでます。どういうテクノロジーならここまでいけるのか、また超えることはできるのか推測しました。考察の結果51%を大幅に超えることができば2重支払いや新しいコインをほとんど集められることでしょう。
bitmain社のs9iはASICマイナーでそのパワーは?
bitmain社のs9iはASICマイナーです。ASICがGPUやCPUよりはるかに強いのは命令のためのメモリをもたず、演算器の使用率を100%引き出すことができる点です。
IntelのCPUではCPUに比べメモリは遅いのでハイパースレッディングやマルチコアを利用して演算器が遊ばないように工夫されていますが限界があります。
ASICマイナーは1サイクルに1ハッシュのスループットを出すのが容易です。
bitcoinのハッシュはSHA256ですが、掛算もなくメモリへのアクセスも不要なため回路も小さく作れます。10段程度のパイプラインで作って、雑に見積もると256bit x 3 x 10 x 10 = 76kgate程度でしょうか。これは8bitマイコン程度で大変小さいです。
これを1Ghzで動かすと1GH/sですね。
s9iは一台に189個のASICを詰めているそうです。
最新のAppleのA11では4.3Bトランジスタだそうなので一チップで14TH/s(下記にて計算)いけそうです。
4.3*(1000^3)/(4*76800) = 14 TH/s
何チップあれば51%とれるか?
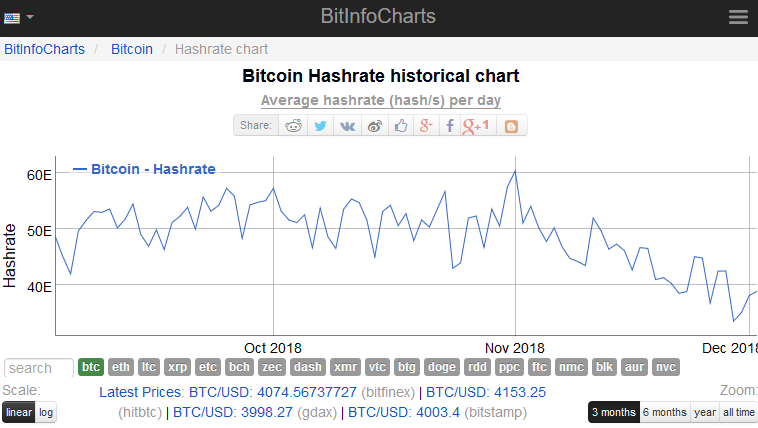
14TH/sでるチップがいくつあれば51%とれるでしょうか、bitcointのhashrateは40EH/sなのでおよそ290万個あればとれそうです。(下記にて計算)
(40*1000*1000)/(14)= 290万個
290万個なので一チップ千円でつくることができれば29億円で51%とれそうですね。
どうやってASICつくるの?
ようやく本題でどうやってASICつくるのかです。もちろんHaskellです。
まず、Haskellでbitcoinを既存の実装にならって実装します。
こちらの記事をみてHaskell版をつくります。おそらく本当のbitcoinとはなにかが違う気もしますがこの際気にしないことにします。
次にPOWの肝であるハッシュのプログラムをHaskellで書き直します。
Crypto.HashはC言語で書かれているのでそれを参考にしてHaskell版を作成します。
Haskell版のハッシュ計算のプログラムをClashにかけVerilog版をつくります。
これは段数が一段だけなので1GHzで動作することはできないです。高速化は次回の課題にします。
まとめ
bitcoinのASICマイナーの簡単な紹介とHaskellによるASICマイナー作成のトライアルを行いました。また51%をとるために必要なASICの個数をざっくり見積もってみました。