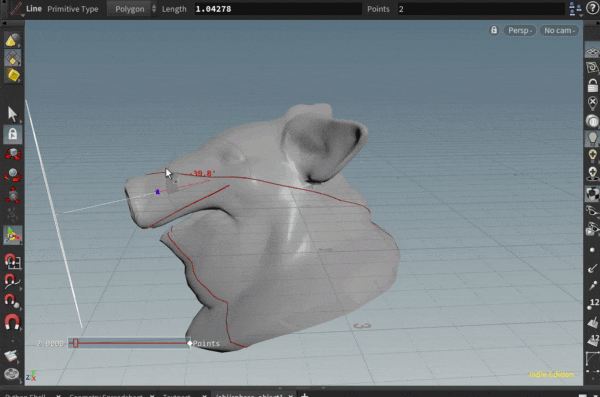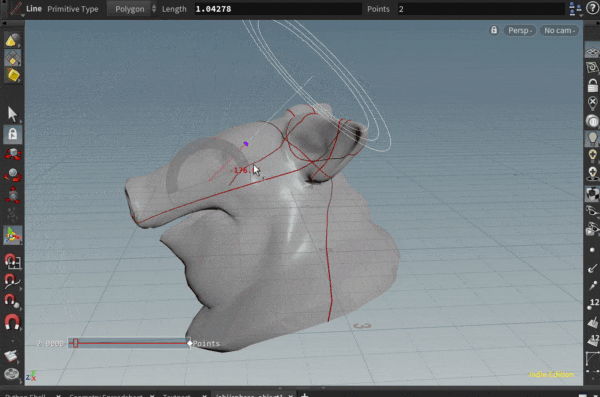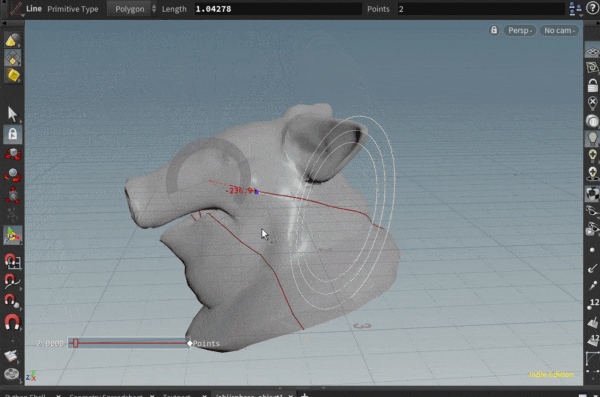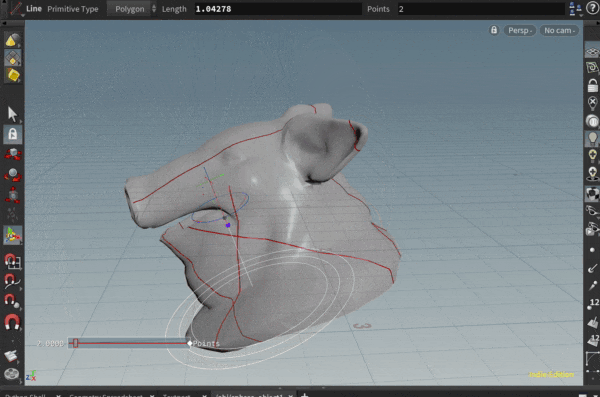
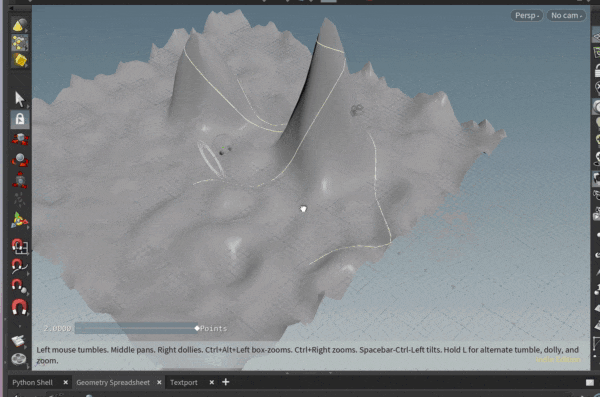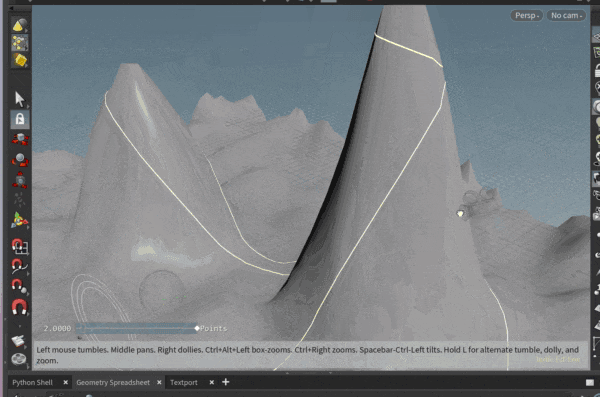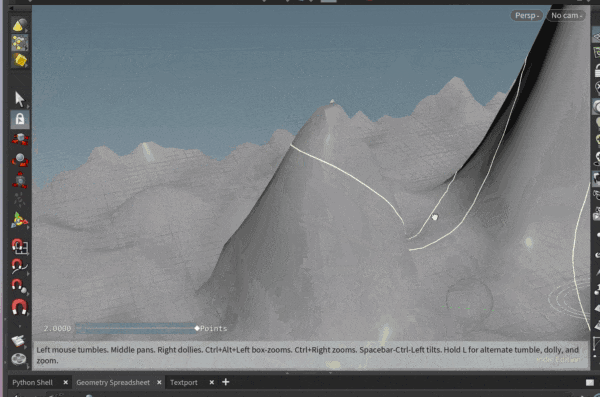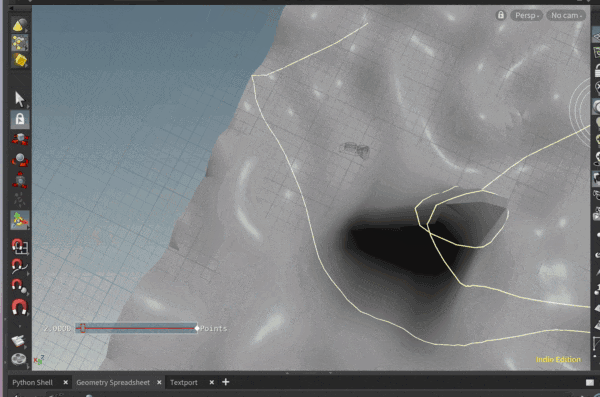
ポリゴンオブジェクト上の面に沿って、直線を引きたいと思ったことはありませんか？
そんなときには測地線という概念が役立ちます。
雰囲気重視の記事ですので、未定義語やいい加減な解説が受け付けない方は参考資料の方を読んで頂けると良いと思います。
測地線とは
一言で雑に言えば、滑らかな曲面上での真っ直ぐな線のことです。曲面からどう線を引いても、ユークリッド空間(直交座標)で見たら曲線になってしまうので、直線ではないのですが。
地球上の2点を結ぶ最短距離に「大圏航路」と呼ぶのを聞いたことがないでしょうか。2点と地球の中心を通る平面で地球を切ったときに出来る大円がそれです。大圏航路は球面上の測地線です。
身体感覚で言うと、測地線は真っ直ぐ歩いたときの軌跡のことを指します。
東京から真東にまっすぐ歩きはじめると、大圏航路になり、だんだん南に進路を取り、南米を通って東京に戻ってきます。
緯度を一定にしようと(東に進み続けようと)したら、やや左に曲がりながら歩くことになります。東京近辺で考えると曲がり加減が僅かですが、北極付近で同じことをしようとしたらかなり左に曲がらなければ東に進み続けられないのが想像できるでしょう。
地球の場所を緯度経度で表すことを、座標を導入すると言いますが、本来、地球は単なる球であって座標のとり方で真っ直ぐ歩いたときの軌跡が変わったりしないはずです。
座標のとりかたに依存しないように気をつけた共変微分だったりします。
曲面上でのベクトルの平行移動
平面上で直線が持つ性質を考えてみましょう。色々あるとは思いますが、直線に沿った方向ベクトルをどれだけ直線に沿って平行移動しても変化しない、というものが測地線にとっては重要です。
レヴィ・チヴィタ接続・共変微分
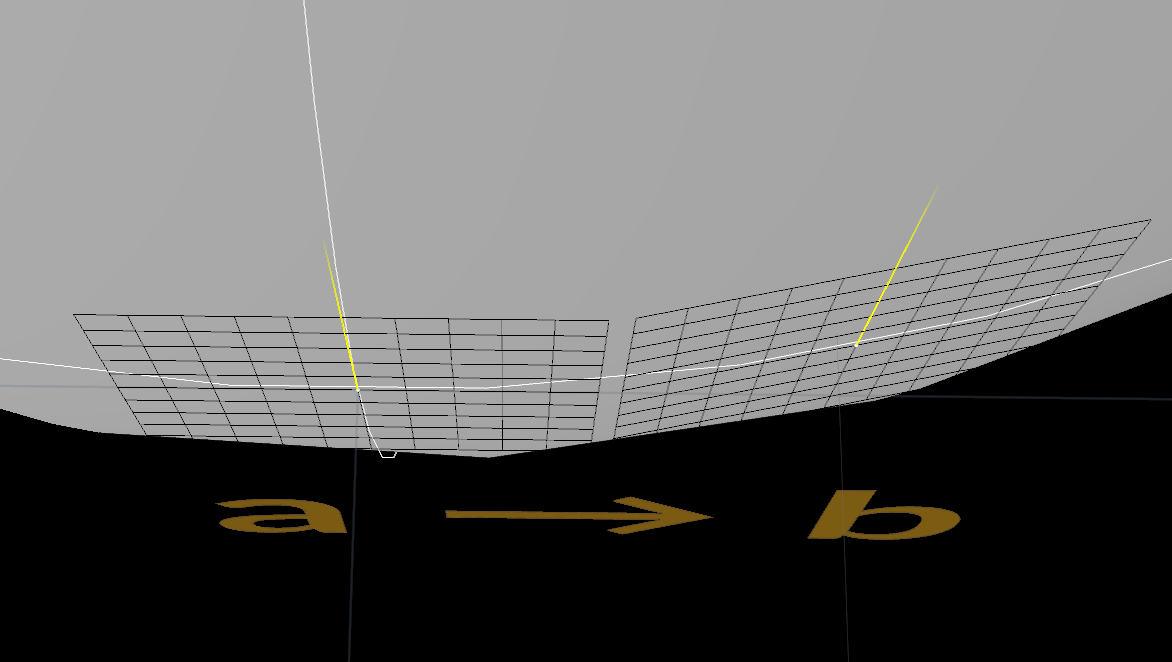
でも、曲面上でどのようにベクトルの平行移動を定義すればいいのでしょうか。曲面上の曲線に従っての平行移動を考えますが、以下のように、ユークリッド空間での平行移動では、曲面の接平面からベクトルが飛び出てしまう場合があります。
飛び出さないケース
点a上の上方向のベクトルをそのまま点bに平行移動しても接平面から飛び出していません。飛び出すケース
点a上の右方向のベクトルをそのまま点bに平行移動すると接平面から飛び出してしまいます。
平行移動の最中に飛び出てしまった場合は、飛び出た分は曲面に接する平面に射影する、と考えるのがレヴィ・チヴィタ接続における共変微分を考慮したベクトルの平行移動です。
- 射影してみる
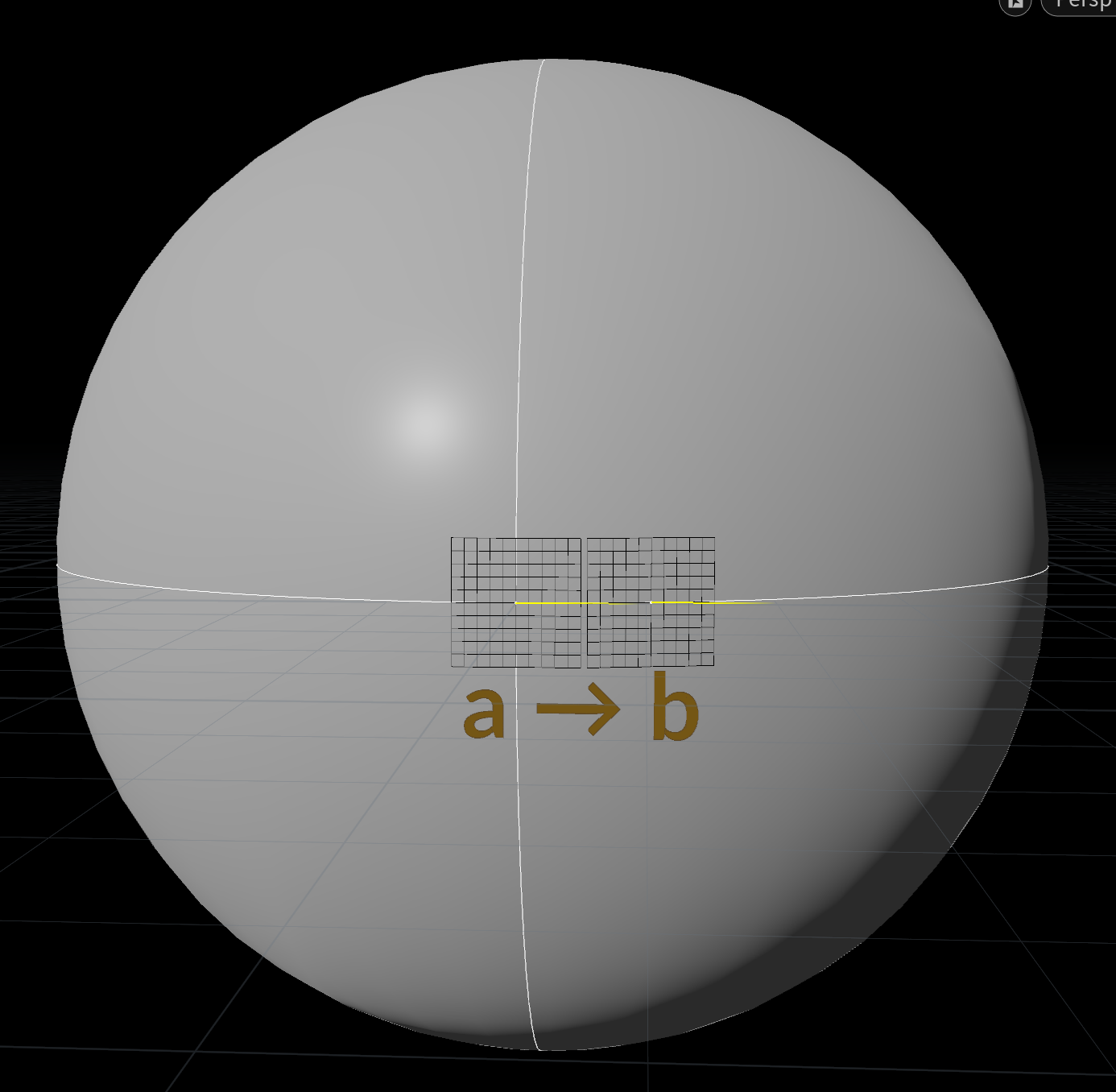
点a上の右方向のベクトルをそのまま点bに平行移動したあと、接平面に対して射影したベクトルが青いベクトルです。当然接平面から飛び出していません。
ちなみに、ベクトルの平行移動は以下の例からわかるように経路に依存しており、スタート地点、ゴール地点、スタート時のベクトルが一緒でも経路が異なると一致しません。
点a→点cに直接行く(黄色ベクトル)のと、点aから点bを経由して点cに行く(緑色ベクトル)のでは、どちらもベクトルを平行移動させたはずなのに点cでのベクトルが90°違う方向を向いていることがわかると思います。
共変微分をやってみる
共変微分は、まず、適当な座標系を決めるところから始めます。
球面上での共変微分を試してみます。半径 $ r = 1 $の球面座標系を以下のようにとります。
\begin{align}
x &= \cos x^0 \\
y &= \sin x^0 \cos x^1 \\
z &= \sin x^0 \sin x^1
\end{align}
ある点 $ p = (x^0, x^1) $ 上での基底ベクトル(ローカルな座標系を示すものです)は、以下のようになります。
\begin{align}
\boldsymbol{e}_{x^0} &= \frac{\partial }{\partial x^0} (x, y, z) \\
&= (-\sin x^0, \cos x^0\cos x^1, \cos x^0 \sin x^1) \\
\boldsymbol{e}_{x^1} &= \frac{\partial }{\partial x^1} (x, y, z) \\
&= (0, -\sin x^0 \sin x^1, \sin x^0 \cos x^1)
\end{align}
これらの基底ベクトル $ \boldsymbol{e}_{x^0} $ , $ \boldsymbol{e}_{x^1} $ が、$ x^0 $ , $ x^1 $ が変化したときにどのように変化するかをまた基底ベクトル$ \boldsymbol{e}_{x^0} $ , $ \boldsymbol{e}_{x^1} $で表すのが共変微分なのですが、基底ベクトルをユークリッド座標で表現しているときは、以下の式で計算できます。( $ \boldsymbol{n} $ は、曲面から飛び出す成分です)
\begin{align}
\nabla_{\boldsymbol{e}_{x^0}}\boldsymbol{e}_{x^0} = \lim_{\Delta x^0 \rightarrow 0} \frac{\boldsymbol{e}_{x^0}}{\Delta x^0} &= (-\cos x^0, -\sin x^0 \cos x^1, -\sin x^0 \sin x^1) \\
&= 0 \boldsymbol{e}_{x^0} + 0 \boldsymbol{e}_{x^1} + \boldsymbol{n} \\
\nabla_{\boldsymbol{e}_{x^0}}\boldsymbol{e}_{x^1} = \lim_{\Delta x^0 \rightarrow 0} \frac{\boldsymbol{e}_{x^1}}{\Delta x^0} &= (0, -\cos x^0 \sin x^1, \cos x^0 \cos x^1) \\
&= 0 \boldsymbol{e}_{x^0} + \cot x^0 \boldsymbol{e}_{x^1} \\
\nabla_{\boldsymbol{e}_{x^1}}\boldsymbol{e}_{x^0} = \lim_{\Delta x^1 \rightarrow 0} \frac{\boldsymbol{e}_{x^0}}{\Delta x^1} &= (0, -\cos x^0 \sin x^1, \cos x^0 \cos x^1) \\
&= 0 \boldsymbol{e}_{x^0} + \cot x^0 \boldsymbol{e}_{x^1} \\
\nabla_{\boldsymbol{e}_{x^1}}\boldsymbol{e}_{x^1} = \lim_{\Delta x^1 \rightarrow 0} \frac{\boldsymbol{e}_{x^1}}{\Delta x^1} &= (0, -\sin x^0 \cos x^1, -\sin x^0 \sin x^1) \\
&= -\cos x^0 \sin x^0 \boldsymbol{e}_{x^0} + 0 \boldsymbol{e}_{x^1} + \boldsymbol{n}
\end{align}
ちなみに、微分した結果から基底ベクトルの係数と $ \boldsymbol{n} $ を機械的に計算するには、微分したものと基底ベクトルの内積をとる必要があります。
これらをまとめてクリストッフェル記号 $ {\Gamma^k}_{ij} $ で表すことが一般的のようで、
\nabla_{\boldsymbol{e}_{x^i}}\boldsymbol{e}_{x^j} = \sum_{k} {\Gamma^k}_{ij} \boldsymbol{e}_{x^k}
と書けます。
クリストッフェル記号 $ {\Gamma^k}_{ij} $ でまとめると、
{\Gamma^0}_{00} = 0 \qquad {\Gamma^1}_{00} = 0 \\
{\Gamma^0}_{01} = 0 \qquad {\Gamma^1}_{01} = \cot x^0 \\
{\Gamma^0}_{10} = 0 \qquad {\Gamma^1}_{10} = \cot x^0 \\
{\Gamma^0}_{11} = -\cos x^0 \sin x^0 \qquad {\Gamma^1}_{11} = 0 \\
となります。
基底ベクトル、共変微分を可視化してみると以下の図のようになります。
余談ですがLaTeXを書いたらHoudini上でタイプセッティングしてくれるPythonノードがほしいです。
平行移動をやってみる
$\boldsymbol{Z} = (Z^0, Z^1)$ をベクトル場とします。曲線が $ \boldsymbol{p}(t) = (x^0,x^1) = (p^0(t), p^1(t)) $ で表されるとします。いろいろ計算すると
\nabla_{\boldsymbol{\dot p} (t)} \boldsymbol{Z} = \left( \dot Z^k + \dot p^i(t) Z^j {\Gamma^k}_{ij} \right)\boldsymbol{e}_k = 0 \\
ここで\\
\boldsymbol{Z} = \boldsymbol{Z}(\boldsymbol{p}(t)) = \left(Z^0(\boldsymbol{p}(t)), Z^1(\boldsymbol{p}(t))\right) \\
\dot Z^k = \frac{\mathrm{d}}{\mathrm{d}t}Z^k(\boldsymbol{p} (t))
となり、これが曲線上の点 $\boldsymbol{p}(t)$ における $\boldsymbol{Z}$ の平行移動を満たす変換規則になります。
測地線の方程式
初めに( $ t = 0 $ )、曲面上にスタート地点 $ \boldsymbol{p}(0) $ と、行きたい方向 $ \boldsymbol{\dot p}(0) = {\Large{\frac{\mathrm{d} \boldsymbol{p}}{\mathrm{d} t}}}(0) $ を決めます。
$ \boldsymbol{p}(0) + \Delta \boldsymbol{\dot p} (0) $ 、つまり、スタート地点からわずかに $ \boldsymbol{\dot p}(0) $ 方向に進んだ場所で、進行方向 $ \boldsymbol{\dot p}(0) $ が平行移動されているはずです。
一般的に、$ \boldsymbol{p}(t) $ 周辺でも同様のことが起こっているはずなので、平行移動の式 $ \boldsymbol{Z} $ に $ \boldsymbol{\dot p}(t) $ を代入してみます。
\nabla_{\boldsymbol{\dot p} (t)} \boldsymbol{\dot p} (t) = \left( \ddot p^k(t) + {\dot p}^i(t) {\dot p}^j(t) {\Gamma^k}_{ij} \right)\boldsymbol{e}_k = 0
つまり
\ddot p^k(t) + {\dot p}^i(t) {\dot p}^j(t) {\Gamma^k}_{ij} =0
書き方を変えたら
\frac{\mathrm{d}^2 p^k}{\mathrm{d} t^2} + {\Gamma^k}_{ij} \frac{\mathrm{d}p^i}{\mathrm{d}t} \frac{\mathrm{d}p^j}{\mathrm{d}t} = 0
が測地線の方程式ということになります。
ポリゴン上での近似
ぶっちゃけ、ポリゴン上で測地線を近似するなら、平行移動や測地線の方程式をちゃんと理解していなくても問題ありません。
大事なのは平行移動がベクトルの射影で定義されるということなので、
ポリゴン上では方向ベクトルに従って進んで、ポリゴンのエッジに当たったら隣のポリゴンに対して射影さえとってやれば同じような結果が得られます。
もっと言うと、ポリゴンのエッジ回りの法線の角度差を計算して、エッジを軸に回す方が良いです。射影だと90°以上の角度が付いている場合にうまくいかないのです。
ということで、そのような計算をVEXでゴリゴリして、
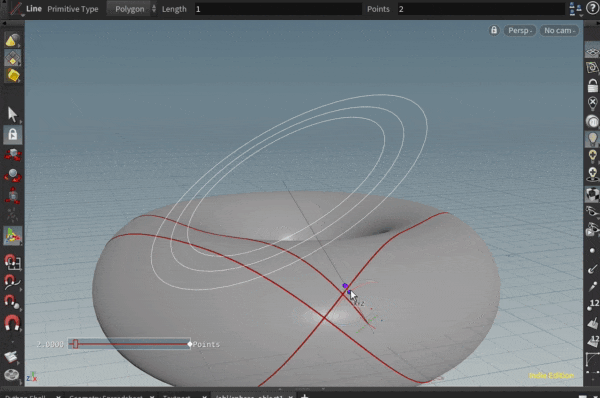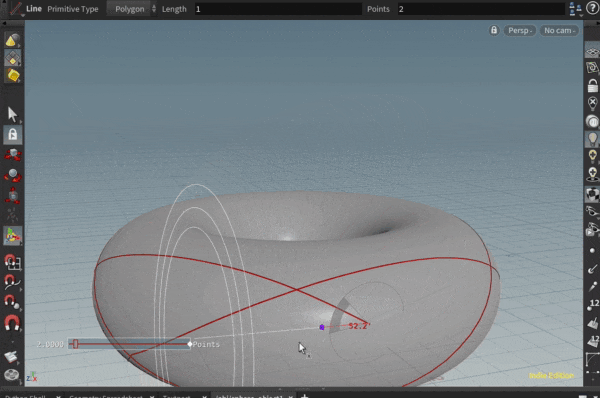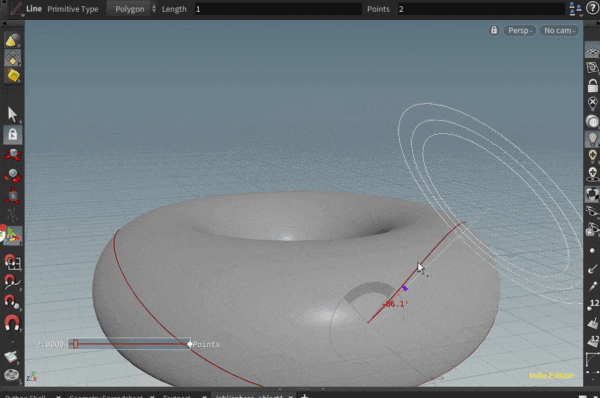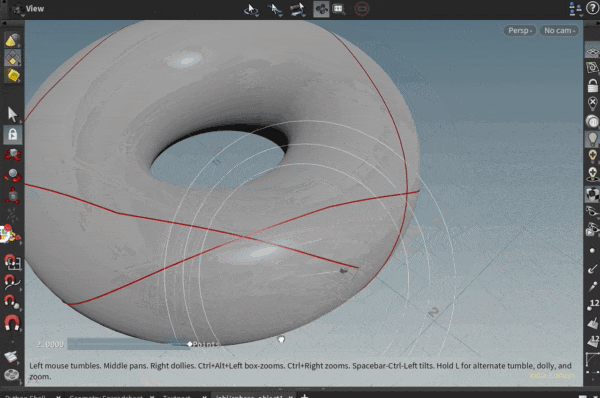
いくつかのポリゴンで測地線を引いてみた例が以下になります。
ポリゴンの角にあたってしまう場合に行き先を失っておかしくなる挙動を取り切れていませんが…
実際、トーラスの模型を作って指で撫でて見ると、トーラス上の測地線が上記の線のようになりそうだな、というのが感覚としてわかって面白いです。
測地線が引けるHIPファイルは以下に公開しておきます。
参考資料
正直数学的な部分は丁寧に解説をする能力も、しっかり理解する能力も持ち合わせていないので、
ちゃんとした形のものを勉強したい方は、
多様体の基礎のキソ
共変微分 - EMANの相対性理論 - EMANの物理学
情報幾何学の基礎(書籍)
などを参照していただけると助かります。
トーラスの測地線の解析解を解説しているPDF The Curvature and Geodesics of the Torus も参考になります。
おわりに
Houdiniを幾何学の勉強ツール・可視化ツールとして使うと、UIも使いやすく、割となんでも出来て、当然ながら我々Houdiniユーザーとしては学習コストがないのでとても便利です！
質問やここって間違ってるよね？ってところがあればTwitterやコメントで遠慮なくお願いします。